2022.3.31 图论——DIJKSTRA 算法

---

一、Prim 算法

参考文章

1.DIJKSTRA 算法简介

找了很多地方也讲不清，回去翻去年上课时的PPT了。

An example of a greedy algorithm; locally best choice is globally best. Doesn’t work if weights can be
negative.

DIJKSTRA 算法解决的是最短路径问题，给定一个图和图中某一节点，返回一个数组，数组中存储的是指定节点到所有其他节点的最短路径。

2.DIJKSTRA 算法流程

1. Maintain list S of visited nodes.
   

2. Choose an unvisited node 𝑢 with shortest 𝑆-path and
   put it to 𝑆.

3. Update distances (of remaining unvisited nodes) from
   starting node 𝑠 in case adding 𝑢 has established
   shorter paths.

4. Repeat.

①

②

③

④

⑤

3.实现代码

课内给的伪代码：

---

题解代码：

class State {
    // 图节点的 id
    int id;
    // 从 start 节点到当前节点的距离
    int distFromStart;

    State(int id, int distFromStart) {
        this.id = id;
        this.distFromStart = distFromStart;
    }
}

// 返回节点 from 到节点 to 之间的边的权重
int weight(int from, int to);

// 输入节点 s 返回 s 的相邻节点
List<Integer> adj(int s);

// 输入一幅图和一个起点 start，计算 start 到其他节点的最短距离
int[] dijkstra(int start, List<Integer>[] graph) {
    // 图中节点的个数
    int V = graph.length;
    // 记录最短路径的权重，你可以理解为 dp table
    // 定义：distTo[i] 的值就是节点 start 到达节点 i 的最短路径权重
    int[] distTo = new int[V];
    // 求最小值，所以 dp table 初始化为正无穷
    Arrays.fill(distTo, Integer.MAX_VALUE);
    // base case，start 到 start 的最短距离就是 0
    distTo[start] = 0;

    // 优先级队列，distFromStart 较小的排在前面
    Queue<State> pq = new PriorityQueue<>((a, b) -> {
        return a.distFromStart - b.distFromStart;
    });

    // 从起点 start 开始进行 BFS
    pq.offer(new State(start, 0));

    while (!pq.isEmpty()) {
        State curState = pq.poll();
        int curNodeID = curState.id;
        int curDistFromStart = curState.distFromStart;

        if (curDistFromStart > distTo[curNodeID]) {
            // 已经有一条更短的路径到达 curNode 节点了
            continue;
        }
        // 将 curNode 的相邻节点装入队列
        for (int nextNodeID : adj(curNodeID)) {
            // 看看从 curNode 达到 nextNode 的距离是否会更短
            int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);
            if (distTo[nextNodeID] > distToNextNode) {
                // 更新 dp table
                distTo[nextNodeID] = distToNextNode;
                // 将这个节点以及距离放入队列
                pq.offer(new State(nextNodeID, distToNextNode));
            }
        }
    }
    return distTo;
}

解释一下 State 类是怎么回事：
二叉树的层级遍历框架：

// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
    if (root == null) return 0;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    int depth = 1;
    // 从上到下遍历二叉树的每一层
    while (!q.isEmpty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            printf("节点 %s 在第 %s 层", cur, depth);

            // 将下一层节点放入队列
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
        depth++;
    }
}

我们去掉 while 循环里面的 for 循环并保持体现节点深度的变量（或指在必要时能返回节点深度的方法）：

class State {
    // 记录 node 节点的深度
    int depth;
    TreeNode node;

    State(TreeNode node, int depth) {
        this.depth = depth;
        this.node = node;
    }
}

// 输入一棵二叉树的根节点，遍历这棵二叉树所有节点
void levelTraverse(TreeNode root) {
    if (root == null) return 0;
    Queue<State> q = new LinkedList<>();
    q.offer(new State(root, 1));

    // 遍历二叉树的每一个节点
    while (!q.isEmpty()) {
        State cur = q.poll();
        TreeNode cur_node = cur.node;
        int cur_depth = cur.depth;
        printf("节点 %s 在第 %s 层", cur_node, cur_depth);

        // 将子节点放入队列
        if (cur_node.left != null) {
            q.offer(new State(cur_node.left, cur_depth + 1));
        }
        if (cur_node.right != null) {
            q.offer(new State(cur_node.right, cur_depth + 1));
        }
    }
}

以上，我们就可以不使用 for 循环也确切地知道每个二叉树节点的深度了。

二、例题

第一题：743. 网络延迟时间

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

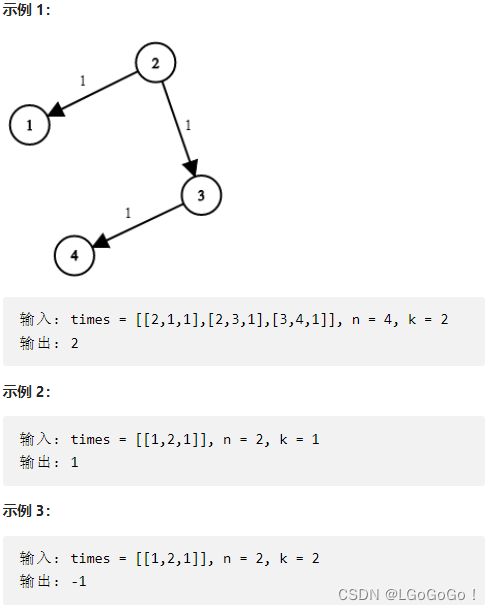
答案代码：

package Graph;

import java.util.*;

/**
 * @author: LYZ
 * @date: 2022/3/31 18:35
 * @description: 743. 网络延迟时间
 */
public class NetworkDelayTime {
    public static void main(String[] args) {
        NetworkDelayTime time = new NetworkDelayTime();
        int[][] times = {{2, 1, 1}, {2, 3, 1}, {3, 4, 1}};
        int ans = time.networkDelayTime(times, 4, 2);
        System.out.println(ans);
    }

    public int networkDelayTime(int[][] times, int n, int k) {
        // 节点编号是从 1 开始的，所以要一个大小为 n + 1 的邻接表
        List<int[]>[] graph = new LinkedList[n + 1];
        for (int i = 1; i <= n; i++) {
            graph[i] = new LinkedList<>();
        }
        // 构造图
        for (int[] edge : times) {
            int from = edge[0];
            int to = edge[1];
            int weight = edge[2];
            // from -> List<(to, weight)>
            // 邻接表存储图结构，同时存储权重信息
            // 这也是为什么 graph 的存储结构为 List<int[]>[]
            // graph 本身是一个数组，数组中是一个个邻接表（List集合），而在有权图中邻接表不仅要存边指向的节点，
            // 还要记录有向边的权值，从而List集合中存储的也是数组，且为整型数组
            graph[from].add(new int[]{to, weight});
        }
        // 启动 dijkstra 算法计算以节点 k 为起点到其他节点的最短路径
        int[] distTo = dijkstra(k, graph);

        // 找到最长的那一条最短路径
        int res = 0;
        for (int i = 1; i < distTo.length; i++) {
            if (distTo[i] == Integer.MAX_VALUE) {
                // 有节点不可达，返回 -1
                return -1;
            }
            res = Math.max(res, distTo[i]);
        }
        return res;
    }

    class State {
        // 图节点的 id
        int id;
        // 从 start 节点到当前节点的距离
        int distFromStart;

        State(int id, int distFromStart) {
            this.id = id;
            this.distFromStart = distFromStart;
        }
    }

    // 输入一个起点 start，计算从 start 到其他节点的最短距离
    int[] dijkstra(int start, List<int[]>[] graph) {
        // 定义：distTo[i] 的值就是起点 start 到达节点 i 的最短路径权重
        int[] distTo = new int[graph.length];
        Arrays.fill(distTo, Integer.MAX_VALUE);
        // base case，start 到 start 的最短距离就是 0
        distTo[start] = 0;

        // 优先级队列，distFromStart 较小的排在前面
        Queue<State> pq = new PriorityQueue<>((a, b) -> {
            return a.distFromStart - b.distFromStart;
        });
        // 从起点 start 开始进行 BFS
        pq.offer(new State(start, 0));

        while (!pq.isEmpty()) {
            State curState = pq.poll();
            int curNodeID = curState.id;
            int curDistFromStart = curState.distFromStart;

            if (curDistFromStart > distTo[curNodeID]) {
                continue;
            }

            // 将 curNode 的相邻节点装入队列
            for (int[] neighbor : graph[curNodeID]) {
                int nextNodeID = neighbor[0];
                int distToNextNode = distTo[curNodeID] + neighbor[1];
                // 更新 dp table
                if (distTo[nextNodeID] > distToNextNode) {
                    distTo[nextNodeID] = distToNextNode;
                    pq.offer(new State(nextNodeID, distToNextNode));
                }
            }
        }
        return distTo;
    }
}