2022.3.13 LeetCode —— 二叉树

---

一、今日刷题

1. 第七部分：二叉树 – 96. 不同的二叉搜索树

跳转LeetCode

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

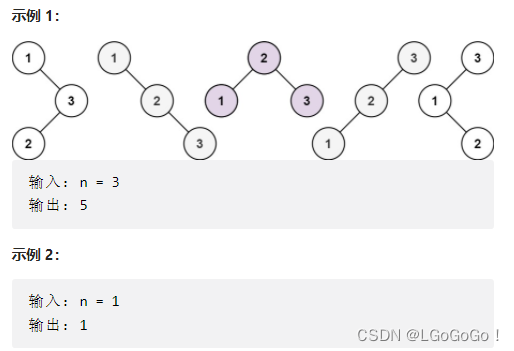
答案代码：

做题时并没有思路，根据题解，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种，就是看由 1 到 n 的值分别组成根节点，组成的树满足二叉搜索树结构总共由多少种可能。

根据 BST 的特性，根节点的左子树都比根节点的值小，右子树的值都比根节点的值大，所以如果固定3作为根节点，左子树节点就是{1,2}的组合，右子树就是{4,5}的组合。
左子树的组合数和右子树的组合数乘积就是3作为根节点时的 BST 个数。

基本代码：
时间复杂度很高，甚至提交超时了…

/* 主函数 */
int numTrees(int n) {
    // 计算闭区间 [1, n] 组成的 BST 个数
    return count(1, n);
}

/* 计算闭区间 [lo, hi] 组成的 BST 个数 */
int count(int lo, int hi) {
    // base case
    if (lo > hi) return 1;

    int res = 0;
    for (int i = lo; i <= hi; i++) {
        // i 的值作为根节点 root
        int left = count(lo, i - 1);
        int right = count(i + 1, hi);
        // 左右子树的组合数乘积是 BST 的总数
        res += left * right;
    }

    return res;
}

下面这句话不太理解：

注意 base case，显然当lo > hi闭区间[lo, hi]肯定是个空区间，也就对应着空节点 null，虽然是空节点，但是也是一种情况，所以要返回 1 而不能返回 0。

动态规划代码：

package BinaryTree.BinarSearchTree;

import java.util.Arrays;

/**
 * @author: LYZ
 * @date: 2022/3/13 15:42
 * @description: 96. 不同的二叉搜索树 给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。
 */
public class NumTrees {
    int[][] book;

    public int numTrees(int n) {
        book = new int[n + 1][n + 1];
        //Arrays.fill(book, 0);
        int ans = count(1, n);
        return ans;
    }

    int count(int left, int right) {
        if (left > right) {
            return 1; //为什么不能return 0;
        }
        if (book[left][right] != 0) {
            return book[left][right];
        }

        int ans = 0;
        for (int i = left; i <= right; i++) {
            int leftTree = count(left, i - 1);
            int rightTree = count(i + 1, right);
            ans += leftTree * rightTree;
        }
        book[left][right] = ans;
        return ans;
    }
}

2. 第七部分：二叉树 – 95. 不同的二叉搜索树 II

跳转LeetCode

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

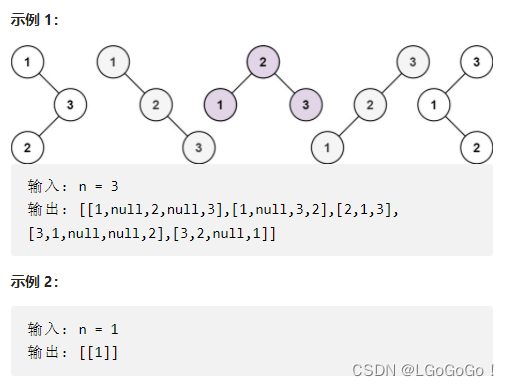
答案代码：

明白了上道题构造合法 BST 的方法，这道题的思路也是一样的：
1、穷举root节点的所有可能。
2、递归构造出左右子树的所有合法 BST。
3、给root节点穷举所有左右子树的组合。

package BinaryTree.BinarSearchTree;

import java.util.ArrayList;
import java.util.List;
import java.util.ListIterator;

/**
 * @author: LYZ
 * @date: 2022/3/13 16:05
 * @description: 95. 不同的二叉搜索树 II
 */
public class GenerateTrees {
    public List<TreeNode> generateTrees(int n) {
        return build(1, n);
    }

    List<TreeNode> build(int left, int right) {
        List<TreeNode> ans = new ArrayList<>();
        if (left > right) {
            ans.add(null);
            return ans;
        }

        for (int i = left; i <= right; i++) {
            List<TreeNode> leftTree = build(left, i - 1);
            List<TreeNode> rightTree = build(i + 1, right);
            //给 root 节点穷举所有左右子树的组合。
            for (TreeNode l : leftTree) {
                for (TreeNode r : rightTree) {
                    TreeNode root = new TreeNode(i);
                    root.left = l;
                    root.right = r;
                    ans.add(root);
                }
            }
        }
        return ans;
    }
}

总结

1.体会一下 base case 中的

if (left > right) {
	ans.add(null);
    return ans;
}

因为 i 的值是从 left 开始的，而下方的递归语句

List<TreeNode> leftTree = build(left, i - 1);
List<TreeNode> rightTree = build(i + 1, right);

是从 i - 1（即left - 1）开始的，这就会导致代码进入 base case，当然这符合常理，假设节点值为 1 ~ 5，在for循环的第一次执行中，以 1 为整棵二叉搜索树的根节点，当然没有左子树，但不要忽略了右子树。所以此时中断的只是左子树方面的递归，右子树的递归正常进行。

2.同理，参照第一题里的 base case，

if (left > right) {
	return 1; //为什么不能return 0;
}

疑问也就解开了，当左子树为空时，也属于满足条件的一种情况。而且我们 ans 的计算公式

ans += leftTree * rightTree;

若在 base case时 return 0，即令 leftTree = 0，最终的 ans 会一直为0，显然是不对的。