图像差分求导

最新推荐文章于 2025-10-19 21:05:34 发布

原创

最新推荐文章于 2025-10-19 21:05:34 发布 · 置顶 · 1.8k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#图像一阶导数

本文介绍了图像中像素点分布的概念，通过数字图像的二维数组表示，详细阐述了一阶导数的水平垂直差分计算方法，并探讨了如何处理图像边缘像素的梯度计算问题，提供了两种不同的补全策略。

1、理论依据

首先要知道图像中像素点的分布问题。数字图像中，f（x，y）可表示成一个M*N的二维数字阵列，即如下图

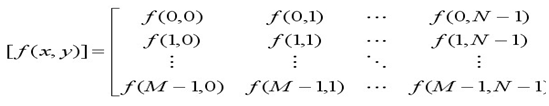
对于图像f（i,j），用差分来近似代替导数，则在点(i,j)处沿x方向和y方向的一阶差分可表示为：

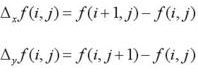
这种差分为水平垂直差分，在图像中表示如下图

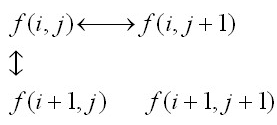
2、程序实现：

对于图像来说，通常图像中最右一列和最下一行的各像素的梯度无法求得。可以有两种方式补全：

1）用前一列和最后一列的差值补全水平查分的最后一列，第一行与最后一行的差值补垂直差分的最后一行。代码如下：

bool diffBackwards(Mat &src, Mat &dst, int selection)
{
    
    if (selection != 1 && selection != 2)
    {
        cout << "Input selection error" << endl;
        return false;
    }

    int dx, dy;
    switch (selection)
    {
        case 2:
            dx = 1;    dy = 0;//x方向微分
            break;
        case 1:
            dx = 0;    dy = 1;//y方向微分
         &nb