支持向量机算法学习笔记（二）

上节的支持向量机分类：

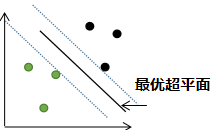
若存在异常点，用上节的支持向量机算法进行分类：

由上述分类结果可知，若存在异常点，用上节的支持向量机进行分类，泛化性能较差。

解决方法是给目标函数添加一个松弛变量，i表示样本编号。

目标函数：

约束条件：

其中惩罚参数C>0，C越大表示对误分类的惩罚越大。

最小化目标函数可以参考第一节，用拉格朗日函数将有约束的目标函数转换为无约束的目标函数，即：

其中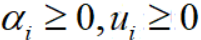

要优化的目标函数：

可转换为对偶问题：

令其偏导数等于0：

得：

利用上式得到的结果，代入目标函数，消除参数w和b，得：

最大化，约束条件为：

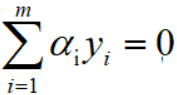
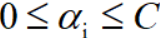
利用SMO算法求解。

后面的计算与支持向量机（一）一致，若得到的结果，通过下式

求得模型的参数w。

1）当 0<α<C时，所对应的样本落在分割边界上，即支持向量点。根据这些样本求解对应的参数b，有：

因此：

求所有满足α条件的样本参数b的平均值，若 0<α<C的样本共有M个，那么参数b的平均值为：

根据参数w和b，即可得最优分类超平面：

2）若α=0时，那么对应得样本已正确分类。

3）若α=C时，那么对应的样本有可能存在误分类得情况，这个需要看每个样本的松弛变量。

我们再来看目标函数的约束条件，根据KKT条件有：

上面的等式等价于样本点到超平面的距离为：

样本点到对应类别支持向量的距离为：

i) 若0<=<1，那么该样本点被正确分类，样本点所在位置是分类超平面与所属类别的间隔边界之间，如下图红色的样本点：

ii) =1时，该样本点所在的位置是最优超平面，无法被正确分类，如下图红色的样本点：

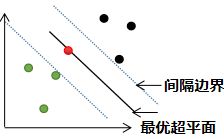
iii) >1时，该样本点所在的位置是所属另一个类的边界，如下图红色的样本点：

备注：红色样本点与黑色样本点所属相同的类。

欢迎扫码关注：