用Python求解线性规划（Scipy库）

在Python中，有很多库都提供了线性规划的求解方法，比如Scipy和cvxopt。现在先介绍Scipy的scipy.optimize模块求解线性规划问题。

Scipy中线性规划模型的标准形为

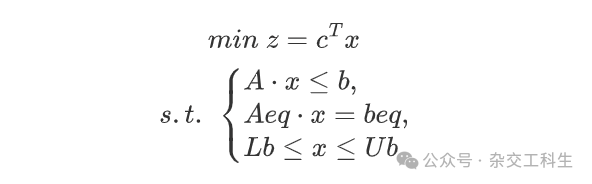
用linprog的基本调用格式为：

from scipy.optimize import linprogres=linprog(c,A,b,Aeq,beq)res=linprog(c,A=None,b=None,Aeq=None,beq=None,bounds=None,method='simplex')print(res.fun)print(res.x)

其中，

c：上述标准型中的模板向量；A，b：不等号约束；Aeq，beq：等号约束；bounds：决策向量的下界和上界所组成的n个元素的元组（bounds的默认取值是下界为0，上界为正无穷）。返回值res.x是求得的最优解；res.fun是目标幻术的最优解。

接下来让我们看看linprog函数的作用，在集成开发环境（IDLE）中先后输入：

from scipy.optimize import linproghelp(linprog)

就先不放输出了，那300多行看着操心，下次专门开讲一节如何看这些说明的好了，帮助你们快速入手。有兴趣的小伙伴可以输出看看。

接下来是几个实战的例子。

例如求解该式子的代码是：

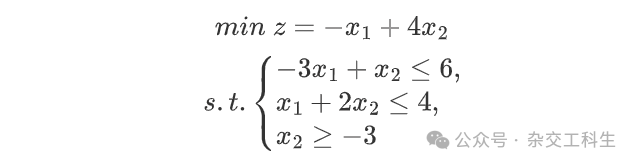
from scipy.optimize import linprog
c=[-1,4]
A=[[-1,1],[1,2]]
b=[6,4]
bounds=((None,None),(-3,None))
res=linprog(c,A,b,None,None,bounds)
print("res=\n",res)
print("\n\n")
print("目标数的最小值是：",res.fun)
print("最优解为",res.x)

输出：

res=
            con: array([], dtype=float64)
 crossover_nit: 0
         eqlin:  marginals: array([], dtype=float64)
  residual: array([], dtype=float64)
           fun: -22.0
       ineqlin:  marginals: array([-0., -1.])
  residual: array([19.,  0.])
         lower:  marginals: array([0., 6.])
  residual: array([inf,  0.])
       message: 'Optimization terminated successfully. (HiGHS Status 7: Optimal)'
           nit: 0
         slack: array([19.,  0.])
        status: 0
       success: True
         upper:  marginals: array([0., 0.])
  residual: array([inf, inf])
             x: array([10., -3.])

目标数的最小值是： -22.0最优解为 [10. -3.]

注意：该式子只能求最小值，且不等式约束只能是小于等于限制，所以要求最大值或存在大于等于约束时要在处理前转化一下。

例如：

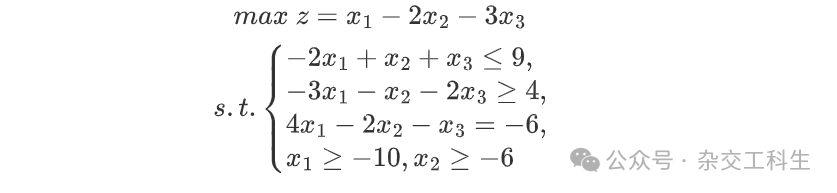
需转化为

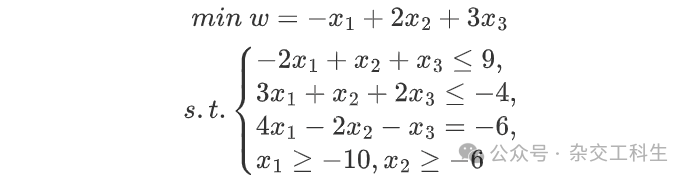
写出代码：

from scipy.optimize import linprog
c=[-1,2,3]
A=[[-2,1,1],[3,-1,-2]]
b=[9,-4]
Aeq=[[4,-2,-1]]
beq=[-6]
bounds=((-10,None),(0,None),(None,None))
res=linprog(c,A,b,Aeq,beq,bounds)
print("目标数的最小值是：",res.fun)
print("最优解为",res.x)

输出结果：

目标数的最小值是：0.399999999999999
最优解为 [-1.6  0.  -0.4]

接下来是cvxpy求解。

例题某种商品有6个仓库的存货量，8个客户的需求量，单位商品运价表如图。是确定6个仓库到8个用户的商品调运数量，使得总运费最小。

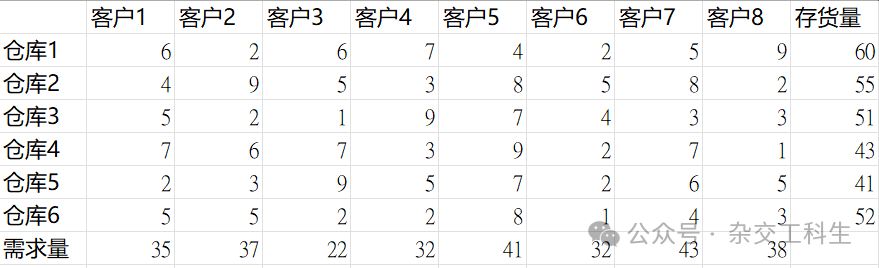
中间的表示单位运价

所以有线性规划模型：

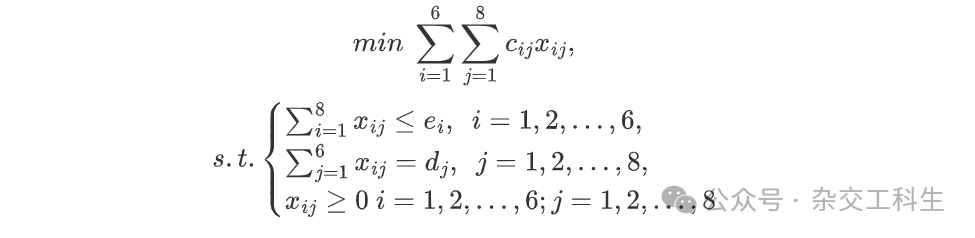
其中ei表示仓库的库存量；xij是从i到j的单价；ei是需求量

代码：

import cvxpy as cp
import numpy as np
import pandas as pd
d1=pd.read_excel("仓库.xlsx")
print(d1)
d2=d1.values
print(d2)
c=d2[:-1,:-1]
print(c)
d=d2[-1,:-1].reshape(1,-1)
print(d)
e=d2[:-1,-1].reshape(-1,1)
print(e)
x=cp.Variable((6,8))
obj=cp.Minimize(cp.sum(cp.multiply(c,x)))
con=[cp.sum(x,axis=1,keepdims=True)<=e,cp.sum(x,axis=0,keepdims=True)==d,x>=0]
prob=cp.Problem(obj,con)
prob.solve()
print("最优值：:",prob.value)
print("最优解:\n",prob.solve)