A tutorial on Principal Components Analysis - 主成分分析（PCA）教程

A tutorial on Principal Components Analysis

原著：Lindsay I Smith, A tutorial on Principal Components Analysis, February 26, 2002.

翻译：houchaoqun.
时间：2017/01/18.
出处：http://blog.youkuaiyun.com/houchaoqun_xmu  |  http://blog.youkuaiyun.com/Houchaoqun_XMU/article/details/54601984

说明：本文在翻译原文的过程中，在保证不改变原文意思的前提下，对一些知识点进行了扩充并附上参考网址。本人刚开始尝试翻译文献，经验不足，有些理解可能不到位，有些翻译可能不够准确。若读者们有发现有误之处，还望海涵并加以指正，本人会及时加以指正。

• 本文中涉及到公式的编辑，使用的是“在线LaTeX公式编辑器”，将编辑完成后的公式（图片的形式）复制到博文中即可。
• 原文可能缺少一些图，本人通过Matlab作图并补充。
• 本人在原文的基础上，额外提供了一些参考网址，有兴趣的读者们可以详细阅读。
• 为了更读者更深刻的理解PCA，本人还另外提供了案例，并用Matlab实现，仅供读者们参考。
• 为了更好的将理论运用到实际，本人打算在介绍完这篇PCA教程后，整理一篇基于PCA进行人脸识别的具体案例，由于水平有限，需要改正和完善的地方希望读者们提供宝贵的意见。

--------------------------------

主成分分析（PCA）教程

第1章：简介（Introduction）

    本教程的目的是为了让读者理解主成分分析（PCA）。PCA是一项很有用的统计学技术，已经应用在人脸识别（Face Recognition）和图像压缩（Image Compression）等领域，并且作为一项通用技术在高维数据中发现数据模型（降维技术）。

    开始介绍PCA之前，本教程首先介绍一些学习PCA相关的数学概念。包括，标准差，协方差，特征向量及其对应的特征值。这部分背景知识旨在使得PCA相关的章节更加简洁明了，如果读者对这部分的概念很熟悉，可以选择跳过这部分内容。

    本教程的一些相关案例旨在说明这些数学概念，让读者对这部分内容理解得更加深刻。如果读者想要更进一步的学习，“初等线性代数 第五版（Elementary Linear Algebra 5e）”这本数学工具书是一个很好的关于这些数学背景的资源。这本书的作者是Howard Anton，由John Wiley和Sons股份有限公司出版（国际标准图书编号[ISBN] 0-471-85223-6）。

 

第2章：数学背景（Background Mathematics）

    本章将给出一些对于理解PCA原理（涉及相关的推导过程）所需的基础数学技能。这部分知识都是相互独立的，并且都有相关的例子。理解为什么可能使用到这个技术以及在数据方面，某个操作的结果告诉了我们什么，比记住准确的数学技术更重要。虽然并不是这些技术都运用到PCA，但是最重要的技术（运用到PCA的技术）正是基于那些没有明确需要的技术（没有明确运用到PCA），所以对于初学者，还是有必要好好理解一下各个知识点。

    本章包含两大部分，第一部分介绍了关于统计学的知识，侧重于介绍数据（分布测量）是如何分布的（标准差，方差，协方差以及协方差矩阵）。第二部分介绍了矩阵代数，侧重于特征向量和特征值，矩阵的一些重要性质是理解PCA的基础。

2.1 统计学（Statistics）

    关于统计学的整个主题是围绕着你有一个大的数据集，并且你想要分析这个数据集中点跟点之间的关系。本章将侧重介绍一些读者能够亲自操作（手算验证）的测量指标（标准差，方差，协方差以及协方差矩阵），并且对于数据本身，这些测量指标告诉了我们什么（即，测量值反映数据的关系）。

2.1.1 标准差（Standard Deviation）

    为了理解标准差，我们需要一个数据集，统计学家通常使用来自总体（population）中的一个样本（sample）。此处使用选举投票（election polls）为例，“总体”是这个国家的所有人，而统计学家测量（measure）的样本是这个总体的一个子集。统计学的伟大之处在于仅仅通过测量（可以通过电话调查或者类似的方法）总体中的一个样本，就能够算出与总体最相似的测量结果（即，通过测量样本进而解决总体）。在统计学这个章节，作者假设本文使用的数据集是来自更大总体的样本（总体的数据集比样本的数据集更大）。（本章）下文有一个关于样本和总体更详细信息的参考网址。

    例如，对于数据集X：

    我们简单的使用符号X表示整个数据集。如果想表示数据集中的某个元素，可以使用下标表示指定的元素（值），如 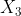  表示数据集X的第三个元素，对应的值是4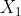；  指的是这个序列中的第一个元素，值为1；但是这里并没有像我们在一些教科书上提到的 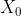（因为此处的下标从1开始）。此外，符号n表示数据集X的元素个数。

    我们可以对一组数据集进行很多种计算。例如，我们可以计算这个样本（数据集）的平均值（mean）。作者假设读者们理解样本X的均值的含义，此处仅给出计算公式，如下：

    注：符号 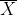  表示数据集X的均值。上述公式表示，“累加数据集X中的所有元素的值，然后除以元素总数n”。

   不幸的是，均值仅仅告诉我们数据集的中间点。例如，以下两组数据集具有相关的均值（mean = 10），但是这是两组完全不同的数据。

    因此，这两组数据集有什么不同呢？数据的分布不同。数据集的标准差反映了数据是如何分布的（个体间的离散程度）。

    我们要怎样计算标准差（Standard Deviation）呢？标准差（SD）的英文定义是，“The average distance from the mean of the data set to a point（数据集中每个点到均值的平均距离）”。标准差的计算方式是，首先计算每个点到样本均值的距离的平方，然后进行累加，最后将累加的结果除以 n-1 再开根号，如下公式所示：

    其中，通常使用s表示一个样本的标准差。读者可能会问，“为什么是除以 (n-1) ，而不是 n？”。答案有些复杂，但总的来说，如果你的数据集是样本数据集，也就是说如果你选择的是一个真实世界中的子集（例如，对样本数为500个人的选举投票案例进行测量），你就需要使用 (n-1) 。因为事实证明，对于样本，使用(n-1)得到的答案更接近于标准差的结果（如果你尝试使用Matlab提供的cov函数，也是除以n-1）。如果你处理的数据集是总体，那你应该使用n。（其他解释参考[ 点击进入链接 ]：如是总体，标准差公式根号内除以n，如是样本,标准差公式根号内除以（n-1)；这样能使我们以较小的样本集更好的逼近总体的标准差，即统计上所谓的“无偏估计”）。不管怎样，如果你计算的不是样本的标准差，而且总体的标准差，那么公式根号内应该除以n，而不是(n-1)。对于这部分内容，有意愿更进一步了解的读者可以参考网址：http://mathcentral.uregina.ca/RR/database/RR.09.95/weston2.html。这个网址用相似的方式介绍了标准差，还提供了一个实验案例，解释了标准差公式根号内的两种分母（即，n和n-1）的区别，并对“样本”和“总体”的区别进行了讨论。

    如下表2.1所示的两组数据，分别计算了它们的标准差。

   正如预期的，表2.1的第一部分的标准差（8.3266）更大是因为这组样本数据相对于均值的分布更离散。正如另一个例子所示，样本数据为[ 10 10 10 10 ]，均值同样为10，但是它的标准差为0。因为所有元素的值都一样，不存在偏离均值的元素。

2.1.2 方差（Variance）

    方差是另一种测量数据集离散程度的方式。实际上，方差和标准差几乎是相同的。公式如下：

    读者们可以发现方差仅仅是对标准差等式左右两边进行平方（方差的公式中没有对其开根号）。对于样本中的方差 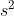  是常用的符号。这两个衡量值（方差和标准差）都是衡量数据的离散程度。标准差是最常用的衡量值，但方差同样适用。本文在介绍了标准差之外，还介绍方差的原因是为下一个章节的协方差提供基础（铺垫，抛砖引玉）。

    练习：如下三组数据集所示，分别求出均值，标准差和方差。

• [ 12 23 34 44 59 70 98 ]
• [ 12 15 25 27 32 88 89 ]
• [ 15 35 78 82 90 96 97 ]

2.1.3 协方差（Covariance）

    上述我们关注的两种（标准差和方差）测量指标的对象仅仅是一维数据集（局限性），比如房间里所有人的身高或者教师批改试卷等。然而，许多数据集都不只是一维，而且对于这些数据集，统计分析的目标通常是寻找这些维度之间是否存在任何关系。例如，我们将班级上所有学生的身高以及学生考试的分数作为数据集，然后使用统计分析方法去判断学生的身高是否对他们的分数有任何影响。

    标准差和方差仅仅处理一维数据，因此你只能分别对数据集中的每一维计算出标准差（每一维对应一个标准差）。然而，找到一种与上述相似，并且能够度量各个维度偏离其均值程度的测量指标是非常有用的。

    【协方差】就是这样的一种测量指标。协方差通常用来测量2维的数据集。如果你计算的协方差中的2个维度都是同一个变量，此时得到的就是方差。（协方差正常处理的是二维数据，维数大于2的时候，就用协方差矩阵表示）因此，如果有一组三维数据集（x, y, z），那么我们需要分别计算x维度和y维度，x维度和z维度，y维度和z维度的协方差。计算x维度和x维度，y维度和y维度，z维度和z维度的协方差就相当于分别计算x，y，z维度的方差（这就是两个维度都是同一个变量的情况）。

    协方差的公式和方差的公式很相似，方差的公式（度量各个维度偏离其均值的程度）如下所示：

    其中，作者仅仅是拓展了平方项变成两个部分（如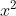，  表示成  *  ）。因此，协方差的公式如下：

    上述两个公式（方差和标准差）除了分子中的第二个括号内将X用Y代替以为，其他都一样。用英文定义就是，“For each data item, multiply the different between the x value and the mean of x, by the difference between the y value and the mean of y. Add all these up, and divide by (n -1)”（对于X和Y的每个数据项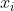，  与 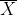（变量X的均值）的差乘以 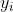  与 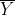 （变量Y的均值）的差，然后将它们累加起来后除以 (n-1) ）。

    那么，协方差是如何运作的呢？让我们使用一些实例数据。想象我们走进世界中，收集到一些二维数据。我们统计一群学生用在学习 COSC241 这个课程的时间（小时）以及他们获得的分数。现在我们有了二维的数据，第一维是H维，表示学生学习的时间（以小时为单位），第二维是M维，表示学生获得的分数。如下图所示，包含了我们刚刚想象的数据以及H和M之间的协方差 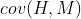 的计算结果。

图示：学生学习的时间H，获得的分数M

    那么，这些数据告诉我们什么？协方差的符号（正好或者负号）比数值更加重要。如果协方差的值是正数，表明这两维（H和M）是正相关，也就是说，随着学生学习的时间（H）的增加，学生获得的分数（M）也增加。如果值是负数，一个维度增加则另一个维度减小（数据呈负相关）。对于这个例子，如果协方差最终得到的结果是负值，也就是负相关，意味着随着学生学习时间的增加，学生获得的分数则减少。最后还有一种情况是，当协方差的值为0，意味着这两维（如，变量H和M）是相互独立的（不相关）。

    实验结果（上述数据）可以很直观的通过对原始数据作图，如下图所示，学生所得的分数M随着学生学习的时间H的增加而增加。然而，数据的可视化（作图）也仅仅局限于2维和3维的数据。因为对于任意2维的数据都可以计算协方差的值，因此这项技术（协方差）经常用于发现高维数据之间的关系（这些高维数据是很难进行可视化的）。