神经网络

神经网络

• 神经元模型
• BP算法

神经元模型

神经网络中最基本的单元是神经元模型（neuron）。常见的神经元模型为： M-P模型
其基本结构如下图所示：

神经元模型最理想的激活函数也是阶跃函数，即将神经元输入值与阈值的差值映射为输出值1或0，若差值大于零输出1，对应兴奋；若差值小于零则输出0，对应抑制。但阶跃函数不连续，不光滑，故在M-P神经元模型中，也采用Sigmoid函数来近似。

将神经元以一定的层次结构连接起来，就形成了神经网络，若下图所示：

我们可以用图比较形象的表示出神经网络的基本结构，但是核心的问题是我们如何用数学来抽象表示，以完成对该问题的建模，优化。
若神经网络的结构如下图所示：

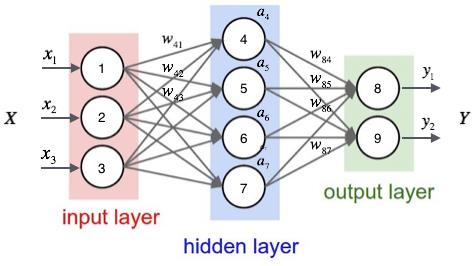
因为每一个节点都是一个神经元。有 Y=a*(W*X+b) a 是激活函数。w是权值，b是偏移量。 对于a4有如下：

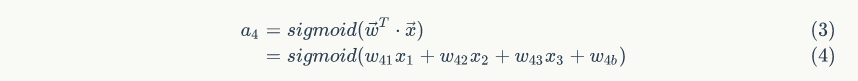
y1 有如下如下表达式：

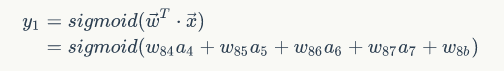
我们分层次表示该网络，并且采用向量的形式，则如下面的网络：

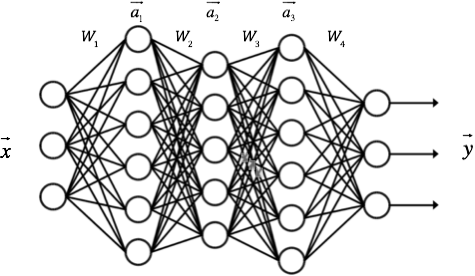
可表示为：

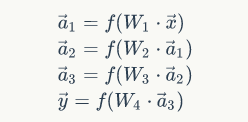
我们用数学的方式表示了该网络。核心的问题是，我们如何进行训练，训练过程中出现误差，我们又该怎么去优化。

BP 算法

假设，我们网络的激活函数为sigmoid ，则基于sigmoid 的网络的结构如下图所示：

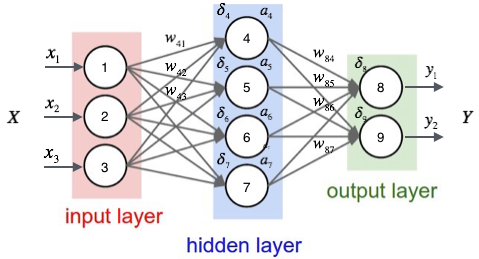
网络训练的过程简单描述是，我们给定网络的输入x 数据项，和label 数据y，核心是我们如何找到最优的权重w 。
我们的代价函数为：

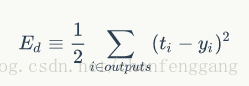
权重向量w 的迭代过程为：

观察上图，我们发现权重wji仅能通过影响节点j的输入值影响网络的其它部分（前面只能影响后面），设netj是节点j的加权输入，即

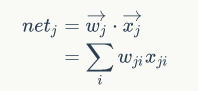
某个神经元的输出：

输出层权值训练：


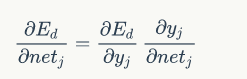
则：

有：

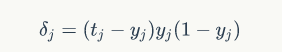
则输出层的方程为：

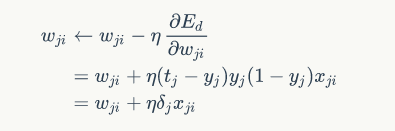
隐含层权值训练：


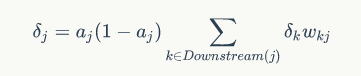
结论：

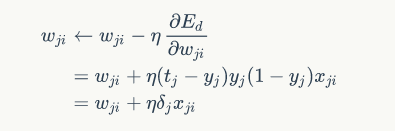
输出层：
隐含层：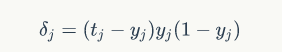

参考网址：
【1】：https://blog.youkuaiyun.com/chenfenggang/article/details/77542962