OBB盒的实现

制造几何仿真中的碰撞检测通常视为针对刚体对象间的碰撞检测，这样的话可以把非刚体即软体的建模和变形算法对碰撞检测的影响减少到最小。常见成熟的基于包围盒的碰撞检测（box intersection test）算法如：

1）沿坐标轴的包围盒AABB（axis-aligned bounding boxes）在碰撞检测的研究历史中使用得最久最广, 一个给定对象的AABB被定义为包含该对象且各边平行于坐标轴的最小的六面体。

AABB间的相交测试也比较简单，两个AABB相交当且仅当它们在三个坐标轴上的投影区间均重叠。定义AABB的六个最大最小值分别确定了它在三个坐标轴上的投影区间，因此AABB间的相交测试最多只需要六次比较运算。

2）包围球类似于AABB，也是简单性好紧密性差的一类包围盒，包围球被定义为包含该对象的最小的球体，计算给定对象E的包围球，首先需确定包围球的球心c，再由球心与三个最大值坐标所确定的点间的距离计算半径r。包围球的计算时间略多于AABB，但存储一个包围球只需两个浮点数。

3）方向包围盒OBB（oriented bounding box）是比较著名的一个包围盒类型。一个给定对象的OBB被定义为包含该对象且相对于坐标轴方向任意的最小的长方体。OBB最大特点是它的方向的任意性，这使得它可以根据被包围对象的形状特点尽可能紧密地包围对象，但同时也使得它的相交测试变得复杂。

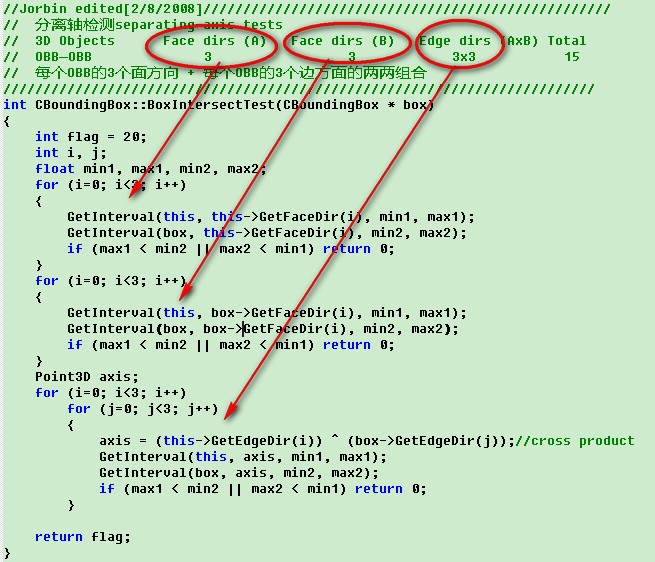
OBB间的相交测试基于分离轴理论（separating axis test）。若两个OBB在一条轴线上（不一定是坐标轴）上的投影不重叠，则这条轴称为分离轴。若一对OBB间存在一条分离轴，则可以判定这两个OBB不相交。对任何两个不相交的凸三维多面体，其分离轴要么垂直于任何一个多面体的某一个面，要么同时垂直于每个多面体的某一条边。因此，对一对OBB，只需测试15条可能是分离轴的轴（每个OBB的3个面方向再加上每个OBB的3个边方面的两两组合），只要找到一条这样的分离轴，就可以判定这两个OBB是不相交的，如果这15条轴都不能将这两个OBB分离，则它们是相交的。 

可以在运动过程中使用OBB进行初次碰撞检测，如果没有碰撞，则忽略进行下一个检测，如果发生碰撞，则调用更精细的碰撞检测。作者定义的包围盒（bounding box）和实现如下：

 

 

 

class Point3D 
{
public:
    double x;
    double y;
    double z;
public:
    Point3D();
    Point3D(double X, double Y, double Z);
    virtual ~Point3D();
public:
    //两个向量的交叉乘积（矩阵形式）用于就法向量
    Point3D operator^(Point3D pt);叉乘cross product
    Point3D operator-(Point3D pt);
    Point3D operator+(Point3D pt);
    double operator*(Point3D pt);//点乘dot product
    Point3D operator*(double k);
    void Normalize();
    float VecMod();
};

class CboundingBox
{
public:
    CBoundingBox();
    virtual ~CBoundingBox();
    void SetBendRelation(double bendDim, double dim, double cen[3]);
    void GetBoxCenter(double cen[3]);
    void GetMinMax(double* min_x, double* min_y, double* min_z, double* max_x, double* max_y, double* max_z);
    void TranslatedBox(double xOffset,double yOffset,double zOffset);
    void RotateBox(double angle, double x, double y, double z);
    void InitBoundingBox(Point3D Vertex[8]);
    void UpdateBoundingBox(Point3D Vertex[8]);//更新包围盒
public:
    //定义8个顶点，
    Point3D m_Vertex[8];
public:
    //Jorbin edited[2/8/2008]
    int BoxIntersectTest(CBoundingBox * box);
    void GetInterval(CBoundingBox * box, Point3D axis, float &min, float &max);
    float Dot(Point3D axis, Point3D pt);
    Point3D GetFaceDir(int indexID);   //取面方向
    Point3D GetEdgeDir(int indexID); //取边方向
}；

//点在该轴上投影值
float CBoundingBox::Dot(Point3D axis, Point3D pt)
{
    return (float)((axis * pt) / axis.VecMod());
}
void CBoundingBox::GetInterval(CBoundingBox * box, Point3D axis, float &min, float &max) 
{
    float value;
    min = max = Dot(axis, box->m_Vertex[0]);
    for(int i=1; i<8; i++)
    {
        value = Dot(axis, box->m_Vertex[i]);
        min = Min(min, value);
        max = Max(max, value);
    }
}

Point3D CBoundingBox::GetEdgeDir(int indexID)
{
    Point3D pt;
    Line3D tmpLine;
    switch(indexID) 
    {
        case 0://edge in parallel with x axis
            pt = tmpLine.Normalize(m_Vertex[0]), m_Vertex[1]);
            break;
        case 1://edge in parallel with y axis
            pt = tmpLine.Normalize(m_Vertex[0], m_Vertex[4]);
            break;
        case 2://edge in parallel with z axis
            pt = tmpLine.Normalize(m_Vertex[0], m_Vertex[3]);
            break;
    }
    return pt;
}
\

 

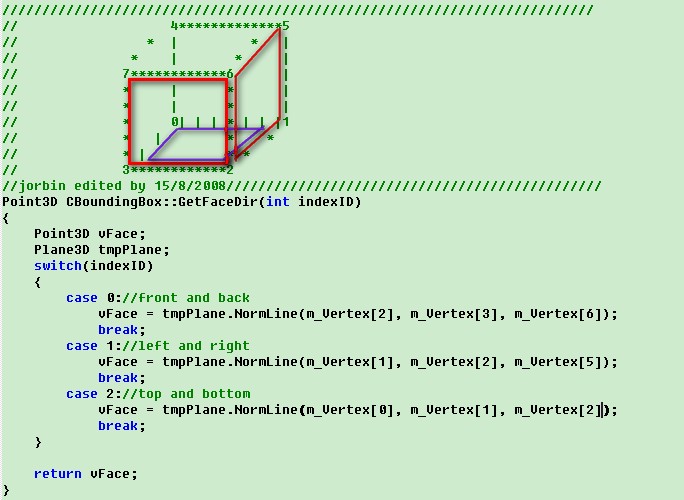
Point3D CBoundingBox::GetFaceDir(int indexID) {
    Point3D vFace;
    Plane3D tmpPlane;
    switch(indexID)
    {
        case 0://front and back
            vFace = tmpPlane.NormLine((m_Vertex[2], m_Vertex[3], m_Vertex[6]);
            break;
        case 1://left and right
            vFace = tmpPlane.NormLine((m_Vertex[1], m_Vertex[2], m_Vertex[5]);
            break;
        case 2://top and bottom
            vFace = tmpPlane.NormLine((m_Vertex[0], m_Vertex[1], m_Vertex[2]);
            break;
    }

    return vFace;
}

 

int CBoundingBox::BoxIntersectTest(CBoundingBox * box)
{
    int flag = 20;
    int i, j;
    float min1, max1, min2, max2;
    for (i=0; i<3; i++)
    {             
        GetInterval(this, this->GetFaceDir(i), min1, max1);              
        GetInterval(box, this->GetFaceDir(i), min2, max2);              
        if (max1 < min2 || max2 < min1) return 0;               
    } 
    for (i=0; i<3; i++)
    {             
        GetInterval(this, box->GetFaceDir(i), min1, max1);              
        GetInterval(box, box->GetFaceDir(i), min2, max2);              
        if (max1 < min2 || max2 < min1)    return 0;             
    }
    Point3D axis;
    for (i=0; i<3; i++)            
        for (j=0; j<3; j++) 
        {         
            axis = (this->GetEdgeDir(i)) ^ (box->GetEdgeDir(j));//cross product
            GetInterval(this, axis, min1, max1);                      
            GetInterval(box, axis, min2, max2);                      
            if (max1 < min2 || max2 < min1)    return 0;            
        }
    return flag;
} 

 

参考文献：
魏迎梅. 虚拟环境中碰撞检测问题的研究. 工学博士学位论文. 国防科学技术大学. 2000.10
申玉斌，蔡勇，华才建. 虚拟环境中的碰撞检测技术的研究与应用. 交通与计算机.2005.1
吴强，基于OBB碰撞检测算法的研究.硕士学位论文. 郑州大学.2007
http://www.gamasutra.com/features/19991018/Gomez_1.htm
http://www.gamasutra.com/features/19991018/Gomez_2.htm
http://www.gamasutra.com/features/19991018/Gomez_5.htm

转载于:https://www.cnblogs.com/jast/p/4100362.html