1、xgboost流程
2、如何求每一步的分类回归树?
3、xgboost损失函数
4、xgboost特点
5、xgboost与GBDT
6、xgboost调参
1、xgboost流程
1、初始化:估计是结构损失函数极小化的分类器;
2、添加回归树:
求使得损失函数$L_{m}=\sum_{i=1}^{N}(y_{i}-(\widehat{y_{i}}^{t-1}+f_{m}(x_{i})))^{2}+\sum_{k=1}^{m}\Omega (f_{k})$最小的回归树fm;
**这里的损失函数是结构损失,GBDT用的经验损失;
**这里还是一个集成学习的概念,每次走一小步逐渐逼近结果;
训练模型,直至误差小于要求,或树的个数为M时;
3、输出回归模型;
2、如何求每一步的分类回归树?
方法:贪心策略+最优化(牛顿法)
目标:1)确定树的模型结构;2)确定树模型的子节点输出;
流程:
1)对结构风险函数进行二阶泰勒展开;
$f(x+\delta )\approx f(x)+{f}'(x)\delta +\frac{1}{2}{f}''(x)\delta ^{2}$
**目标是求$\delta$,即对应的是CART的叶结点的值;
**这是运用牛顿迭代法来进行最优化,一次只逼近一小步;
**为什么这里可以用牛顿法呢?1)其他模型里Hesse矩阵不好求得问题这不存在,因为在xgboost里一个变量只与一个参数有关,与其他参数无关,Hesse矩阵好求;2)损失函数是二次项的形式,使得参数$\delta $也很好算;
**为什么用二阶泰勒展开呢?1)这是牛顿迭代的应用;2)效果是二阶泰勒展开是能够让自定义损失函数;在GBDT里,损失函数为平方误差,绝对值误差时,叶结点的值还比较好算,但是其他损失函数就很难计算,往往采用近似值;而二阶泰勒展开使最终的目标函数(叶结点的值)只依赖于数据点的在误差函数上的一阶导数和二阶导数,扩大了损失函数的适用范围;
2)损失函数的化简;
$$L_{t}=\sum_{j=1}^{J}[G_{tj}\omega_{tj}+\frac{1}{2}(H_{tj}+\lambda )\omega_{tj}^{2}]+\gamma J$$
3-1)用贪婪策略确定树的结构,即当前叶结点是否需要切分;
3-2)确定叶结点的值;
**GBDT的这两部是分开的,先确定树的结构,在确定叶结点的值;而xgboosr这两个步骤是合在一起的;
求$\delta$,即$\omega_{tj}$,对损失函数求导=0,得到$w_{tj} = - \frac{G_{tj}}{H_{tj} + \lambda}$;
则当$w_{tj}$取最优值时,损失函数为:$L_{t} = -\frac{1}{2}\sum_{j=1}^{J}\frac{G_{tj}^2}{H_{tj} + \lambda} +\gamma J$;
判断对于单个结点是否需要切分,以及如何切分,通常CART树衡量标准为基尼指数和均方误差,这里采用是损失函数降低最多为标准,即求$-\frac{1}{2}\frac{(G_{L}+G_{R})^2}{(H_{L} +H_{R})+ \lambda} +\gamma -( -\frac{1}{2}\frac{G_{L}^2}{H_{L} + \lambda} +\gamma -\frac{1}{2}\frac{G_{R}^2}{H_{R} + \lambda} +\gamma )$的最大值;
即$\frac{1}{2}\frac{G_{L}^2}{H_{L} + \lambda} +\frac{1}{2}\frac{G_{R}^2}{H_{R} + \lambda} -\frac{1}{2}\frac{(G_{L}+G_{R})^2}{(H_{L} +H_{R})+ \lambda}-\gamma $
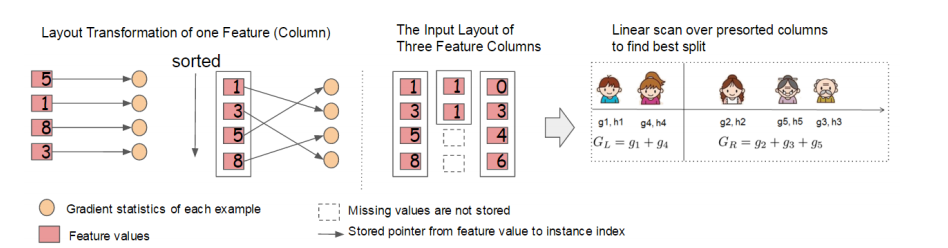
遍历每个特征的每个切分点,找到使损失函数降低最多得一个切分;
**这里就是并行提速的地方,无论怎么切分,$g_{tj}$和$h_{tj}$是不变的,只与当前变量相关;

3、xgboost损失函数
$L=\sum_{i=1}^{N}l(y_{i},\widehat{y_{i}})+\sum_{k=1}^{m}\Omega(f_{k})$
其中,
$\sum_{i=1}^{N}l(y_{i},\widehat{y_{i}})$为经验风险;
$\Omega(f)=\gamma J+\frac{1}{2}\lambda \sum_{j=1}^{J}\omega_{j}^{2}$为正则化项;
$L_{t}=\sum_{i=1}^{N}l(y_{i},\widehat{y_{i}}^{t-1}+f_{t}(x_{i})))+\sum_{k=1}^{t}\Omega (f_{k})$
对损失函数进行二阶泰勒展开:
$L_{t}\approx \sum_{i=1}^{N}\left (l(y_{i},\widehat{y_{i}}^{t-1})+\frac{\partial l(y_{i},\widehat{y_{i}}^{t-1})}{\partial \widehat{y_{i}}^{t-1}}f_{t}(x_{i})+\frac{1}{2} \frac{\partial^{2} l(y_{i},\widehat{y_{i}}^{t-1})}{\partial^{2} \widehat{y_{i}}^{t-1}}f_{t}^{2}(x_{i})\right )+\sum_{k=1}^{t}\Omega (f_{k})$
第t个弱学习器的一阶和二阶导数分别记为:
$g_{ti}=\frac{\partial l(y_{i},\widehat{y_{i}}^{t-1})}{\partial \widehat{y_{i}}^{t-1}}$,$ h_{ti}=\frac{\partial^{2} l(y_{i},\widehat{y_{i}}^{t-1})}{\partial^{2} \widehat{y_{i}}^{t-1}}$
则损失函数现在可以表达为:
$L_{t}\approx \sum_{i=1}^{N}\left (l(y_{i},\widehat{y_{i}}^{t-1})+g_{ti}f_{t}(x_{i})+\frac{1}{2} h_{ti}f_{t}^{2}(x_{i})\right )+\sum_{k=1}^{t-1}\Omega (f_{k})+\gamma J+\frac{1}{2}\lambda \sum_{j=1}^{J}\omega_{tj}^{2}$
损失函数里面$l(y_{i},\widehat{y_{i}}^{t-1})$和$\sum_{k=1}^{t-1}\Omega (f_{k})$为常数,对最小化结果无影响,去掉:
$L_{t}= \sum_{i=1}^{N}\left (g_{ti}f_{t}(x_{i})+\frac{1}{2} h_{ti}f_{t}^{2}(x_{i})\right )+\gamma J+\frac{1}{2}\lambda \sum_{j=1}^{J}\omega_{tj}^{2}$
将$w_{tj}$是第t个决策树中第j个叶结点(共J个叶结点)的取值,带入损失函数:
$L_{t}\approx \sum_{i=1}^{N}\left (g_{ti}\omega_{tj}+\frac{1}{2} h_{ti}\omega_{tj}^{2}\right )+\gamma J+\frac{1}{2}\lambda \sum_{j=1}^{J}\omega_{tj}^{2}$
由于第j个叶结点都取同一个$w_{tj}$,则损失函数为:
$L_{t}\approx \sum_{j=1}^{J}\left (\sum_{x_{i}\subset R_{tj}}^{}g_{ti}\omega_{tj}+\sum_{x_{i}\subset R_{tj}}^{}\frac{1}{2} h_{ti}\omega_{tj}^{2}\right )+\gamma J+\frac{1}{2}\lambda \sum_{j=1}^{J}\omega_{tj}^{2}$
$L_{t}\approx \sum_{j=1}^{J}[(\sum_{x_{i}\subset R_{tj}}^{}g_{ti})\omega_{tj}+\frac{1}{2}(\sum_{x_{i}\subset R_{tj}}^{} h_{ti}+\lambda )\omega_{tj}^{2}]+\gamma J$
令$G_{tj}=\sum_{x_{i}\subset R_{tj}}^{}g_{ti}$,$H_{tj}=\sum_{x_{i}\subset R_{tj}}^{} h_{ti}$,
则损失函数为:
$L_{t}=\sum_{j=1}^{J}[G_{tj}\omega_{tj}+\frac{1}{2}(H_{tj}+\lambda )\omega_{tj}^{2}]+\gamma J$
4、xgboost特点
xgboost支持子采样,不放回的抽样;
xgboost可以在训练过程中给出各个特征的评分,从而表明每个特征对模型训练的重要性,从而选出最优特征;评分标准有三个:
1.importance_type=weight(默认值),特征在所有树中作为划分属性的次数。
2.importance_type=gain,特征作为划分属性时loss平均的降低量。
3.importance_type=cover,特征在作为划分属性时对样本的覆盖度,即划分前叶结点的样本数。
XGBoost没有假设缺失值一定进入左子树还是右子树,则是尝试将所有缺失值在当前节点是进入左子树,还是进入右子树计算损失函数,更优来决定一个处理缺失值默认的方向,这样处理起来更加的灵活和合理。如果训练中没有数据缺失,预测时出现了数据缺失,那么默认被分类到右子树。
数据不需要归一化,特征的作用只是用来分裂结点,叶结点的值与特征值大小无关,是否归一化并不影响叶结点值的大小,也不影响梯度下降的进程;
多分类问题处理方法和GBDT一样;
5、xgboost与GBDT
1)xgboost是GBDT算法的高效实现;
2)xgboost加入了正则化项,提高了泛化能力;
3)GBDT对代价函数只做了一阶泰勒展开,使用了一阶导数信息;而xgboost对代价函数做了二阶泰勒展开,同时使用了一阶和二阶导数,更加准确;
4)传统GBDT一般用CART做基分类器,xgboost支持多种类型的分类器,如线性分类器;
5)传统GBDT每轮迭代使用全部数据,xgboost支持子采样;GBDT也可以支持了;
6)传统GBDT没有对缺失值进行处理,xgboost自动学习出缺失值处理策略;
6、xgboost调参
https://www.cnblogs.com/pinard/p/11114748.html
XGBoost的类库参数主要包括boosting框架参数,弱学习器参数以及其他参数。
6.1 XGBoost框架参数
对于XGBoost的框架参数,最重要的是3个参数: booster,n_estimators和objectve。
1) booster决定了XGBoost使用的弱学习器类型,可以是默认的gbtree, 也就是CART决策树,还可以是线性弱学习器gblinear以及DART。一般来说,我们使用gbtree就可以了,不需要调参。
2) n_estimators则是非常重要的要调的参数,它关系到我们XGBoost模型的复杂度,因为它代表了我们决策树弱学习器的个数。这个参数对应sklearn GBDT的n_estimators。n_estimators太小,容易欠拟合,n_estimators太大,模型会过于复杂,一般需要调参选择一个适中的数值。
3) objective代表了我们要解决的问题是分类还是回归,或其他问题,以及对应的损失函数。具体可以取的值很多,一般我们只关心在分类和回归的时候使用的参数。
在回归问题objective一般使用reg:squarederror ,即MSE均方误差。二分类问题一般使用binary:logistic, 多分类问题一般使用multi:softmax。
3.2 XGBoost 弱学习器参数
这里我们只讨论使用gbtree默认弱学习器的参数。 要调参的参数主要是决策树的相关参数如下:
1) max_depth: 控制树结构的深度,数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,需要限制这个最大深度,具体的取值一般要网格搜索调参。这个参数对应sklearn GBDT的max_depth。
2) min_child_weight: 最小的子节点权重阈值,如果某个树节点的权重小于这个阈值,则不会再分裂子树,即这个树节点就是叶子节点。这里树节点的权重使用的是该节点所有样本的二阶导数的和,即XGBoost原理篇里面的HtjHtj:
这个值需要网格搜索寻找最优值,在sklearn GBDT里面,没有完全对应的参数,不过min_samples_split从另一个角度起到了阈值限制。
3) gamma: XGBoost的决策树分裂所带来的损失减小阈值。也就是我们在尝试树结构分裂时,会尝试最大数下式:
这个最大化后的值需要大于我们的gamma,才能继续分裂子树。这个值也需要网格搜索寻找最优值。
4) subsample: 子采样参数,这个也是不放回抽样,和sklearn GBDT的subsample作用一样。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。初期可以取值1,如果发现过拟合后可以网格搜索调参找一个相对小一些的值。
5) colsample_bytree/colsample_bylevel/colsample_bynode: 这三个参数都是用于特征采样的,默认都是不做采样,即使用所有的特征建立决策树。colsample_bytree控制整棵树的特征采样比例,colsample_bylevel控制某一层的特征采样比例,而colsample_bynode控制某一个树节点的特征采样比例。比如我们一共64个特征,则假设colsample_bytree,colsample_bylevel和colsample_bynode都是0.5,则某一个树节点分裂时会随机采样8个特征来尝试分裂子树。
6) reg_alpha/reg_lambda: 这2个是XGBoost的正则化参数。reg_alpha是L1正则化系数,reg_lambda是L1正则化系数,在原理篇里我们讨论了XGBoost的正则化损失项部分:
上面这些参数都是需要调参的,不过一般先调max_depth,min_child_weight和gamma。如果发现有过拟合的情况下,再尝试调后面几个参数。
3.3 XGBoost 其他参数
XGBoost还有一些其他的参数需要注意,主要是learning_rate。
learning_rate控制每个弱学习器的权重缩减系数,和sklearn GBDT的learning_rate类似,较小的learning_rate意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。所以这两个参数n_estimators和learning_rate要一起调参才有效果。当然也可以先固定一个learning_rate ,然后调完n_estimators,再调完其他所有参数后,最后再来调learning_rate和n_estimators。























 6808
6808

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








