立体角介绍

最新推荐文章于 2022-11-14 20:30:32 发布

原创最新推荐文章于 2022-11-14 20:30:32 发布 · 793 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#微积分

formula 专栏收录该内容

5 篇文章

订阅专栏

这篇博客通过图像解释了立体角的概念，以直观的方式展示了如何从单位面积推导到单位立体角。博主首先介绍了l1和l2的计算，然后利用这些表达式导出了单位面积dA的公式，接着推导出单位立体角dΩ的表达式，并最终通过积分计算得出立体角Ω的公式，即Ω=4πsin²(θ/2)。

问题：
我读文献的时候，看到了朗伯平面的概念，于是就引出了立体角的概念。
描述：
网上许多博文就介绍了立体角，都缺乏直观的理解。于是我打算给出图像的手段，来直观的理解立体角。
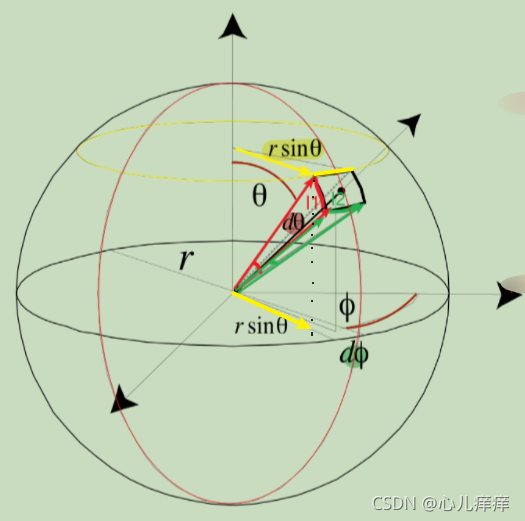
在这里插入图片描述
求单位面积 $d_A$ ，先从求 $l_1$ 和 $l_2$ 入手，并把投影的那一小块看作长方形。
$l1=r1×θ=r×dθ=rdϕl_1=r_1 \times \theta=r \times d_\theta=rd_\phi$
$l2=r2×θ=r×sin⁡θ⏟r2×dϕ=rsinθdϕl_2=r_2 \times \theta=\underbrace{\boxed{r \times \sin\theta}}_{r_2} \times d_\phi=rsin\theta d_\phi$
$⇒\Rightarrow$ $单位面积：\text{单位面积：}$ $dA=l1×l2=r2sin⁡θdθdϕd_A=l_1 \times l_2=r^2\sin\theta d_\theta d_\phi$
$⇒\Rightarrow$ $单位立体角：\text{单位立体角：}$ $dΩ=dAr2=r2sin⁡θdθdϕr2=sin⁡θdθdϕd_\Omega=\frac{d_A}{r^2}=\frac{\sout{r^2} \sin\theta d_\theta d\phi}{\sout{r^2}}=\sin\theta d_\theta d_\phi$
$∴Ω=∬Σsin⁡θdθdϕ=∫02π∫0θsin⁡θdθdϕ=∫02π(−cos⁡θ∣0θ)dϕ=∫02π[−cos⁡θ+1]dϕ=2π(1−cos⁡θ)=4πsin⁡2θ2\therefore \Omega=\iint_{\Sigma} \sin\theta d_\theta d_\phi =\int_0^{2\pi}\int_0^\theta \sin\theta d_\theta d_\phi = \int_0^{2\pi} ( -\cos\theta \bigg|_0^{\theta})d_\phi=\int_0^{2\pi}[-\cos\theta+1] d_\phi=2\pi(1-\cos\theta)=4\pi\sin^2\frac{\theta}{2}$