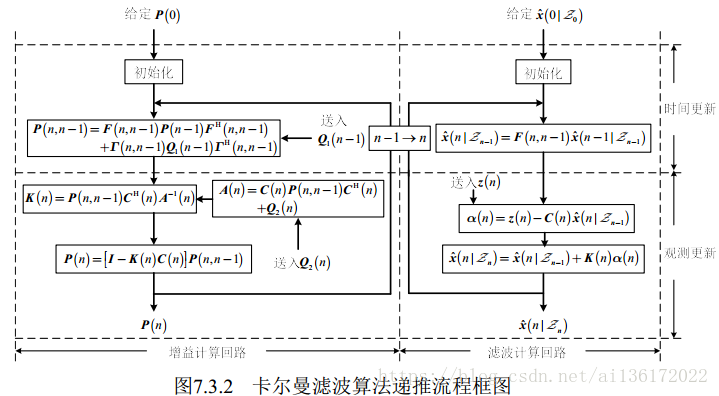
卡尔曼滤波在维纳滤波中的应用
- 考虑到最优权值是一个常值向量,因此状态方程为w(n)=w(n-1)
- 观测方程就是由滤波器的最优滤波误差推导出:d(n)=uT(n)w*(n)+e(n)
- 然后对应到观测方程和状态方程
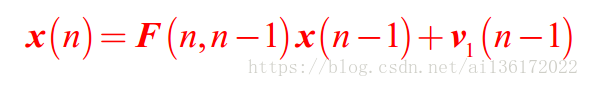
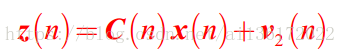
- 仿真时的权向量初始值为[0 0]T,估计误差相关矩阵P的初始值为I;
假设信号u(n)由一个四阶AR模型产生:u(n)-1.6u(n-1)+1.46u(n-2)-0.616u(n-3)+0.1525u(n-4)=v(n)
以该序列作为输入的四阶线性预测模型,用卡尔曼滤波估计该模型的最优权值;四阶线性预测模型要估计4个权值;且最终的权值应该和表达式的4个系数要接近。
clc,clear all,close all
for num=1:100
%% 产生给定方差的高斯白噪声
N=3000;
gv=0.0332;
v=rand(1,N)*sqrt(gv);
%% 给定 AR 模型产生 u(n)序列
a1=-1.6;
a2=1.46;
a3=-0.616;
a4=0.1525;
u(1)=0;u(2)=0;u(3)=0;u(4)=0;
for i=1:(N-4)
u(i+4)=-a1*u(i+3)-a2*u(i+2)-a3*u(i+1)-a4*u(i)+v(i+4);
end
%% 卡尔曼滤波
N2=2000;
Jmin=0.005;
for i=5:N2
U(:,i)=[u(i-1);u(i-2);u(i-3);u(i-4)];
end
P_esti=diag([1,1,1,1]);
W_esti=zeros(4,N2);
for l=1:N2
P_pre=P_esti;
A=(U(:,l))'*P_pre*U(:,l)+Jmin;
K=P_pre*U(:,l)/A;
alpha(l)=u(l)-(U(:,l))'*W_esti(:,l);
W_esti(:,l+1)=W_esti(:,l)+K*alpha(l);
P_esti=P_pre-K*(U(:,l))'*P_pre;
epsilon=W_esti(:,l+1)-W_esti(:,l);
MSE(l)=(W_esti(:,l+1)-W_esti(:,l))'*(W_esti(:,l+1)-W_esti(:,l));
end
% figure,plot(1:N2+1,W_esti) %单次W_estisum(:,:,num)=W_esti;
MSEsum(:,:,num)=MSE;
end
wmean=mean(W_estisum,3);
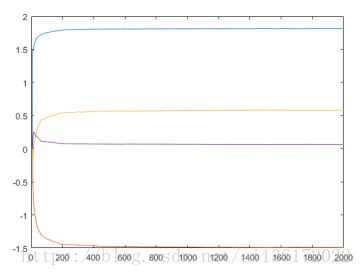
figure,plot(1:N2+1,wmean)
MSEmean=mean(MSEsum,3);
figure,plot(1:N2,MSEmean)单次实验的权向量迭代结果和100次独立实验求平均的权向量迭代结果:
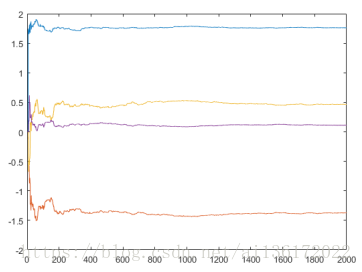
均方误差变化曲线:
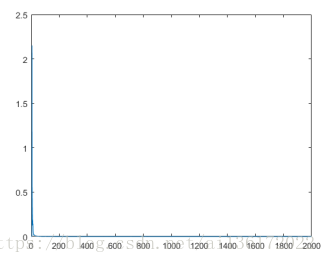





 本文通过仿真演示了卡尔曼滤波器在四阶自回归(AR)模型中的应用,目标是估计模型的最优权值。使用给定的AR模型参数生成输入序列,并通过卡尔曼滤波迭代估计权值,最终展示了权值迭代结果及其均方误差的变化。
本文通过仿真演示了卡尔曼滤波器在四阶自回归(AR)模型中的应用,目标是估计模型的最优权值。使用给定的AR模型参数生成输入序列,并通过卡尔曼滤波迭代估计权值,最终展示了权值迭代结果及其均方误差的变化。
















 1211
1211

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








