【强化学习】《强化学习的数学原理》知识总结与思考（一）基本概念

八宝粥行动

已于 2025-06-13 09:45:04 修改

阅读量1.1k

点赞数 14

CC 4.0 BY-SA版权

文章标签：学习笔记强化学习 QL 高等数学

于 2025-05-25 18:22:03 首次发布

本文链接：https://blog.youkuaiyun.com/agentssl/article/details/148121271

写在前面的话

本系列专栏是结合赵世钰老师的《强化学习的数学原理》的知识梳理与总结。总结不是对书本内容简单的堆砌，一定要加入自己的思考。希望大家通过我的笔记学到知识，欢迎在评论区讨论补充。不仅让自己对知识进行巩固强化，也能让粉丝看懂，创建本专栏的目的就达到了。

第一章基本概念

这一章主要以网格世界（grid world）为例介绍基本概念，之后引出马尔可夫决策过程（Markov decision process，MDP）的框架，为后面的学习打下基础。

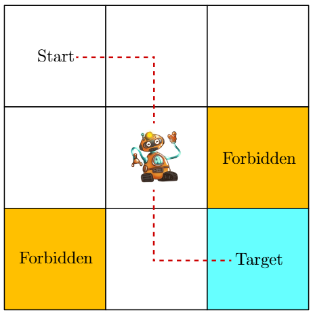
世界网格例子

如下图所示，智能体（agent）通过在网格中移动，需要避开禁区（黄色单元格），进入目标区域（蓝色单元格），我们设定规则如下：

每个时刻智能体只能占据一个单元格且只能上下左右或不动。
允许智能体进入禁区，但会受到惩罚。
若智能体试图越过网格世界的边界，则智能体在下一时刻会被弹回到原来的状态。

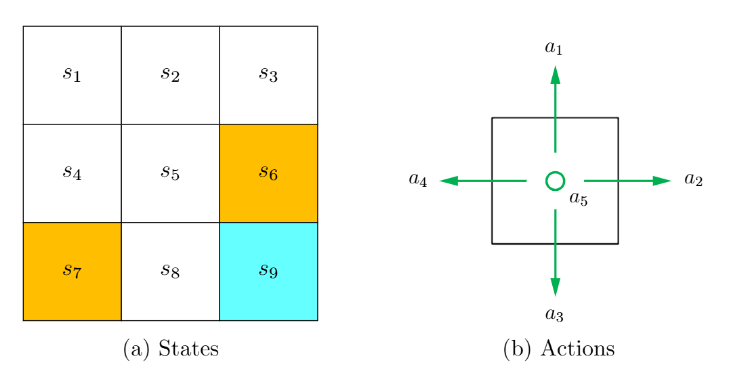
状态和动作

状态（state）用来描述智能体与环境的相对状况，网格世界中的9个单元格对应9的状态，用 $s_{1},s_{2},s_{3},\cdot \cdot \cdot ,s_{9}$ 表示。所有状态的集合称为状态空间（state space）用 $S=\left \{s _{1} ,s_{2},\cdot \cdot \cdot,s_{9} \right \}$ 表示，如图（a）。

动作（action）用来表示智能体在每一个状态的可选动作，即向上、向右、向下、向左，用 $a_{1},a_{2},a_{3},\cdot \cdot \cdot ,a_{5}$ 表示。这些动作的集合称为动作空间（stata space）用 $A=\left \{a _{1} ,a_{2},\cdot \cdot \cdot,a_{5} \right \}$ 表示，如图（b）。

你可能会问：比如智能体在 $s_{1}$ 状态时，是不是可以设置 $s_{1}$ 状态的动作空间为 $A\left ( s_{1} \right )=\left \{a _{2} ,a_{3},a_{5} \right \}$ 呢？答案是可以的，不过本书中只考虑最一般的情况，即 $A\left ( s \right )=\left \{a _{1} ,a_{2},\cdot \cdot \cdot,a_{5} \right \}$ 。我们并不人为避开其中不合理的动作，而是要通过算法学习来判断。

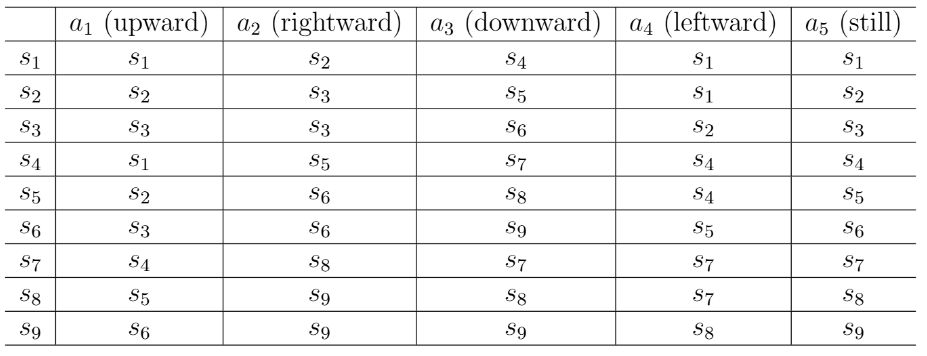
状态转移

智能体可能从一个状态转移到另一个状态，这样的过程称为状态转移（state transition），比如智能体在状态 $s_{1}$ 并且执行动作 $a_{2}$ （即向右移动），那么智能体会在下个时刻移动到状态 $s_{2}$ ，这样的过程表示为

$s_{1}\overset{a_{2}}{\rightarrow}s_{2}$ .

特别的，基于上面的规则，智能体“撞墙”和穿过禁区是允许的，即 $s_{1}\overset{a_{1}}{\rightarrow}s_{1}$ ， $s_{5}\overset{a_{2}}{\rightarrow}s_{5}$ 成立。

状态转移的过程可以用表格来描述，每行对应一个状态，每列对应一个动作，每个单元格给出了智能体会转移到的下一个状态。

虽然直观，但是表格只能描述确定性的（deterministic）状态转移过程。当然，状态转移也可以是随机的（stochastic），此时需要条件概率来描述。数学上，在确定情况下用条件概率描述刚才的例子：

$p\left ( s_{1}\mid s_{1},a_{2} \right )= 0$ ,

$p\left ( s_{2}\mid s_{1},a_{2} \right )= 1$ ,

$p\left ( s_{3}\mid s_{1},a_{2} \right )= 0$ ,

$\vdots$

$p\left ( s_{9}\mid s_{1},a_{2} \right )= 0$ ,

该条件概率告诉我们：当在状态 $s_{1}$ 采取动作 $a_{2}$ 时，智能体转移到状态 $s_{2}$ 的概率是1，而其他任意状态的概率为0。

随机的情况：假如网格世界中有随机的阵风吹过，这时候在状态 $s_{1}$ 采取动作 $a_{2}$ 时，智能体很有可能被阵风吹到 $s_{5}$ 而不是 $s_{2}$ 。在这种情况下，则有 $p\left ( s_{5}\mid s_{1},a_{2} \right )> 0$ ，即下一个状态具有不确定性。不过简单起见，在本书网格世界的例子中，我们只考虑确定性的状态转移过程。

策略

策略（policy）会告诉智能体在每一个状态应该采取什么样的动作。策略可以通过箭头来描述，若智能体执行某一策略，那么它会从初始状态生成一条轨迹，如下图。

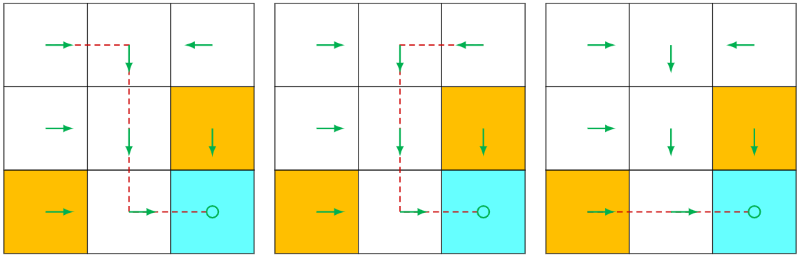
$\pi \left ( a\mid s \right )$ 表示在状态 $s$ 采取动作 $a$ 的概率（注意这里的 $\pi$ 不是圆周率！）

结合上面状态转移的概念，我们可以得出：若确定的策略生成的轨迹，其中一段是 $s_{1}\overset{a_{2}}{\rightarrow}s_{2}$ ，则 $\pi \left ( a_{2}\mid s_{1} \right )=1$ ，在状态 $s_{1}$ 采取其他动作的概率均为0。

策略也可能是随机性的。如下图，在状态 $s_{1}$ ，智能体有0.5的概率采取向右的动作，有0.5的概念采取向下的动作。此时则有

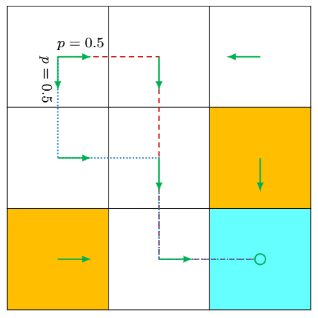
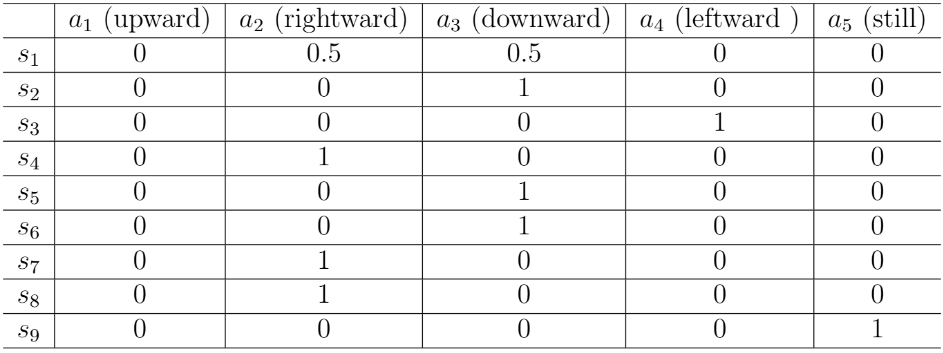
$\pi \left ( a_{2}\mid s_{1} \right )=0.5$ ， $\pi \left ( a_{3}\mid s_{1} \right )=0.5$ .

当然策略也可以用表格来描述。这样的描述方法被称为表格表示法（tabular representation）。

奖励

奖励（reward）的设定简单来说就是我们对智能体执行的动作进行评分。当智能体执行一个的动作后会获得奖励 $r$ 。 $r$ 是一个实数，它是状态 $s$ 和动作 $a$ 的函数，即 $r\left ( s,a \right )$ 。奖励 $r$ 为正代表我们鼓励该动作，奖励为负则代表我们不鼓励该动作。

在本章网格世界的例子中，我们设置无效（撞墙）和违规（穿过禁区）动作获得奖励 $r$ 为负，到达目的地获得奖励 $r$ 为正，其余动作获得奖励 $r$ 为0，即

$r_{boundary}=-1$ ,

$r_{forbidden}=-1$ ,

$r_{target}=+1$ ,

$r_{other}=0$ ,

同样的，奖励的过程可以用表格和条件概率描述。

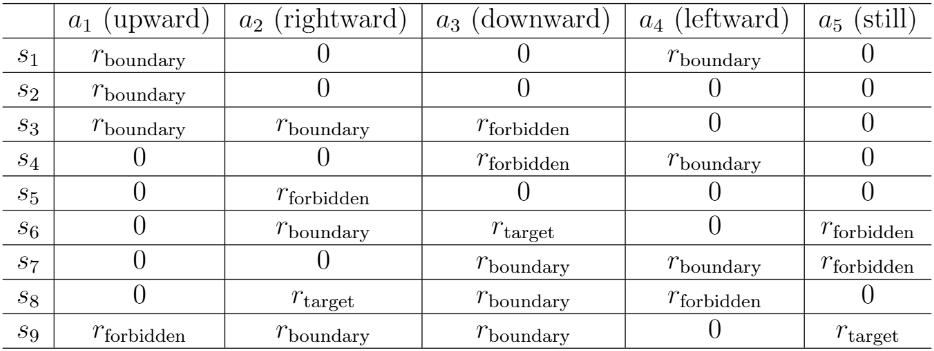
注意：这些奖励只是即时奖励（immediate reward），即在采取一个动作后可以立刻获得的奖励。一个好的策略必须考虑更长远的总奖励（total reward）。具有最大的即时奖励的动作不一定能带来最大的总奖励。

表格只能描述确定性的奖励过程，然而条件概率可以描述更加一般化的奖励过程： $p\left ( r \mid s,a \right )$ 表示在状态 $s$ 采取动作 $a$ 得到奖励 $r$ 的概率。在前面的例子，对状态 $s_{1}$ ，有

$p(r=-1 \mid s_{1},a_{1})=1$ ， $p(r\neq -1 \mid s_{1},a_{1})=0$ ,

如果奖励过程是随机的，例如 $p(r=-1 \mid s_{1},a_{1})=0.5$ ， $p(r\neq -2 \mid s_{1},a_{1})=0.5$ 表示各有0.5的概率获得-1或者-2的奖励。本书的网格世界的例子都只考虑确定的奖励过程。

轨迹、回报、回合

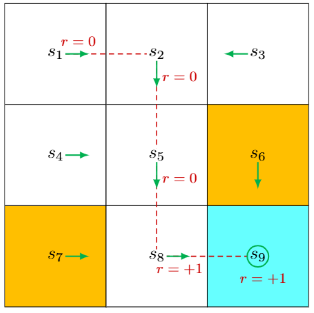
轨迹（trajectory）指的是一个“状态-动作-奖励”的链条。如图()所示的策略，智能体从 $s_{1}$ 出发会得到如下轨迹：

$s_{1}\xrightarrow[r=0]{a_{2}}s_{2}\xrightarrow[r=0]{a_{3}}s_{5}\xrightarrow[r=0]{a_{3}}s_{8}\xrightarrow[r=1]{a_{2}}s_{9}$ .

回报(return)是指沿着一条轨迹智能体获得一系列的即时奖励之和，可以用于评价一个策略的好坏。回报也可以称为总奖励（total reward）或累积奖励（cumulative reward）。上述轨迹对应回报为

$return = 0+ 0 + 0 + 1 = 1$ .

回报由即时奖励（immediate reward）和未来奖励（future reward）组成。即时奖励前面说过不再赘述。未来奖励是指智能体离开初始状态后获得的奖励之和。上述轨迹对应的即时奖励是0，未来奖励是1，总奖励则是1.

当智能体到达目标状态 $s_{9}$ 之后，它也许会持续执行策略，进而持续获得奖励。若智能体在 $s_{9}$ 采取动作 $a_{5}$ （保持不动），此时会继续获得奖励 $r_{target}=+1$ ，也就是说如果它学会了“刷分”，计算回报得到的是

$return = 0+ 0 + 0 + 1 + 1 + 1 +\cdots = \infty$ ,

由于计算出的回报会发散到无穷，所以我们需要引入折扣回报（discounted return）的概念。令 $\gamma \in \left ( 0,1 \right )$ 为折扣因子（discount rate），折扣回报是指折扣奖励的总和，即为不同时刻得到的奖励添加相应的折扣再求和：

$discounted\; return = 0+ \gamma 0 + \gamma ^{2}0 + \gamma ^{3}1 + \gamma ^{4}1 + \gamma ^{5}1 +\cdots$

由此以来折扣回报就变成了一个等比数列：

$discounted\; return =\gamma ^{3} \left ( 1+\gamma +\gamma ^{2}+\cdots \right )= \gamma ^{3}\frac{1}{1-\gamma }$ .

我的个人理解：折扣回报就是当智能体离开初始状态之后每次的奖励都乘上 $\gamma$ 的 $t$ 时刻次方，然后将其累加起来计算出的回报。

回合（episode）是指智能体在终止状态（terminal state）停止的过程。需要与神经网络训练过程程中的回合（epoch）加以区分。

任务分为两类：

如果一个任务最多有有限步，那么这样的任务称为回合制任务（episodic tast）。
如果智能体与环境的交互永不停止，这种任务被称为持续性任务（continuing task）。

为了在数学上可以不加区分的对待这两种任务，我们可以把回合制任务转换为持续性任务。本书中，我们将目标状态视为一个普通状态，其动作空间为 $A=\left \{ a_{1}, a_{2},\cdots , a_{5} \right \}$ 。由于智能体到达这个状态之后仍然允许离开这个状态，因此这是一种更加一般化的情况，我们需要让智能体学习到在到达这状态之后能够保持原地不动。值得注意的是，我们需要使用折扣因子，来避免回报趋于无穷。

掌握上述概念后，理解马尔可夫决策过程（Markov decision process，MDP）就变得容易多了。

马尔可夫决策过程

马尔可夫决策过程（Markov decision process，MDP）是描述随机动态是系统的一般框架。整个强化学习需要基于这个框架。关键要素包括集合、模型、策略还有马尔可夫性质。

我个人总结为三个集合+两个模型+一个策略+马尔可夫性质，有了前面的铺垫理解起来就不那么难了。

三个集合：

状态空间：所有状态的集合，记为 $S$ 。
动作空间：与每个状态 $s\in S$ 相关联的所有动作的集合，记为 $A\left ( s \right )$ 。
奖励集合：与 $\left ( s,a \right )$ 相关联的所有奖励的集合，记为 $R\left ( s, a \right )$ 。

两个模型

状态转移概率：在状态 $s$ 采取动作 $a$ 时，智能体转移到 ${s}'$ 的概率为 $p\left ( {s}' \mid s,a\right )$ 。对于任意 $\left ( s,a \right )$ ，都有 $\sum_{{s}'\in S}^{}p\left ( {s}' \mid s,a\right )=1$ 。
奖励概率：在状态 $s$ 采取动作 $a$ 时，智能体获得奖励 $r$ 的概率是 $p\left ( r \mid s,a\right )$ 。对于任意 $\left ( s,a \right )$ ，都有 $\sum_{r\in R\left ( s, a \right )}^{}p\left ( r \mid s,a\right )=1$ 成立。

一个策略

在状态 $s$ ，智能体采取动作 $a$ 的概率是 $\pi \left ( a\mid s \right )$ 。对应任意 $s\in S$ ，都有 $\sum_{a\in A\left ( s \right )}^{}\pi \left ( a\mid s \right )=1$ 。

马尔可夫性质

马尔可夫性质（Markov property）是指随机过程中的无记忆性质，它数学上表示为

$p\left ( s_{t+1} \mid s_{t},a_{t},s_{t-1},a_{t-1},\cdots s_{0},a_{0} \right )=p\left ( s_{t+1} \mid s_{t},a_{t} \right )$ ,

$p\left ( r_{t+1} \mid s_{t},a_{t},s_{t-1},a_{t-1},\cdots s_{0},a_{0} \right )=p\left ( r_{t+1} \mid s_{t},a_{t} \right )$ ,

其中 $t$ 表示当前时刻， $t+1$ 表示下一时刻。上述式子表示下一个状态和奖励仅依赖于当前时刻的状态和动作，而与之前时刻的状态和动作无关。

一旦在马尔可夫决策过程中的决策确定下来，马尔可夫决策过程就退化成一个马尔可夫过程（Markov process，MP）。本书主要考虑有限的马尔可夫决策过程，即状态和动作的数量都是有限的。下图中的网格世界策略已经给定，此时整个系统可以被抽象为一个马尔可夫过程。

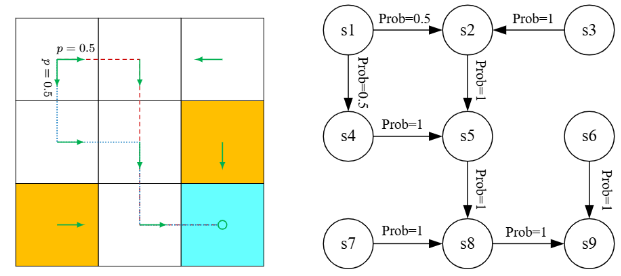
总结

我们在学习了状态、动作、奖励、回报、策略等基本概念，后面再理解马尔可夫决策过程就不是那么困难了，再次感谢这本书的作者赵世钰老师。后面我们将继续学习状态值（state value）以及贝尔曼方程（Bellman equation），之后我会把我学习RL的过程写进一个专栏，大家持续的关注我吧！

制作不易，对您有帮助的话就点赞收藏支持一下，感谢感谢~