VTK实现三维地质建模

原创已于 2022-05-12 11:00:17 修改 · 3.8k 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#vtk #可视化

于 2021-05-25 23:09:51 首次发布

VTK三维可视化开发专栏收录该内容

5 篇文章

订阅专栏

前言

本文不适合0基础的VTK开发者，需要提前了解VTK可视化管线和渲染引擎的概念和流程，建议先阅读《VTK图形图像开发进阶》这本书稍微了解一下，并且根据里面的学习案例对VTK有一些了解。 VTK真的不是装好就能上手用的，相比之下OpenCV这种图像处理库真的好用。
本文主要参考文献【1】基于 VTK 和 QT 的层状地质体三维建模及可视化研究—姜弢、陈振振、徐学纯
【2】基于VTK技术的三维地层可视化研究_刘玉芳

目前,地质体三维数据模型总体上可分为线模型、表面模型、实体模型、面向对象的三维数据模型及混合数据模型五大类型。线模型的优点是集合关系明确,缺点是对于实体间关系表达及实现交、并等叠加操作较困难。表面模型的优点是便于边界约束、显示和数据更新,缺点是空间分析难以进行。实体模型的优点是便于空间操作和分析,缺点是占用空间较大,计算速度也较慢。面向对象的三维数据模型和混合数据模型分别综合了线、表面、实体模型的优缺点,但实现算法复杂。[1]基于 VTK 和 QT 的层状地质体三维建模及可视化研究—姜弢、陈振振、徐学纯
本文采用表面模型和体模型混合建模的方式进行地质体三维建模。采用面模型和体模型混合建模的原因是只有面模型不能够准确地描述层状地质体内部的信息，但是面模型可以对层状地质体的边界进行约束。其次，对每个地层顶面和底面用体模型进行填充，常用的体模型有四面体、三棱柱和六面体，其中四面体模型可以构造非常复杂的地层模型，但是由于四面体数据拓扑结构复杂，数据冗余量大，运算负荷大，对计算机的要求较高，故使用广义三棱柱进行填充。[1]基于 VTK 和 QT 的层状地质体三维建模及可视化研究—姜弢、陈振振、徐学纯

一、构建不规则三角网（TIN）

三棱柱构模原理是由上下两个不平行的两个TIN三角形面和三个竖直侧面四边形面所组成的空间单元。【2】
一般使用Delaunay三角剖分算法对空间中不规则的三维散点集合进行三角剖分。
VTK的vtkDelaunay2D类实现了二维三角剖分。该类的输入数据为一个vtkPointSet或其子类表示的三维空间点集，其输出是一个三角网格vtkPolyData数据。虽然输入的是三维数据，但是算法仅使用XY平面数据进行平面三角剖分，而忽略Z轴的数据。当然，也可以为vtkDelaunay2D设置投影变换从而在新的投影平面上进行三角剖分。

1.1 构建模拟的地层数据

由于手上没有实际测量得到的地层表面散点数据，故只能自己构建一些点来建立地层模型。
这里构建的散点都是规则的点，即确定地层表面在X和Y方向上的点数Nx,Ny，形成规则格网，即等间隔矩形网格，通过格网线之间的间隔来描述或定义，同一个坐标轴上格网线间隔值相同，不同轴向上的格网线间隔值可以不同。通过定义开始点及每个坐标方向上的增量来显示指定坐标。【2】。对于实际测量得到的地层表面数据，可以对其进行离散点格网化，就是对每一个岩层层面离散点进行格网剖分，每个数据点记录了剖分后格网点的平面坐标及高程，共三列，依次记录坐标X,坐标Y，高程Z。
使用插值算法将离散点，如反距离加权插值算法、克里金插值算、最小曲率方法等，具体的我也还没开始研究，因为现在手上没有实际的测量数据。

构建一层地层，包括上表面和下表面：

	vtkSmartPointer<vtkPoints> points=vtkSmartPointer<vtkPoints>::New();
	unsigned int GridSize_X = 10,GridSize_Y=10;//10*10个等间距的点，也可以使X和Y方向上的点间隔不同
	unsigned int id=0,num=0;
	double z=0;
	//先生成上表面点数据，在生成下表面点数据
	for(int i =0;i<2;i++)
	{
		std::cout<<"level ： "<<i<<endl;
		for (unsigned int x = 0; x < GridSize_X; x++)
		{
			for (unsigned int y = 0; y < GridSize_Y; y++)
			{
				z=i*(-5) + vtkMath::Random(0,1);
				id=points->InsertNextPoint(x, y, z);
			}
		}
		std::cout<<std::endl;
	}
	std::cout<<points->GetNumberOfPoints()<<std::endl;

把两个界面的数据用vtkPoints对象points存放。注意：顶面和底面数据点的x 和y值相同，不同的只有z值，通过Z值可以区分不同地层之间的距离以及是否存在尖灭。

1.2 Delaunay三角剖分

使用VTK的vtkDelaunay2D类实现了对地层表面散点数据二维三角网剖分，为什么使用二维？因为这里的顶面和底面数据点的x和y相同（其实就算不同也可以不用考虑Z，不过要分开两个面进行三角剖分），不同的是Z值，我们要的结果是把这些点数据相互连接生成三角形拓扑，而我们使用三角形作为三棱柱的两个三角面，故生成三角形实际与Z值高程无关，只需要使用x和y值就行，最后再连接起该点形成三角形.
。由于使用的是三棱柱作为体元，使用顶面中生成的三角形作为三棱柱体元的上三角形，对应底面中生成的三角形作为三棱柱体元的下三角形，把这两个三角形拓扑关系所对应的散点数据进行连接，即可构成一个三棱柱模型。
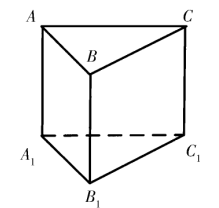
在这里插入图片描述
对于同一地层的顶面和底面数据点要分开进行Delaunay三角剖分，这里是在上下两个面的点数据X和Y相同的情况下，如果不分开进行三角剖分的话，可能只会对顶面或底面进行三角剖分；倘若是上下两个面的点数据X和Y不同的情况，那就更容易出问题了，因为Dealunay2D只对XY平面进行三角剖分，即算法此时可能会把上下两个面的点当成是一个面的，然后进行三角剖分，则上下两个面的点就连接成三角形了。

	//分离地层的顶部和底部地层表面数据点，本质是拷贝数据点到ceil和bottom
	vtkSmartPointer<vtkPoints> ceil = vtkSmartPointer<vtkPoints>::New();
	for (int i = 0; i < GridSize_X*GridSize_Y; ++i)
	{
		auto point = points->GetPoint(i);
		ceil->InsertNextPoint(point);
		cout<<"ceil	point = "<<point[0]<<","<<point[1]<<","<<point[2]<<endl;
	}

	vtkSmartPointer<vtkPoints> bottom = vtkSmartPointer<vtkPoints>::New();
	for (int i = GridSize_X*GridSize_Y; i < points->GetNumberOfPoints(); ++i)
	{
		auto point = points->GetPoint(i);
		bottom->InsertNextPoint(point);
		cout<<"bottom	point = "<<point[0]<<","<<point[1]<<","<<point[2]<<endl;
	}
	// Add the grid points to a polydata object
	vtkSmartPointer<vtkPolyData> polydata=vtkSmartPointer<vtkPolyData>::New();
	polydata->SetPoints(points);
	vtkSmartPointer<vtkPolyData> ceil_polydata =
		vtkSmartPointer<vtkPolyData>::New();
	ceil_polydata->SetPoints(ceil);
	vtkSmartPointer<vtkPolyData> bottom_polydata =
		vtkSmartPointer<vtkPolyData>::New();
	bottom_polydata->SetPoints(bottom);

	// Triangulate the grid points
	vtkSmartPointer<vtkDelaunay2D> ceil_delaunay =
		vtkSmartPointer<vtkDelaunay2D>::New();
	ceil_delaunay->SetInputData(ceil_polydata);
	ceil_delaunay->Update();

	vtkSmartPointer<vtkDelaunay2D> bottom_delaunay =
		vtkSmartPointer<vtkDelaunay2D>::New();
	bottom_delaunay->SetInputData(bottom_polydata);
	bottom_delaunay->Update();

	//上下三角网combine two poly data
	vtkSmartPointer<vtkAppendPolyData> appendfilter = vtkSmartPointer<vtkAppendPolyData>::New();
	appendfilter->AddInputConnection(ceil_delaunay->GetOutputPort());
	appendfilter->AddInputConnection(bottom_delaunay->GetOutputPort());

	vtkSmartPointer<vtkPolyDataMapper> meshMapper =
		vtkSmartPointer<vtkPolyDataMapper>::New();
	meshMapper->SetInputConnection(appendfilter->GetOutputPort());

此时把meshMapper送入渲染引擎，便可以看到上下两个面三角剖分后的结果。
在这里插入图片描述

二、构建地质三棱柱体模型

1.生成三棱柱体元

目前按我查到的资料来看，构建三棱柱都需要用到插入点数据到vtkPoints对象时返回的ID值，id=points->InsertNextPoint(x, y, z); 返回该点在points中的索引。但是我比较迷惑，就是例如下面这种情况：

    unsigned int GridSize = 10;
	for (unsigned int x = 0; x < GridSize; x++)
	{
		for (unsigned int y = 0; y < GridSize; y++)
		{
			points->InsertNextPoint(x, y, vtkMath::Random(0,1));//返回该point的ID
		}
	}
	vtkSmartPointer<vtkWedge> wedge =
        vtkSmartPointer<vtkWedge>::New();

    //SetID的顺序必须是三棱柱的上三角形的三个点ID和下三角形的三个点ID
    wedge->GetPointIds()->SetId(0, 0);//第一个参数是三棱柱的6个点序号，第二个参数是vtkPoints对象中的点ID，就是插入是返回的那个
    wedge->GetPointIds()->SetId(1, 2);
    wedge->GetPointIds()->SetId(2, 20);
    wedge->GetPointIds()->SetId(3, 1);
    wedge->GetPointIds()->SetId(4, 3);
    wedge->GetPointIds()->SetId(5, 21);

注意：这里我比较迷惑的是为什么SetId()里的第二个参数就只用一个数字来表示ID就可以了，那系统是怎么确定这个数字代表的是哪个vtkPoints对象的点ID？经过我的实验发现，这个数字代表的ID貌似指定的是距离SetId()最近的在它之前插入vtkPoints对象的点的ID,那就类似与就近原则？那假设当前代码中有多个vtkPoints对象，我想利用前面几个vtkPoints对象的ID点来构建三棱柱怎么办？这个我暂时还没搞到答案，群里问了半天也没人回答，有大佬知道的可以评论一下，VTK的点ID管理，网上是真的找不到啥资料，这个问题折腾了我好久了。
而且由于这个问题没有得到解决，使用Delaunay2D生成的三角形我也没有办法知道每个三角形对应的点ID是多少，所以我构建三棱柱用的点ID就是vtkPoints对象中点插入后返回的ID。

这里我构建三棱柱就是按照这种“就近原则”，把构建三棱柱的代码紧跟在vtkPoints对象的点插入之后。ID是按点插入的顺序来确定的，构建三棱柱时需要注意，构造三棱柱的6个点的id都是我推理计算出来的。

/**
 * MakeWedge必须紧跟在地层表面数据生成或读入之后，然后利用其ID来构建三棱柱，同时对地层表面数据读入或生成的顺序有要求，先Y后X
 * 这个函数构建的是三棱柱集合
 * */
vtkSmartPointer<vtkUnstructuredGrid> MakeWedge(vtkSmartPointer<vtkPoints> points,unsigned int GridSize_X,unsigned int GridSize_Y)
{
	vtkSmartPointer<vtkUnstructuredGrid> ug =
        vtkSmartPointer<vtkUnstructuredGrid>::New();
    ug->SetPoints(points);

	vtkIdType p=0;//设置一个ID编号
	//每列GridSizeY-1个矩形格子，每行GridSizeX-1个矩形格子
	for(int i=1;i<GridSize_X;i++)//从矩形格子开始统计，一个矩形格子可以划分为两个三角形，
	{
		for(int j=1;j<GridSize_Y;j++)
		{
			//先构造矩形格网的左下三棱柱
			//SetID的顺序必须是三棱柱的上三角形的三个点ID和下三角形的三个点ID
			vtkSmartPointer<vtkWedge> wedge1 =
        		vtkSmartPointer<vtkWedge>::New();
			wedge1->GetPointIds()->SetId(0, p);
			wedge1->GetPointIds()->SetId(1, p+1);
			wedge1->GetPointIds()->SetId(2, p+GridSize_Y);
			//下三角形ID
			wedge1->GetPointIds()->SetId(3, GridSize_X*GridSize_Y+p);
			wedge1->GetPointIds()->SetId(4, GridSize_X*GridSize_Y+p+1);
			wedge1->GetPointIds()->SetId(5, GridSize_X*GridSize_Y+p+GridSize_Y);

			//添加三棱柱
			//if(p==4)
			ug->InsertNextCell(wedge1->GetCellType(), wedge1->GetPointIds());
			//先构造矩形格网的左下三棱柱
			vtkSmartPointer<vtkWedge> wedge2 =
        		vtkSmartPointer<vtkWedge>::New();
			wedge2->GetPointIds()->SetId(0, p+1);
			wedge2->GetPointIds()->SetId(1, p+GridSize_Y+1);
			wedge2->GetPointIds()->SetId(2, p+GridSize_Y);
			//下三角形ID
			wedge2->GetPointIds()->SetId(3, GridSize_X*GridSize_Y+p+1);
			wedge2->GetPointIds()->SetId(4, GridSize_X*GridSize_Y+p+GridSize_Y+1);
			wedge2->GetPointIds()->SetId(5, GridSize_X*GridSize_Y+p+GridSize_Y);
			//if(p==-3)
			ug->InsertNextCell(wedge2->GetCellType(), wedge2->GetPointIds());
			p++;
			if(j==GridSize_Y-1)//点ID到达矩形网格最上边界之后，直接跳转到下一个ID
				p++;
		}
	}
    return ug;
}

int main(int, char *[])
{
	vtkSmartPointer<vtkPoints> points=vtkSmartPointer<vtkPoints>::New();
	unsigned int GridSize_X = 10,GridSize_Y=10;
	unsigned int id=0,num=0;
	double z=0;
	//先生成上表面点数据，在生成下表面点数据
	for(int i =0;i<LEVEL;i++)
	{
		std::cout<<"level "<<i<<endl;
		for (unsigned int x = 0; x < GridSize_X; x++)
		{
			for (unsigned int y = 0; y < GridSize_Y; y++)
			{
				z=i*(-5) + vtkMath::Random(0,1);
				//z=(i-0.5)*(GridSize_X-x);
				id=points->InsertNextPoint(x, y, z);
			}
		}
		std::cout<<std::endl;
	}
	std::cout<<points->GetNumberOfPoints()<<std::endl;
	//构建三棱柱集合
	vtkSmartPointer<vtkUnstructuredGrid> wedgeArray=MakeWedge(points,GridSize_X,GridSize_Y);

到这里这一层地层的不规则三角形（TIN）面和三棱柱体元就建立好了。想要在窗口中显示出来，还需要配置VTK的可视化管线和渲染引擎。

	vtkSmartPointer<vtkUnstructuredGrid> wedgeArray=MakeWedge(points,GridSize_X,GridSize_Y);
	// Visualize
	vtkSmartPointer<vtkNamedColors> WedgeColor =
		vtkSmartPointer<vtkNamedColors>::New();
	//三棱柱映射
    vtkSmartPointer<vtkDataSetMapper> wedgeMapper = vtkSmartPointer<vtkDataSetMapper>::New();
    wedgeMapper->SetInputData(wedgeArray);
	vtkSmartPointer<vtkActor> wedgeActor=vtkSmartPointer<vtkActor>::New();
    wedgeActor->SetMapper(wedgeMapper);
	wedgeActor->GetProperty()->SetColor(WedgeColor->GetColor3d("Banana").GetData());
	wedgeActor->GetProperty()->EdgeVisibilityOn();//显示三角形的边

	vtkSmartPointer<vtkRenderer> renderer =
		vtkSmartPointer<vtkRenderer>::New();
	renderer->AddActor(wedgeActor);//显示三棱柱体元
	renderer->SetBackground(colors->GetColor3d("Mint").GetData());
	vtkSmartPointer<vtkRenderWindow> renderWindow =
		vtkSmartPointer<vtkRenderWindow>::New();
	renderWindow->AddRenderer(renderer);
	vtkSmartPointer<vtkRenderWindowInteractor> renderWindowInteractor =
		vtkSmartPointer<vtkRenderWindowInteractor>::New();
	renderWindowInteractor->SetRenderWindow(renderWindow);
	renderWindow->Render();
	renderWindowInteractor->Start();

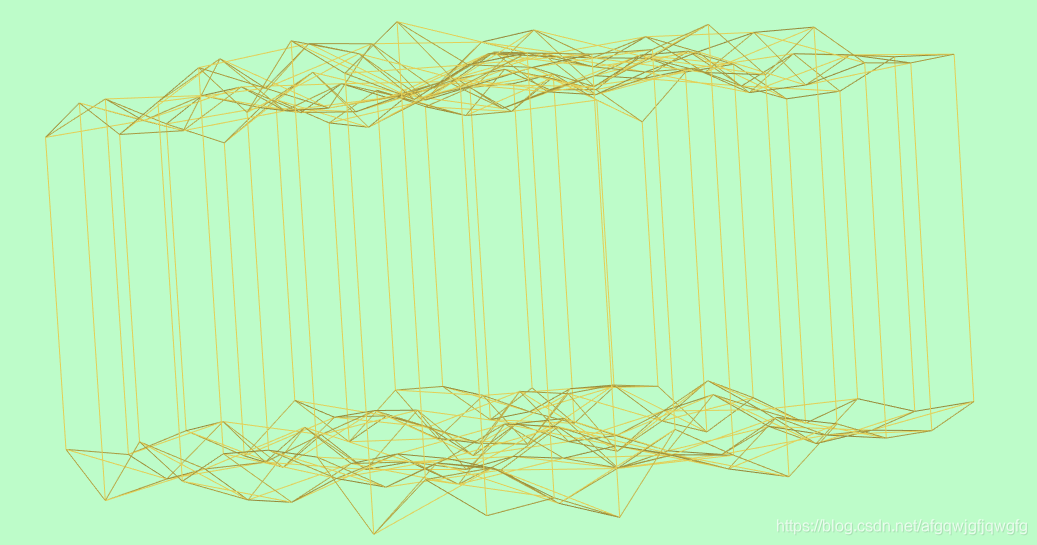
在这里插入图片描述

总结

我是第一次使用VTK建模，完成这一层地层建模就花了我差不多两个多星期，虽然完成了，但是还是有很多疑惑还是没有解决，在查找问题的过程中我也发现，优快云上VTK对应的文章挺多的，但是都不怎么系统，遇到一些问题，想问问别人却几年都没有回应，VTK贴吧更是冷清，在QQ上找了个vtk开发群700多个人，在线的不到100，会帮忙回答问题的更是少之又少。这一点和OSG那边真的形成鲜明对比，OSG那边好像是有个专门的使用OSG开发的国内公司在管理，群里面也是他们在帮忙解答一些问题，而且群里人很多，问一个问题基本马上就有回复，还有出一些中文教程。唉，要是VTK也有这样的组织就好了。