#LeetCode刷题——121.买卖股票的最佳时机-优快云博客

本文链接：https://blog.youkuaiyun.com/aetawt/article/details/122367662

本文解析了如何利用动态规划解决股票交易中的最大利润问题，通过两种方法对比，介绍了暴力法和动态规划算法，展示了从计算当天买入最低价到获取最大利润的过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

难度：easy

1、题目介绍

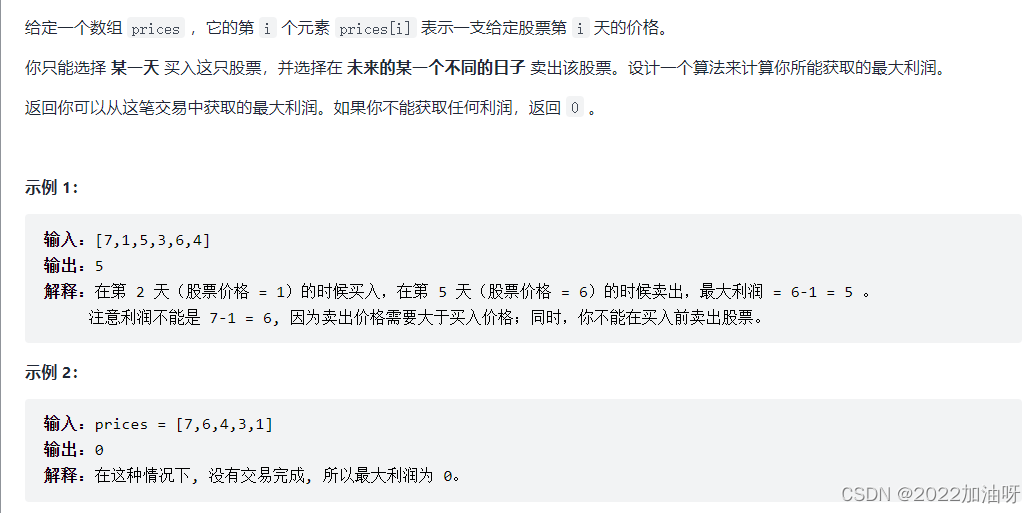
2、思路分析【与求最大子序列的和类似】

第一种方法：暴力法

1、假设最大利润maxProfit = 0 ，使用俩个指针 i 和 j ，不断的将 j 所指向的元素减去 i 所指向的元素，结果如果比maxProfit的值大，就将maxProfit指向这个比较大的值，最终返回maxProfit

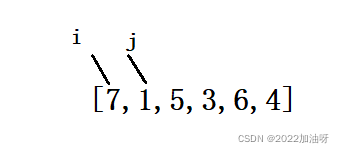
i 指向 7 时： 1-7 < maxProfit , 将 j 后移 5- 7 < maxProfit , 再将 j 后移 .......

i 指向 1 时：5 - 1 > maxProfit , maxProfit = 4 .......

代码：

 //第一种方法：暴力法【与俩数之和类似】
    public static int maxProfit(int[] prices) {
        int maxProfit = 0;//保存最大利润,假设是0
        for (int i = 0; i < prices.length; i++) {
            for (int j = i + 1; j < prices.length; j++) {
                int profit = prices[j] - prices[i];
                if (profit > maxProfit) {
                    maxProfit = profit;
                }
            }
        }
        return maxProfit;
    }

第二种方法：动态规划

           求当天的买入价格和前一个的买入价格的最小值，获得动态方程：
                dp[i] = Math.min(dp[i-1],prices[i]).
       求利润的最大值：maxProfit = Math.max(maxProfit, prices[i] - dp[i]);

代码：

  //第二种方法：动态规划
    public static int maxProfit1(int[] prices) {
        //dp[i]保存第 i 天的买入价格最低点。因为要求最大利润，所以要求买入的最小值，卖出的最大值
        int[] dp = new int[prices.length];
        dp[0] = prices[0];
        int maxProfit = 0;
        for (int i = 1; i < prices.length; i++) {
            //当前买入价格与前一买入个价格作比较，求最小值
            dp[i] = Math.min(dp[i - 1], prices[i]);
            maxProfit = Math.max(maxProfit, prices[i] - dp[i]);
        }
        return maxProfit;
    }