利用迭代回溯解决迷宫问题

华为机考例题:

定义一个二维数组N*M（其中2<=N<=10;2<=M<=10），如5 × 5数组下所示： 
int maze[5][5] = {
        0, 1, 0, 0, 0,
        0, 1, 0, 1, 0,
        0, 0, 0, 0, 0,
        0, 1, 1, 1, 0,
        0, 0, 0, 1, 0,
};
它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。入口点为[0,0],既第一空格是可以走的路。

Input

一个N × M的二维数组，表示一个迷宫。数据保证有唯一解,不考虑有多解的情况，即迷宫只有一条通道。

Output

左上角到右下角的最短路径，格式如样例所示。

Sample Input

0 1 0 0 0

0 1 0 1 0

0 0 0 0 0

0 1 1 1 0

0 0 0 1 0

Sample Output

(0, 0)

(1, 0)

(2, 0)

(2, 1)

(2, 2)

(2, 3)

(2, 4)

(3, 4)

(4, 4)

看了例题，开始动手，想想怎么解决问题。

1、只有0可以走，1不可以走，所以在接收迷宫时，只保存值为0的位置，即当（x，y） =  0 时保存x,y到固定数组，按x的正方向和y的正方向放置。

如下图代码二维数组pos存储当值为0时x,y的位置，i的值为所有通点的总数。

int main()
{
    int len1 = 0, len2 = 0, n = 0;
	int pos[100][3] = { {0} };

	int pos_x[100] = { 0 };
	int pos_y[100] = { 0 };
	int pos_i = 0;
	while (scanf("%d%d", &len1, &len2) != EOF)
	{
		int i = 0;
		for (int x = 0; x < len1; x++)
			for (int y = 0; y < len2; y++)
			{
				scanf("%d", &n);
				if (n == 0)
				{
					pos[i][0] = x;
					pos[i++][1] = y;
				}
			}
    }
}

2、一个点可以上下左右四个方向运动，但是要求最短路径，肯定是优先向下或者向右走

这里设置优先级-下右上左。

情况一：

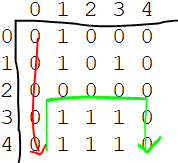
依据下右上左的优先级，设点A从（0，0）出发，第一次的路径为(0,0)->(1,0)->(2,0)->(3,0)->(4,0)，当走到（4，0），发现没有路了，只能回头一步到（3，0），还是没有路，再回头一步到（2，0），发现（2，0）有一条向右的路可以走，沿着这条路走，可以最后直达（4，4）。

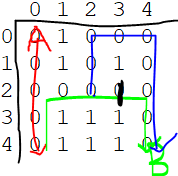
情况二：

当（2，3）从通点变成墙壁。

依据下右上左的优先级，设点A从（0，0）出发，第一次的路径为(0,0)->(1,0)->(2,0)->(3,0)->(4,0)，当走到（4，0），发现没有路了，只能回头一步到（3，0），还是没有路，再回头一步到（2，0），发现（2，0）有一条向右的路可以走，沿着这条路走，

发现向右和向下都堵死了，只能向上走了，新路径变成蓝色的样子。

代码：

解析：整形数组pos_x和pos_y存放可以走的通路，从起点（0，0）到终点（4，4）。

每到一个新点，从整形二维数组pos中从大到小查找相邻的点，若有，则放入整形数组pos_x,pos_y，并将该点标记为走过，即pos[x][2]++; 若没有，则整形数组pos_x,pos_y回退一个，重新查找。

#include "stdio.h"

int main()
{
	int len_x = 0, len_y = 0;
	while (scanf("%d%d", &len_x, &len_y) != EOF)
	{
		int i = 0, pos_i = 0,n = 0;
		int pos_x[100] = { 0 };
		int pos_y[100] = { 0 };
		int pos[100][3] = { {0} };
        
		for (int x = 0; x < len_x; x++)
			for (int y = 0; y < len_y; y++)
			{
				scanf("%d", &n);
				if (n == 0)
				{
					pos[i][0] = x;
					pos[i++][1] = y;
				}
			}
		while (1)
		{
			if ((pos_x[pos_i] == len_x-1) && (pos_y[pos_i] == len_y-1))
				break;
			int flag = 0;
			int k = i;
			for (; k > 0; k--)
			{
				int px = pos[k-1][0] - pos_x[pos_i];
				int py = pos[k-1][1] - pos_y[pos_i];
				if ((px == 0 && py == 1) || (px == 1 && py == 0) || (px == 0 && py == -1) || (px == -1 && py == 0))
				{
					if (pos[k - 1][2] == 0)
					{

						pos_x[++pos_i] = pos[k - 1][0];
						pos_y[pos_i] = pos[k - 1][1];
						pos[k - 1][2]++;
						flag = 1;
						break;
					}
				}
			}
			
			if (flag == 0)
			{
				// no found
				pos_x[pos_i] = 0;
				pos_y[pos_i] = 0;
				
				if (pos_i > 0) 
				{
					pos_i--;
				}
				else
				{
					printf("No Road\n");
					break;
				}
				
			}
		}
		for (int k = 0; k < pos_i + 1; k++)
			printf("(%d,%d)\n", pos_x[k], pos_y[k]);
	}
}