非门=与非门+与非门=2个与非门
或门=非门+非门+与非门=3个与非门
与门等于与非门加非门=3个与非门
异或门等于((非门+与非门)+(非门+与非门))+非门=5个与非门
有版本的意思的4个与非门就可以实现异或门
下图是与门,有点错F=A*B= 。。。

下图是或门

下图这个是说是可以四个与非门构成的异或门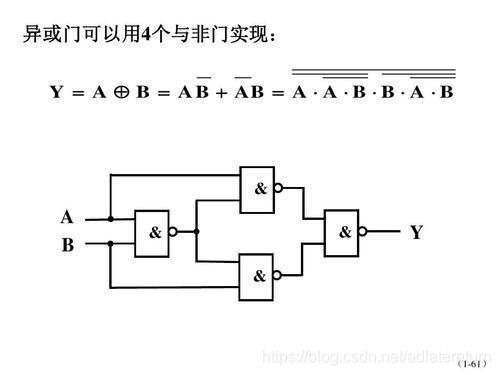
然而课堂上老师要求的异或门: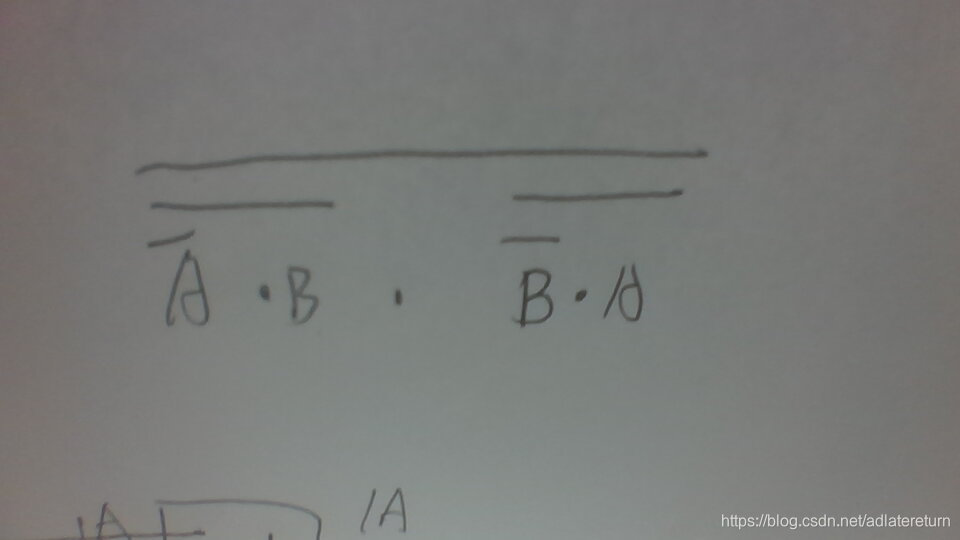
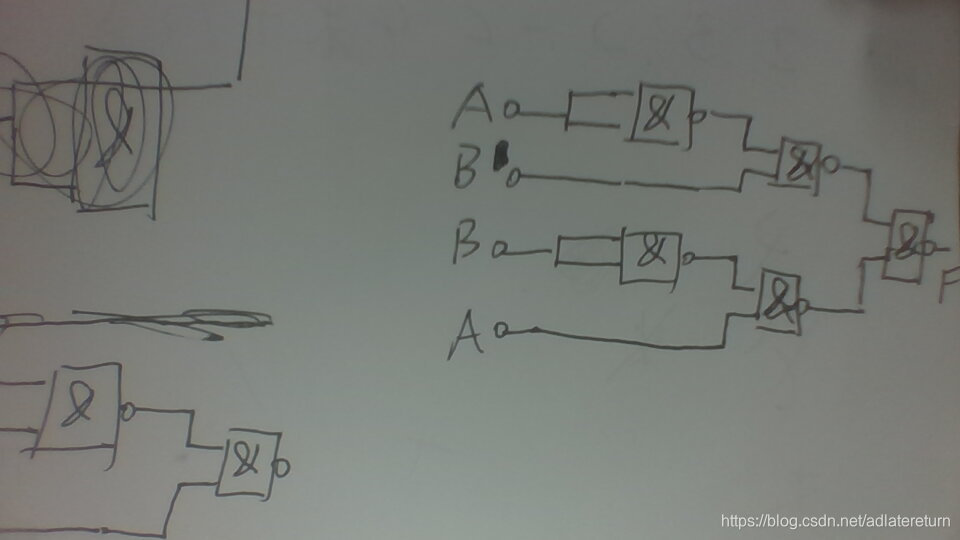
可见条条大路通罗马
 本文探讨了如何仅使用与非门构建各种基本逻辑门,包括非门、或门、与门和异或门。文章详细说明了构建过程,并指出通过不同组合,最少只需2个与非门即可实现非门,而异或门则需至少4个与非门。这一主题深入到数字逻辑设计的基础,展示了逻辑门之间的转换和组合艺术。
本文探讨了如何仅使用与非门构建各种基本逻辑门,包括非门、或门、与门和异或门。文章详细说明了构建过程,并指出通过不同组合,最少只需2个与非门即可实现非门,而异或门则需至少4个与非门。这一主题深入到数字逻辑设计的基础,展示了逻辑门之间的转换和组合艺术。
非门=与非门+与非门=2个与非门
或门=非门+非门+与非门=3个与非门
与门等于与非门加非门=3个与非门
异或门等于((非门+与非门)+(非门+与非门))+非门=5个与非门
有版本的意思的4个与非门就可以实现异或门
下图是与门,有点错F=A*B= 。。。

下图是或门

下图这个是说是可以四个与非门构成的异或门
然而课堂上老师要求的异或门: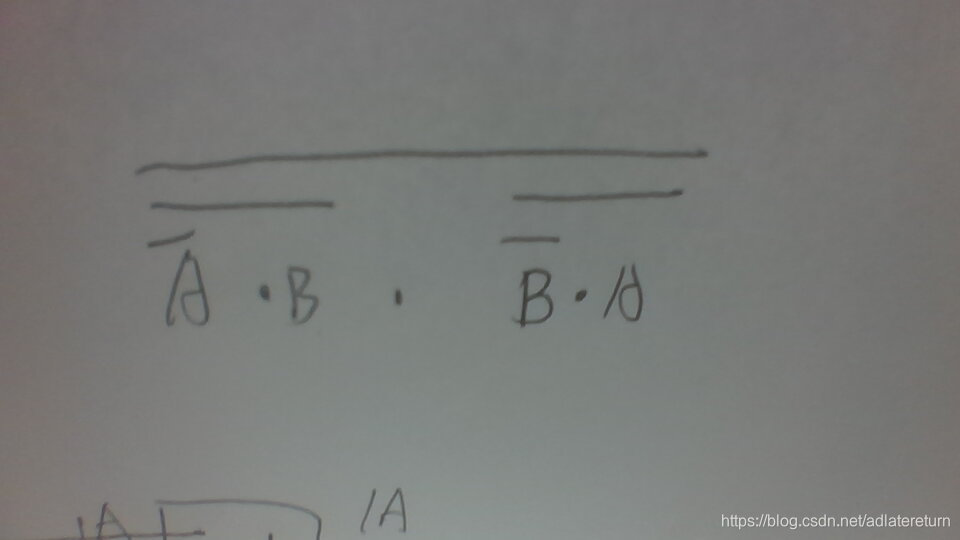

可见条条大路通罗马
 5370
5370
