http://noi.openjudge.cn/——4.3算法之图论——253:丛林中的路

题目

253:丛林中的路
总时间限制: 1000ms 内存限制: 65536kB
描述

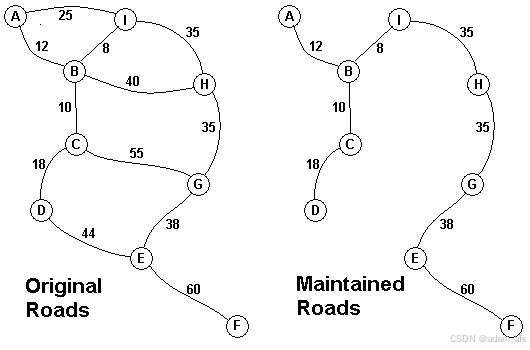
热带岛屿Lagrishan的首领现在面临一个问题：几年前，一批外援资金被用于维护村落之间的道路，但日益繁茂的丛林无情的侵蚀着村民的道路，导致道路维修开销巨大，长老会不得不放弃部分道路的维护。上图左侧图显示的是正在使用道路的简图以及每条路每个月的维修费用（单位为aacms）。现在长老会需要提出一种方案，即需要保证村落之间都可以互相到达，又要将每个月的道路维修费用控制在最小。村子编号为从A到I。上图右侧显示的方案最小维修开销为216 aacms每月。

输入
输入包含1~100个数据集，最后一行为0.每个数据集第一行为村落数目n, 1 < n < 27,依次用字母表的前n个字母标记。接下来有n-1行，每行的第一个数据便是按字母顺序排列的村子编号（不包括最后一个村庄）。每个村庄后面的数据k代表该村庄通往编号在其之后的村庄的道路数目，如A 2 B 12 I 25，代表A村庄有2个编号在A之后的村庄和其相连。若k大于0，k后面会依次给出这k个村庄的编号以及各自到起始村庄的道路维修费用，如A 2 B 12 I 25，代表A和B之间道路维修费用为12， A和I之间道路维修费用为25（维修费用为不超过100的正整数）.路的总数目不超过75条，每个村庄到其他村庄不会有超过15条路（包括编号在其之前和之后的）。
输出
每个数据集有一个输出：针对解决方案每个月维修道路的小费用。
提示：蛮力算法虽能找出解决方案，但将会超出时间限制。
样例输入
9
A 2 B 12 I 25
B 3 C 10 H 40 I 8
C 2 D 18 G 55
D 1 E 44
E 2 F 60 G 38
F 0
G 1 H 35
H 1 I 35
3
A 2 B 10 C 40
B 1 C 20
0
样例输出
216
30

思路

Kruskal 算法，用于解决最小生成树（Minimum Spanning Tree, MST）问题。
在连通图中选择权值最小的边，连接所有节点，且不形成环路，最终总权值最小。
排序所有边：按权值从小到大排序。
贪心选择边：依次选择权值最小的边。
避免环路：使用并查集（DSU）判断边的两个端点是否属于同一集合。
若属于不同集合，合并两个集合，并累加边权值。
若属于同一集合，跳过该边（避免环路）。

代码

#include <bits/stdc++.h>
using namespace std;
struct node{
	int x,y;//道路两端的村庄 
	int dis;//道路维修费用 
	char cx,cy;
	bool operator<(node b){
		return dis<b.dis;
	}
}road[100];
struct point{
	int f,//父节点 
		num;//集合大小 
}f[30];
int n;//村庄数 
void view(int m){
	for(int i=1;i<m;i++)cout<<road[i].cx<<","<<road[i].cy<<"="<<road[i].dis<<"\t";cout<<endl;
	for(int i=1;i<m;i++)cout<<char(f[road[i].x].f+'A')<<","<<char(f[road[i].y].f+'A')<<"\t";cout<<endl;
}
int find(int x){
	if(x==f[x].f)return x;//父节点是自身时返回根 
	return f[x].f=find(f[x].f);//否则递归查找根节点，回溯时沿途节点的父节点都是根（路径压缩，实现扁平化） 
}
bool he(int x,int y){
	int fx=find(x),//两件事，1找到根，2实现沿途节点的父节点的设置 
		fy=find(y);
	if(fx==fy)return 0;//父一样，说明已经联通，不需该道路 
	if(f[fx].num>=f[fy].num)f[fy].f=fx,f[fx].num+=f[fy].num;
	else f[fx].f=fy,f[fy].num+=f[fx].num;
	//根据两个集合大小完成，大的吞并小的
	//新加入村庄父节点的设置得等下次调用fuind()时更新 
	return 1;
} 
int main(){
	freopen("data.cpp","r",stdin);
	while(cin>>n&&n){
		int road_n=1,//多少条边 
			m,//出发几天路 
			dis,//距离
			x,y,
			ans=0;//多组初始化 
		char cx,cy;//从哪里出发，到哪里 
		for(int i=1;i<n;i++){//共几个出发村 
			cin>>cx>>m;x=cx-'A';
			f[x]=point{x,1};//父是自己 
			for(int j=0;j<m;j++){//从该村出发有几条路 
				cin>>cy>>dis;y=cy-'A';
				road[road_n++]=node{x,y,dis,cx,cy};//端点一大的 
				f[y]=point{y,1};//父是自己 
			}
		}
		//贪心算法，先选择最小费用的两个村庄进行合并并查集(DSU)
		//kruskal算法:解决最小生成树（Minimum Spanning Tree, MST）问题,
		sort(road+1,road+road_n);//所有道路根据费用排序 
		//view(road_n); 
		//最短路的两个端点分别有各自的方案，所以归并到第一个端点方案中，添加路 
		for(int i=1;i<road_n;i++){
			if(he(road[i].x,road[i].y)){//如果是两个集合就合并，并增加该道路的费用。否则跳过，避免闭环 
				ans+=road[i].dis;
				view(road_n);
			}else cout<<"no\n";
			cout<<road[i].cx<<","<<road[i].cy<<"="<<ans<<endl;
		}
		//view(road_n); 
		cout<<ans<<endl;
	}
	return 0;
}

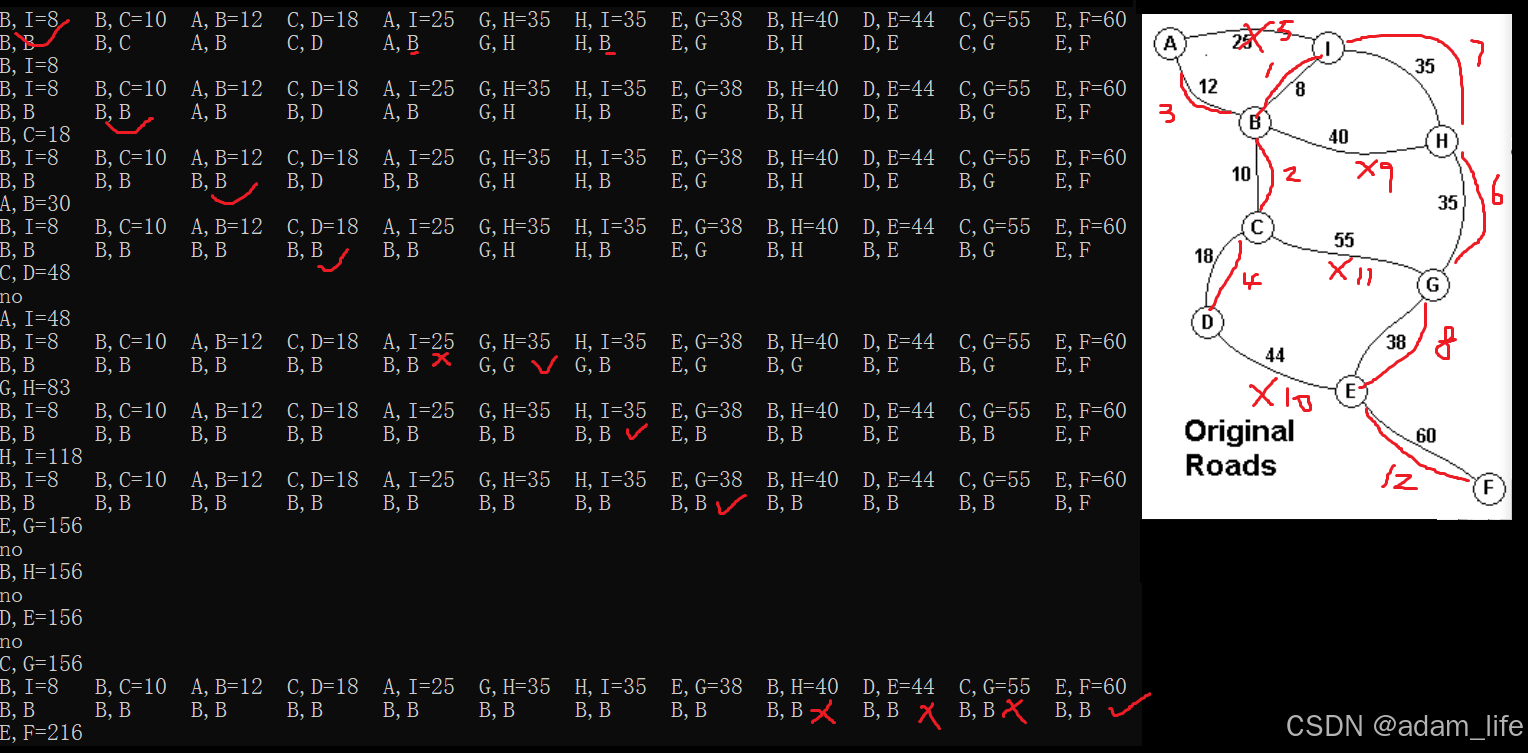
过程