PAT 1007 Maximum Subsequence Sum 用例5不能通过

动态规划解决子序列最大和问题及超时用例修复

最新推荐文章于 2025-12-01 22:16:11 发布

原创最新推荐文章于 2025-12-01 22:16:11 发布 · 168 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #动态规划

PAT 专栏收录该内容

1 篇文章

订阅专栏

博客讲述了在处理一个寻找数组中子序列最大和的问题时，遇到的最后一个用例超时的情况。作者首先尝试了穷举所有子序列的方法，但因效率低下导致超时。接着，作者转向使用动态规划进行优化，通过一个三维数组dp存储子序列信息。在初始化和迭代过程中，特别处理了全负数数组的情况，以确保正确输出。尽管如此，用例5仍然无法通过，可能的原因是对于特定情况的判断不充分。博客提供了具体的代码片段和思路解析，帮助读者理解动态规划在解决此类问题中的应用。

1.最后一个用例运行超时

我一开始使用了穷举子序列个数和所有的子序列，但是最后一个用例超时了。

所以采用时间上更合理的动态规划

用dp[k+1][3]存含当前数的最大和子序列信息，dp[i][0]存子序列最大和，dp[i][1]存子序列开始下标+1,dp[i][2]存子序列结束下标+1（其实就是i，也可以优化掉，弄一个两行的二维数组）

dp[0][0]=0;dp[0][1]=0;dp[0][2]=0;//设置边界条件
    for(int i=1;i<k+1;i++){    //i指的是第几个数，不是下标，下标还要初始化
        dp[i][0]=figures[i-1];    //对每个策略初始化为当前数
        dp[i][1]=i;                //对策略下标初始化
        dp[i][2]=i;
        if(dp[i-1][0]>0){        //dp迭代
            dp[i][0]=figures[i-1]+dp[i-1][0];
            dp[i][1]=dp[i-1][1];
        }
    }

2.用例5始终不能通过

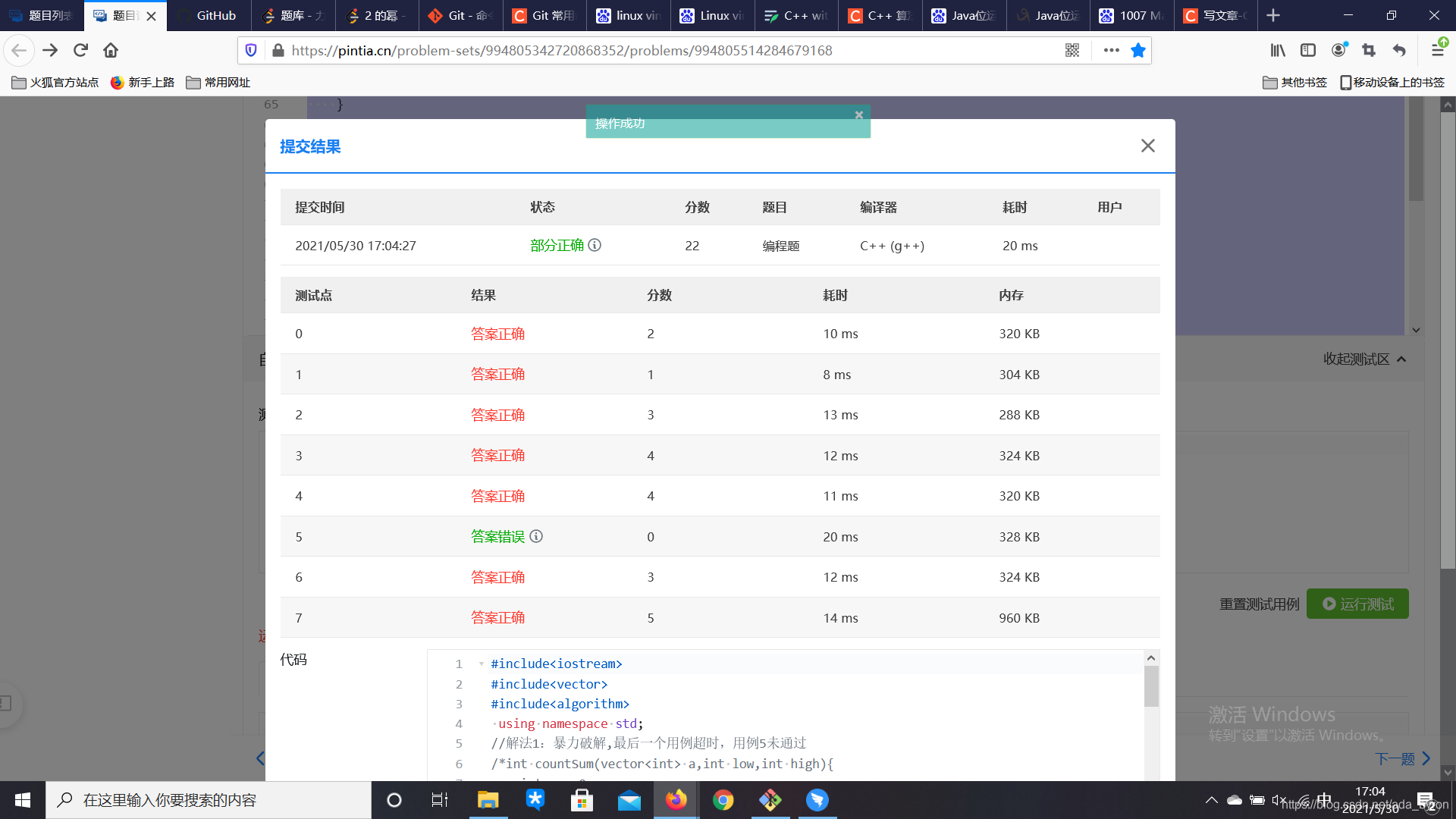
先解释以下：用例5应该是有一个数为0，其他数为负数的用例

例如：-1，-2，0，-3，-4

由于题目要求全是负数时，输出是：0，数组的第一个数，数组的最后一个数

所以大家初始化的时候可能会用全是负数的默认条件，解决方法是当dp[i][0](含i项的最大和)等于maxSum（最大和）的时候，看谁的第二个下标更小，然后更新下标

if(dp[i][0]==maxSum){
            if(dp[i][2]-1<last){
            first=dp[i][1]-1;
            last=dp[i][2]-1;}
        }