Luogu P3618 误会

题目本身不难，只是一个线性递推的问题。

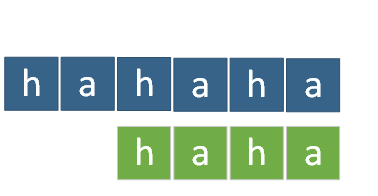
设$f(i)$为读取到A字符串的第i位时，一共有多少种读取意思。
转移情况有两种：
1.当A字符串的第i位匹配不上B字符串时，$f(i)=f(i-1)$
2.当A字符串的第i位匹配上B字符串时，$f(i)=f(i-m)+f(i-1)$
例子中$f(6)=f(2)+f(5)=1+1=2$
初始化边界$f(0)=1$

匹配可以用两种方法来做
Hash的方法

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef vector<int> vi;
typedef vector<ll> vll;
typedef unsigned long long ull;

const int N = 100010;
int n, m;
char a[N];
char b[N];

ull ha[N], hb;
ll p = 13131;
ll pw;
ll f[N];
ll mod = 1e9 + 7;

void solve(int idx) {
	scanf("%s", a + 1);
	scanf("%s", b + 1);
	n = strlen(a + 1), m = strlen(b + 1);
	for(int i = 1; i <= n; ++ i) {
		ha[i] = ha[i - 1] * p + a[i];
	}
	pw = 1;
	for(int i = 1; i <= m; ++ i) 
		pw *= p;
	hb = 0;
	for(int i = 1; i <= m; ++ i) {
		hb = hb * p + b[i];
	}
	f[0] = 1;
	for(int i = 1; i <= n; ++ i) {
		f[i] = f[i - 1];
		if(i >= m) {
			ull h0 = ha[i] - (ha[i - m]) * pw;
			if(h0 == hb) {
				f[i] = (f[i] + f[i - m]) % mod;
			}
		} 
	}
	printf("Case #%d: %lld\n", idx, f[n]);
}


int main(){
//	freopen("in.txt", "r", stdin);
	int t;
	scanf("%d", &t);
	for(int i = 1; i <= t; ++ i) {
		solve(i);
	}
	return 0; 
}

Kmp的方法

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef vector<int> vi;
typedef vector<ll> vll;
typedef unsigned long long ull;

const int N = 100010;
int n, m;
char a[N];
char b[N];
ll f[N];
ll mod = 1e9 + 7;
int nxt[N];
bool match[N];

void get() {
	nxt[1] = 0;
	for(int i = 2, j = 0; i <= m; ++ i) {
		while(j > 0 && b[i] != b[j + 1])
			j = nxt[j];
		if(b[i] == b[j + 1])
			j ++;
		nxt[i] = j;
	}
}


void kmp() {
	for(int i = 1, j = 0; i <= n; ++ i) {
		while(j > 0 && a[i] != b[j + 1]) 
			j = nxt[j];
		if(a[i] == b[j + 1])
			j ++;
		if(j == m) {
			match[i] = 1;
			j = nxt[j];
		}else {
			match[i] = 0;
		}
	}
}


void solve(int idx) {
	scanf("%s%s", a + 1, b + 1);
	n = strlen(a + 1), m = strlen(b + 1);
	get();
	kmp();
	f[0] = 1;
	for(int i = 1; i <= n; ++ i) {
		f[i] = f[i - 1];
		if(match[i]) {
			f[i] = (f[i] + f[i - m]) % mod;
		}
	}
	printf("Case #%d: %lld\n", idx, f[n]);
}


int main(){
//	freopen("in.txt", "r", stdin);
	int t;
	scanf("%d", &t);
	for(int i = 1; i <= t; ++ i) {
		solve(i);
	}
	return 0; 
}