EXOCENTER OF A TRIANGLE
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 3532 | Accepted: 1413 |
Description
Given a triangle ABC, the Extriangles of ABC are constructed as follows:
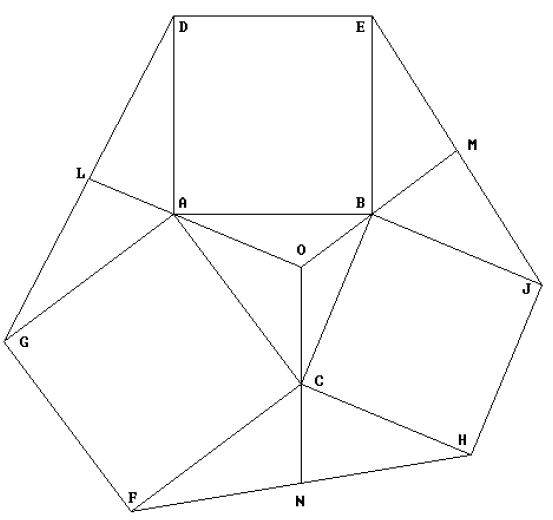
On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below).
Connect adjacent square corners to form the three Extriangles (AGD, BEJ and CFH in the figure).
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure).
This problem is to write a program to compute the Exocenters of triangles.
On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below).
Connect adjacent square corners to form the three Extriangles (AGD, BEJ and CFH in the figure).
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure).
This problem is to write a program to compute the Exocenters of triangles.

Input
The first line of the input consists of a positive integer n, which is the number of datasets that follow. Each dataset consists of 3 lines; each line contains two floating point values which represent the (two -dimensional) coordinate of one vertex of a triangle. So, there are total of (n*3) + 1 lines of input. Note: All input triangles wi ll be strongly non-degenerate in that no vertex will be within one unit of the line through the other two vertices.
Output
For each dataset you must print out the coordinates of the Exocenter of the input triangle correct to four decimal places.
Sample Input
2 0.0 0.0 9.0 12.0 14.0 0.0 3.0 4.0 13.0 19.0 2.0 -10.0
Sample Output
9.0000 3.7500-48.0400 23.3600
证明过程转自:http://www.2cto.com/kf/201411/348474.html
∵AK = A'K DK = GK ∠6 = ∠7
根据(SAS) ∴△AGK≌A'GK
∴∠1 = ∠4
又∵∠1 + ∠2 + ∠3 = 180°
∴∠2 + ∠3 + ∠4 = 180°
又∵∠3 + ∠4 + ∠5
∴∠2 = ∠5
又∵AD = AB AG = AC
根据SAS ∴△ABC≌DAA'
∴∠3 = ∠8
又∵∠BAO + ∠3 = 90°
∴∠BAO + ∠8 = 90°
∴∠9 = 90°
同理∠10 = ∠11 = 90°
∴点O为高线交点 为△ABC的垂心
证毕。
代码分为两个,一个是比较麻烦的用斜率处理(特殊情况较多),另一个是用来自数学吧大神的结论写的。
代码一:
代码二:struct Point { double x,y; }; int main() { int T; Point a,b,c,d;///abc三点是顶点,d是垂心 double k,k1,kk,kk1,b1,bb1;///ab边的斜率,垂直于ab边的斜率,ac边的斜率,垂直于ac边的斜率,y=kx+b中的b int flag,flag1;///标记ab边和ac边是否是水平边(水平边斜率为0,垂直于水平边的直线斜率不存在。) scanf("%d",&T); while(T--) { flag=flag1=0; scanf("%lf %lf",&a.x,&a.y); scanf("%lf %lf",&b.x,&b.y); scanf("%lf %lf",&c.x,&c.y); if(b.x==a.x) k1=0;///如果ab边是垂直边,那么直接得出垂直于ab边的直线斜率为0 else if(b.y==a.y) flag=1;///ab边是水平边,标记一下。 else { k=(b.y-a.y)/(b.x-a.x); k1=-1/k; } if(c.x==a.x) kk1=0; else if(c.y==a.y) flag1=1; else { kk=(c.y-a.y)/(c.x-a.x); kk1=-1/kk; } if(flag) { d.x=c.x;///如果ab边是水平边,那么垂心的x坐标肯定和c点x坐标一样 bb1=b.y-kk1*b.x; } else if(flag1) { d.x=b.x; b1=c.y-k1*c.x; } else { b1=c.y-k1*c.x; bb1=b.y-kk1*b.x; d.x=(bb1-b1)/(k1-kk1); } if(flag) d.y=kk1*d.x+bb1; else d.y=k1*d.x+b1; printf("%.4lf %.4lf\n",d.x,d.y); } return 0; }#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> using namespace std; #define eps 1e-8 struct Point { double x,y; }; double method(Point a,Point b,Point c) { return (a.x-c.x)*(b.x-c.x)+(a.y-c.y)*(b.y-c.y); } double dist(Point a,Point b) { return sqrt((b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y)); } int main() { int T; Point a,b,c,d; double ab,ac,bc,cosA,cosB,cosC; double q,w,e; scanf("%d",&T); while(T--) { scanf("%lf %lf %lf %lf %lf %lf",&a.x,&a.y,&b.x,&b.y,&c.x,&c.y); if(fabs(method(b,c,a))<eps)///判断是否存在直角,如果存在垂心为直角点 printf("%.4lf %.4lf\n",a.x,a.y); else if(fabs(method(a,c,b))<eps) printf("%.4lf %.4lf\n",b.x,b.y); else if(fabs(method(a,b,c))<eps) printf("%.4lf %.4lf\n",c.x,c.y); else { ab=dist(a,b); ac=dist(a,c); bc=dist(b,c); cosA=(ac*ac+ab*ab-bc*bc)/(2*ac*ab); cosB=(bc*bc+ab*ab-ac*ac)/(2*bc*ab); cosC=(bc*bc+ac*ac-ab*ab)/(2*bc*ac); q=bc/cosA;w=ac/cosB;e=ab/cosC; d.x=(q*a.x+w*b.x+e*c.x)/(q+w+e); d.y=(q*a.y+w*b.y+e*c.y)/(q+w+e); printf("%.4lf %.4lf\n",d.x+eps,d.y+eps);///会出现-0.000要加eps } } return 0; }





 本文介绍了一种计算三角形外心的方法,通过构造三角形的扩展三角形并找到其共通交点即外心。提供了两种实现代码,一种基于斜率处理特殊情况,另一种则依据数学原理简化了计算过程。
本文介绍了一种计算三角形外心的方法,通过构造三角形的扩展三角形并找到其共通交点即外心。提供了两种实现代码,一种基于斜率处理特殊情况,另一种则依据数学原理简化了计算过程。

















 513
513










