回归和分类算法

回归和分类算法

A-线性回归算法：

如工资预测：

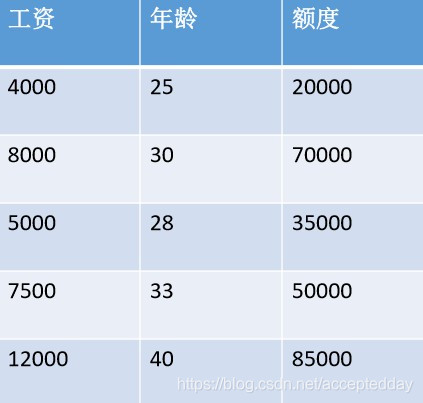
（01）线性回归的公式：

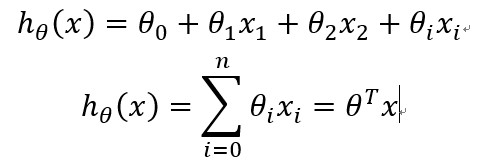
（02）线性回归误差分析：

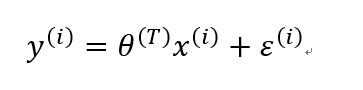
如上为线性回归误差公式。

条件：（1）样本预测结果相互独立。（2）样本预测结果处于于相同的误差范围。（3）均值为0，且方差为θ∧2的正态分布（高斯分布），得到如下公式（μ=0）：

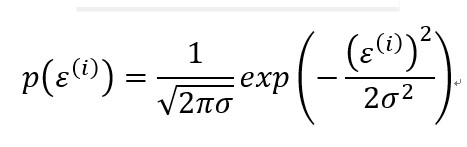
然后通过对ε(i)进行替换，得到如下的式子：

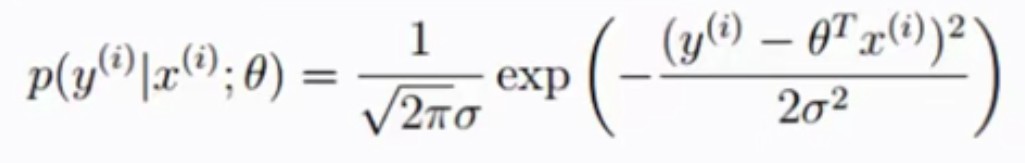
（注释：某θ值与x拟合后得到p(x;θ)越接近于p(y)。）

（03）引入似然函数：

（目的：对全体样本进行预测估计）

针对不同的θ值=》L(θ)数值=》取max值时的θ向量组即为θ的最终理想解。（m为样本总数。）

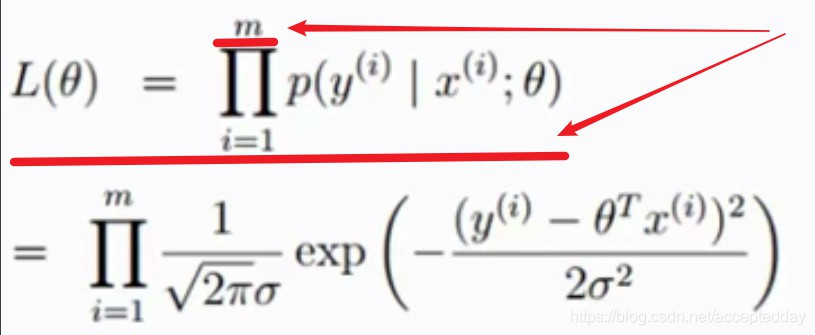
（04）引入对数似然函数：

目的：将乘法计算过程转换为加法计算过程。

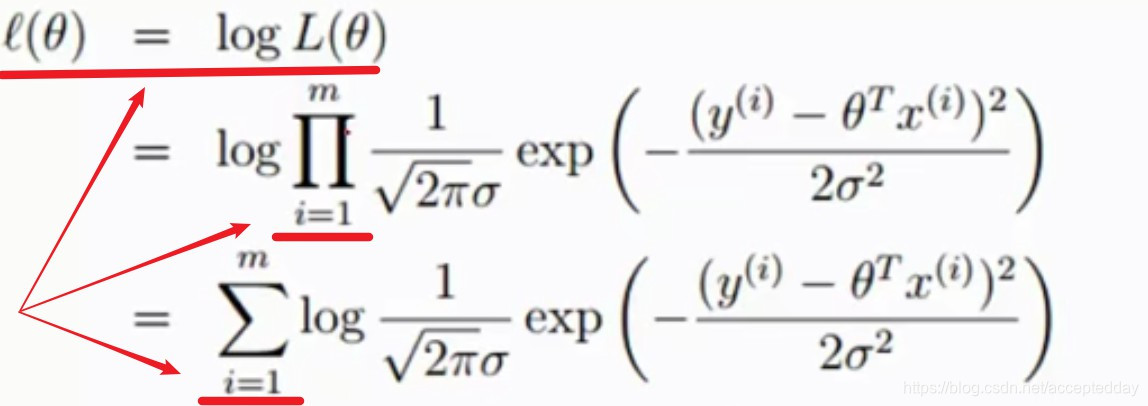
然后进行化简得到下式。

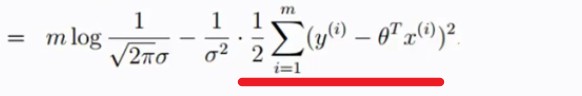
得到目标函数如下：

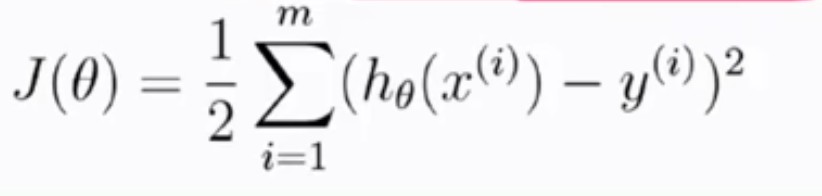
(05)行列式的计算：

对目标函数进行行列式的转换求解，如下：

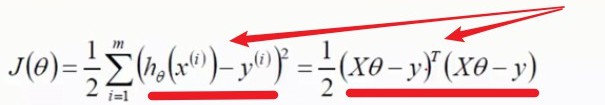
（定理运用：a∧2=a∧T*a）

对J(θ)求导，进行极值的计算如下：

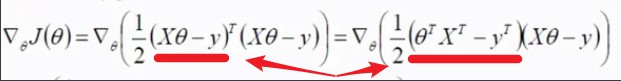
（定理运用：（ab+c）∧T=b∧T*a∧T+c∧T）

(06)行列式的求导：

进行求导的过程如下：

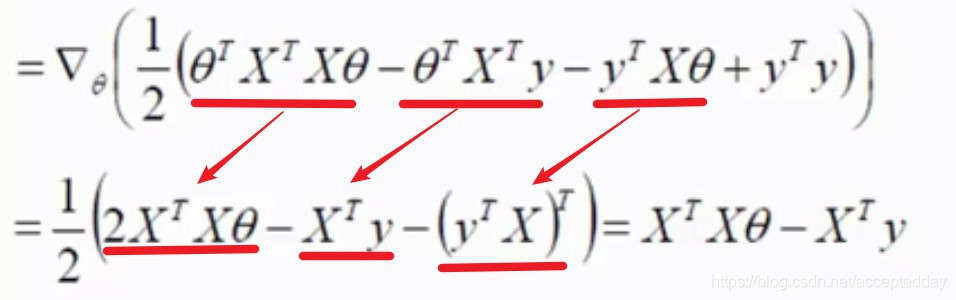
（定理运用：行列式求导知识）

令▽θJ(θ)=0，得到θ的理想解：

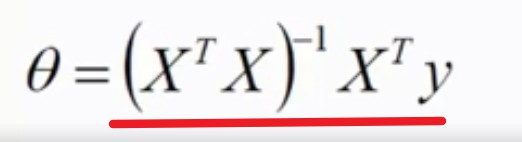
B-logistic回归算法：

（01）引入sigmoid函数：

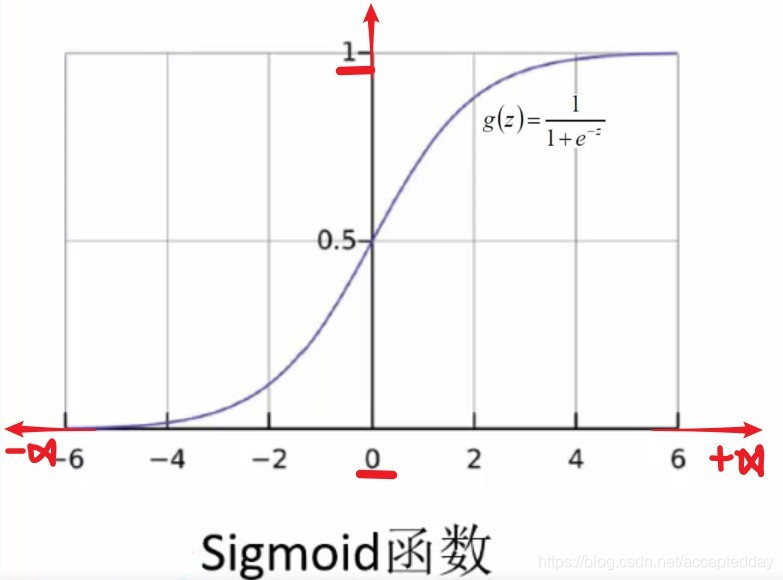
以(θ∧T*X)为自变量得到下式：

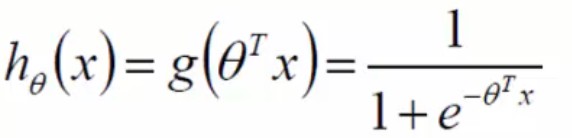
(*)应用一分类：

然后根据 θ∧T得到相应的hθ(x)值，然后根据设定的概率区间对X进行分类。

(*)应用二理想解：

若θ∧T为未知理想解，使得hθ(x)趋近于0/1，则对g(θ∧T*x)进行求导，求其极值点，得到如下关系式：

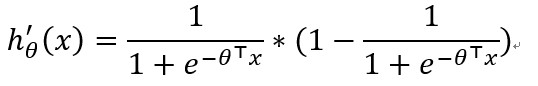
C-梯度下降原理：

(*)实例分析：

(01)Normalize the data:

(02)J(θ0,θ1)线性关系的分析：

假设y与x为线性回归关系：

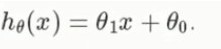
(03)根据线性回归的误差分析，得到代价函数：

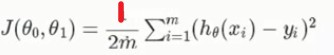
代码实现部分：

测试样例：

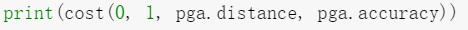
(04)根据线性回归分析特点，对θ1和θ0求偏导式如下：

θ1：

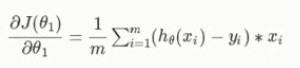
θ0：

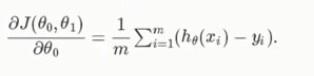
代码实现部分：

θ1：

θ0：

测试样例：

θ1：

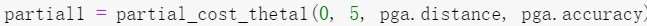
θ0：

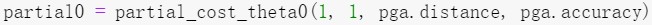
(05)引入“梯度”概念：

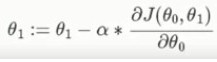
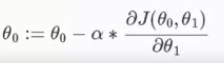
如图：
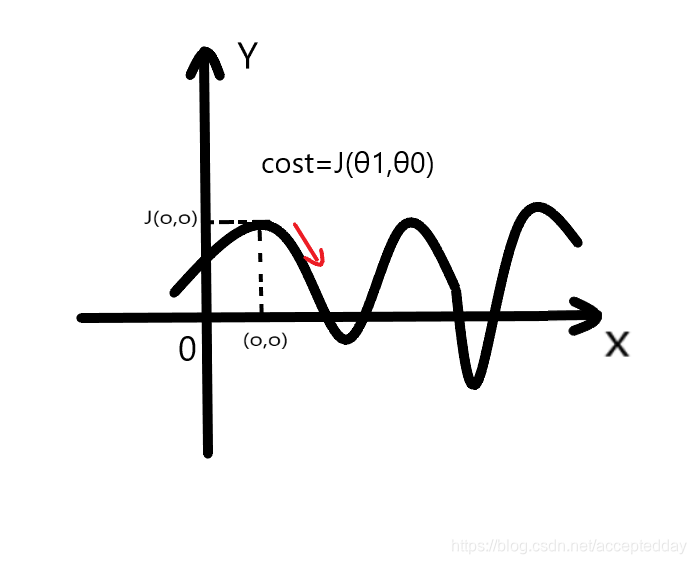如图为cost=J(θ1,θ0)示意图(cost大于0，图示有误)。α为设定的步长，∂J(θ0,θ1)/∂θ0为梯度。

(06)设定边界值训练：

α，θ1，θ0，max_epochs,convergence_thres,cprev的设定和初始化采用预设值。

代码部分：

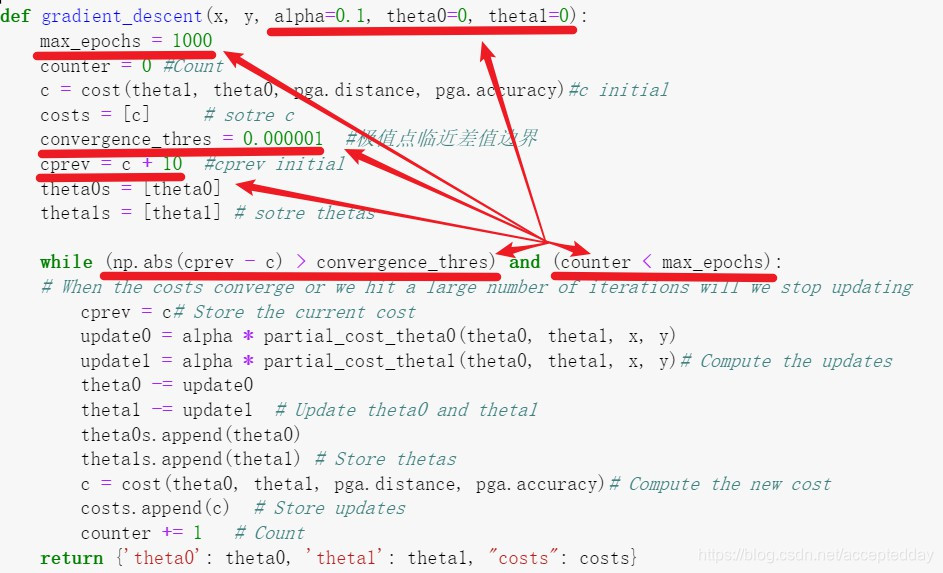
测试样例：

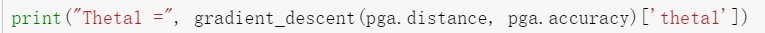
（07）cost与训练次数分析：

最优解样例：

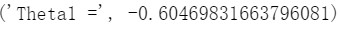
附cost与训练次数关系图：