并查集解决除法求值（这竟然是medium难度！！）

今天做到了一题除法求值：

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。
注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/evaluate-division

这题竟然是medium，离谱。我只想说hard，hard！

宽度优先搜索

每一对数有不同的值，题目说明了“每个 Ai 或 Bi 是一个表示单个变量的字符串。”我的第一解题思路是构建带权值的有向图。将问题模型给构建出来。然后对于每个queries[i] 我只需在图中寻找是否有该路径可以得到这个结果。如果没有答案就用 -1.0替代。
这题想通了其实倒是不难。重点是转化为有向图。为了方便搜寻，我们对equations的顺序进行编号来作为我们的节点。

class Pair{
    int index; // equations变量的编号
    double value; //value[i] 可以当做权值

    public Pair(int index, double value) {
        this.index = index;
        this.value = value;
    }
}

那么出现的 a / b = 2 就可以构建两个 Pair节点： {0, 2} 和 {1, 0.5};那么很轻松的（艰难的）就可以构建我们的带权值的有向图了。

 Map<String, Integer> hashMap = new HashMap<>();
        int id = 0;
        for(int i = 0; i < equationsSize; i++) {
            List<String> equation = equations.get(i);
            String str1 = equation.get(0);
            String str2 = equation.get(1);
            if(!hashMap.containsKey(str1)) {
                hashMap.put(str1, id++); // 存储id 也就是后面的index值 方便后续遍历
            }
            if(!hashMap.containsKey(str2)) {
                hashMap.put(str2, id++);
            }
        }
        // 构建邻接矩阵
        List<Pair>[] edges = new List[id]; 
        for(int i = 0; i < id; i++) {
            edges[i] = new ArrayList<>();
        }
        for(int i = 0; i < equationsSize; i++) {
            List<String> equation = equations.get(i);
            String str1 = equation.get(0);
            String str2 = equation.get(1);
            //  例如{0, 2} 和 {1, 0.5}
            edges[hashMap.get(str1)].add(new Pair(hashMap.get(str2), values[i]));
            edges[hashMap.get(str2)].add(new Pair(hashMap.get(str1), 1.0/values[i]));
        }

接下来就好多了 不就搜寻有向图嘛， 方法多多， dfs，bfs，Floyd…
这里我用的bfs 感觉好写一点。

		int n = queries.size();
        double[] res = new double[n];
        for(int i = 0; i < n; i++) {
            List<String> tmp = queries.get(i);
            double result = -1.0;
            // 判断是否存在这个组合的问题
            if(hashMap.containsKey(tmp.get(0)) && hashMap.containsKey(tmp.get(1))) {
                int id1 = hashMap.get(tmp.get(0)), id2 = hashMap.get(tmp.get(1));               
                if(id1 == id2) {
                   result = 1.0;
                } else {
                	//我们在搜寻的同时标记我们标记了的位置，剪枝并且避免死循环
                    Queue<Integer> queue = new LinkedList<>();
                    queue.offer(id1);
                    double[] arr = new double[id];
                    Arrays.fill(arr, -1.0);
                    arr[id1] = 1.0;
                    while(!queue.isEmpty() && arr[id2] < 0) {
                        int cur = queue.poll();
                        // 边走边对value值更新 
                        for(Pair pair : edges[cur]) {
                            int next = pair.index;
                            double val = pair.value;
                            if(arr[next] < 0) {
                                arr[next] = arr[cur] * val;
                                queue.offer(next); 
                            }
                        }
                    }
                    result = arr[id2];
                }
            }
            res[i] = result;
        }

这个问题就解决了，撒花。

瞅了瞅题解，带权值得并查集来解决这道题。

并查集

除数组对应的value之间有了倍数关系。所以我就建立了带权值的有向图；由于变量之间的倍数关系具有传递性，处理有传递性关系的问题，可以使用「并查集」，我们需要在并查集的「合并」与「查询」操作中 维护这些变量之间的倍数关系。

并查集的两个主要操作： 合并Union与查询Find
在这之前，我们对这些节点进行初始化， 我们将每个节点定义为：

private int[] parent; // 指向的父亲节点
private double[] weight; // 权值 会随着路径压缩而改变

查询Find

查询主要功能就是从某个节点向上遍历找到根节点，那么时间复杂度就是树高。但是这样有了极端情况，那就是树成了链表，这样是极不友好的。并查集中的查询使用到了路径压缩，针对树高进行了优化。
路径压缩的效果是：在查询一个结点 a 的根结点同时，把结点 a 到根结点的沿途所有结点的父亲结点都指向根结点。除了根结点以外，所有的结点的父亲结点都指向了根结点。而且最大的优点是是在查询的时候优化，我们并不需要刻意的去维护这个高度为1的树。

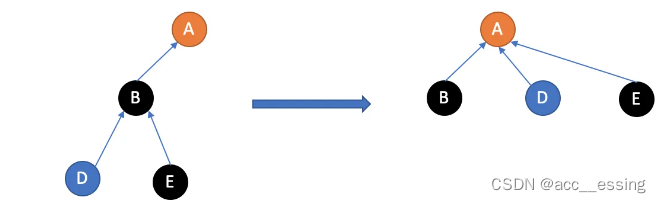
初始化时所有节点的父亲节点都指向自己，在构建过程中逐渐构建成了上图左边所示，那么只有根节点的父亲节点指向自己。所以 我们可以这样定义Find（）方法。

  public int find(int x) {
            if (x != parent[x]) {
                int origin = parent[x];
                parent[x] = find(parent[x]);
                weight[x] *= weight[origin];
            }
            return parent[x]; 
        }

这样每次查询时，就可以将从x 到跟节点路径压缩。惊艳！！！

合并Union

如果两个节点是连通的（传递），那么就可以将两个节点的父节点合并。合并完之后肯定不是树高为1了。那后续计算边的权值就是错误的啊。
但是考虑查询后就不会了，计算权值时我们首先得查询，那么查询执行的过程中就把这个集合（树）路径压缩， 这可真是太巧妙了噢！

  public void union(int x, int y, double value) {
            int rootX = find(x);
            int rootY = find(y);
            //将有联系的两个节点的父亲节进行合并
            if (rootX == rootY) {
                return;
            }
            parent[rootX] = rootY;
            // 因为 weight[rootX] * weight[x] = weight[y] * value
            weight[rootX] = weight[y] * value / weight[x];
        }

并查集有了平衡优化那么解题效率就大大提高了。

又学到了好玩的东西，并查集的特点就是边查询边优化。
总结下并查集：

1. 这个集合中用parent数组记录每个节点的父节点，用weight 数组记录权值，这是会随着查询或者合并过程中随时修改的。（如果不是带权值的有向图就不需要这个weight数组，LeetCode题解后面有很多链接练习）初始化时将父亲节点就是本身。
2. 将所有点的联系加入到这个并查集中，这时它肯定不是压缩了的，但是一旦开始查询就能在这个过程中保证树的高度，使得后续的计算（不管是权值，还是其他判断）都能保证时间为O(1) 。
3. 后续就是在集合中查询节点的联系来求解即可。

题目链接 ：399. 除法求值