单调栈解决柱状图及引申问题

84 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。
如图：

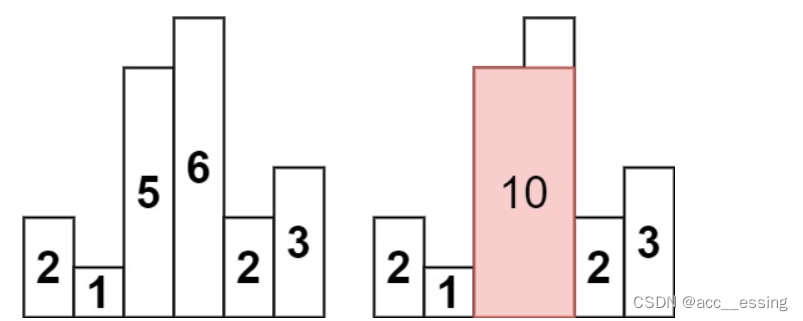
这题乍一看我都以为是动态规划，但是仔细分析发现好像最优子结构并不适合状态转移。那么思路可能就是穷举：
1） 枚举宽w，那么就是一个二重循环来确定，对每个循环中找出相应最矮的那个柱子，那么就是对应的最大矩阵。
2）枚举高h，通过向左右延伸找到比它更小的高度值，就是该高度对应的最大矩阵。
穷举一下时间复杂度高达O(m * n)， 那估计是要超时了。
进一步思考，对于枚举高度hi，我们向左右延伸时找到左右两侧最近的高度小于 h 的柱子，这样这两根柱子之间（不包括其本身）的所有柱子高度均不小于 h，并且就是 i能够扩展到的最远范围。

对于两根柱子i, j ，高度i是大于高度j的，那么在j之后出现的柱子一定不会以i作为它的左边界。那么我们只需维护一组递增数，当对于当前枚举的高度在这组数中向前找到第一个比他小的即可。

一组递增序列的维护肯定就是单调栈了：
单调栈可以分为递增单调栈以及递减单调栈，对于到来的数pop比他大/小的值，再将其push进栈。

 for(int i = 0; i < n; i++) {
            while(!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
                stack.pop();
            }
            stack.push(i);
        }
// --------------------------------------------------------------
 for(int i = 0; i < n; i++) {
            while(!stack.isEmpty() && arr[stack.peek()] <= arr[i]) {
                stack.pop();
            }
            stack.push(i);
        }

那么对于上面这题解决就很方便了，只需对于枚举的高度，找出其对应的左边界；再以同样的方法获得其有边界。

public int largestRectangleArea(int[] heights) {
        int n =heights.length;
        int[] left = new int[n];
        int[] right = new int[n];
		// LinkedList当栈使用
        Deque<Integer> stack = new LinkedList<>();
        for(int i = 0; i < n; i++) {
            while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
                stack.pop();
            }
            left[i] = (stack.isEmpty() ? -1 : stack.peek());
            stack.push(i);
        }
        stack.clear();
        for(int i = n - 1; i >= 0; i--) {
           while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
               stack.pop();
            }
            right[i] = stack.isEmpty() ? n : stack.peek();
            stack.push(i);
        }
        int res = 0;
        for(int i = 0; i < n; i++) {
            int sum = (right[i] - left[i] - 1) * heights[i];
            res = Math.max(res, sum);
        }
        return res;
    }

85 最大矩形

再看一题，给定一个二维矩阵由0,1组成，要找出其中最大的由 1 组成的矩阵。

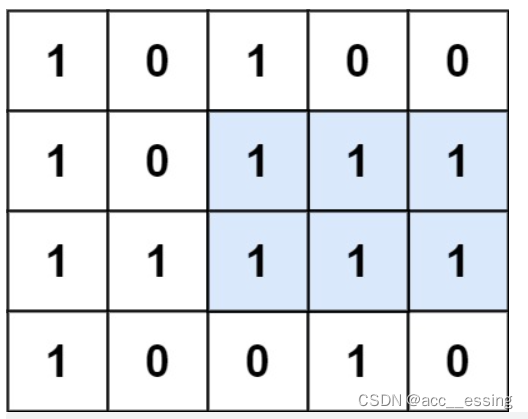
在一个二维下，找出最大矩阵，用柱状图的方法是可以解决的。
那又该以什么作为“高”来枚举呢？
对于每行的“1”我们可以将其连续的“1” 作为所在位置的最大宽度maxWeight，那么高度就是在这位置（i, j）基础上上下延伸来枚举，找到符合的最小宽度的那个maxWeight，似乎可行。
使用单调栈进行维护这个maxWeight宽度序列，来找出当前位置上的最小宽度。

// 枚举高度 矩阵的列作为高度
 for(int j = 0; j < n; j++) {
            int[] up = new int[m];
            int[] down = new int[m];

            Deque<Integer> stack = new LinkedList<>();
            for(int i = 0; i < m; i++) {
                while(!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                    stack.pop();
                }
                up[i] = stack.isEmpty() ? -1 : stack.peek();
                stack.push(i);
            }
            stack.clear();
            for(int i = m - 1; i >= 0; i--) {
                while(!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                    stack.pop();
                }
                down[i] = stack.isEmpty() ? m : stack.peek();
                stack.push(i);
            }

最后遍历比较出最大的那个矩阵即可。

力扣题链接：
84 柱状图中最大的矩形
85 最大矩形