插入排序和希尔排序

1. 插入排序

插入排序就是将第k个数插入区间[0,k-1](该区间已经是有序的)中，使之成为一个新的有序区间   [0，k]。

如图

将第一个数作为最开始的区间（必然是有序的），从第2个数开始依次作为k插入前面的区间中

//插入排序
void InsertSort(int* a, int n)
{
	int i = 0;
	for (i = 0; i < n - 1; i++)
	{
		//将第k个数插入[0,k-1]的区间中
		int end = i;  //end作为区间的右端，所以要保证end后面一定还有一个数-->i<n-1
		int tem = a[end + 1];   //  tmp是将要插入的数
		while (end >= 0)
		{
			if (a[end] > tem)  // 大于tmp就后移
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tem;   // 小于tmp 或 end==-1 结束
	}
}

时间复杂度:o(n^2)  空间复杂度o(1)

2. 希尔排序

希尔排序就是再插入排序之前进行预排序，不再是将所有的数作为一组进行排序，选取间距大小为的gap的数作为一组数组进行插入排序，如下图，9 5 8 5作为一组进行排序。

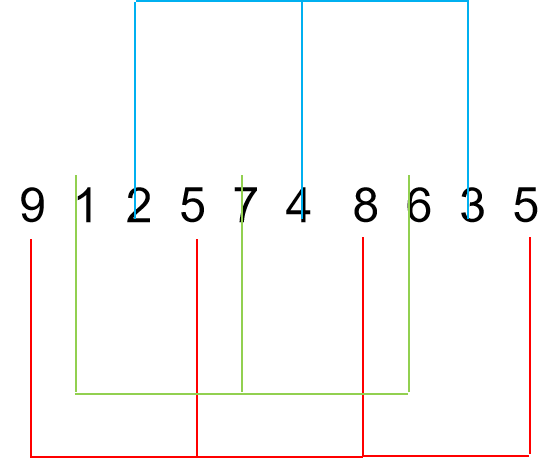
//希尔排序
void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;  //  gap慢慢减小，最后一定等于1
		int end = 0;
		for (int i = 0; i < n  - gap; i++)   
		{
			int k = i + gap;
			int end = i;
			int tmp = a[k];
			while (end >= 0)
			{
				if (a[end] > a[k])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

时间复杂度:nlog(n)<-->n^2      空间复杂度:o(1)