快速排序的思想是找到一个key值(数组中任意的一个数),通过某种排序,将key( a[i] ),移到他本该在的位置,如图。
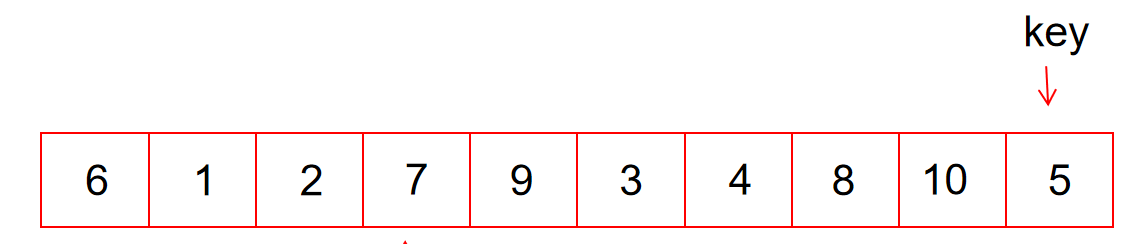

通过排序后,使5的左边都是小于5的数,5的右边都是大于5的数。
再将5作为分割点,对5的左右区间继续相同的排序,直到区间的长度等于1。
递归方式
实现单趟排序
像这样强势的单趟排序有三种
1. 左右指针法
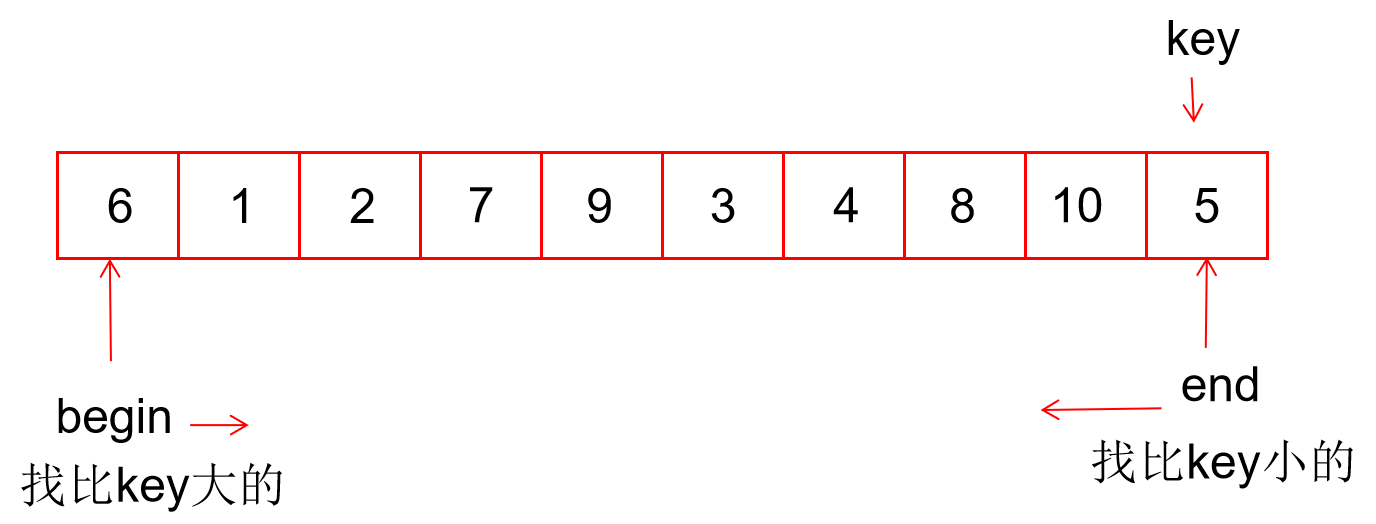
// 左右指针法
int pastsort(int* a, int begin, int end)
{
//三数取中 获取key值
int mid = Getmid(a, begin, end);
int key = a[mid];
// 将key移到末尾
Swap(a[mid], a[end]);
int left = begin;
int right = end;
// 从左边开始找比key大的数,从右边开始找比key小的数,找到了停止,将a[left]和a[rught]交换
while (left < right)
{
while (left < right && a[left] <= key)
{
left++;
}
while (left < right && a[right] >= key)
{
right--;
}
Swap(a[left], a[right]);
}
Swap(a[left], a[end]);
// left==right
// 情况1.left不动,此时a[left]大于key,right移动直到遇到left。
// 情况2.right不动,此时a[right]小于key,a[left]大于key,left和right发生交换,此时a[right]大于于key,left移动直到遇到right。
// left之前都是比key小的数,从key开始都是大于等于key的数,再将a[end]与a[left]交换,使key到排序后的位置
return left; // 返回分割点
}
2. 前后指针法
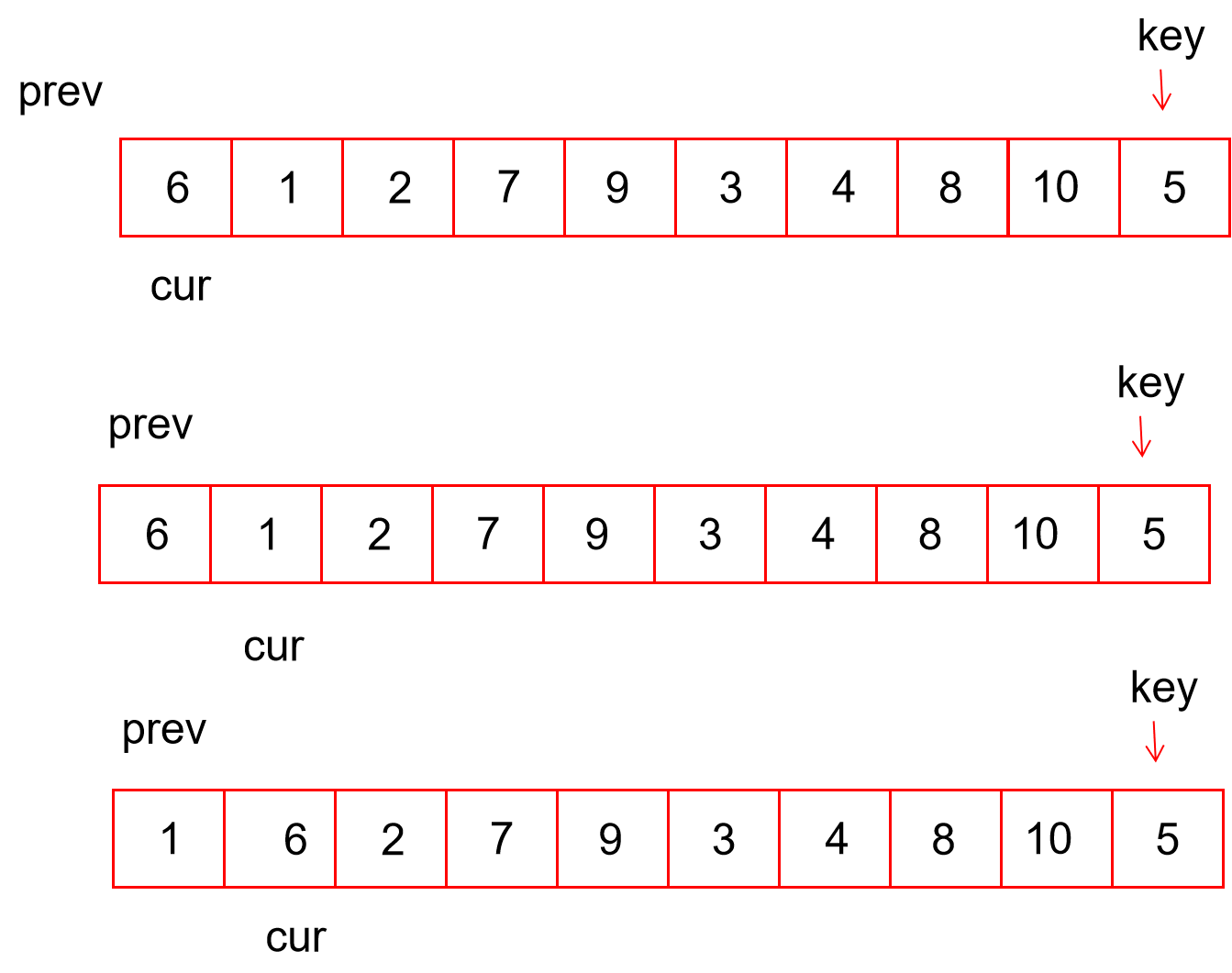
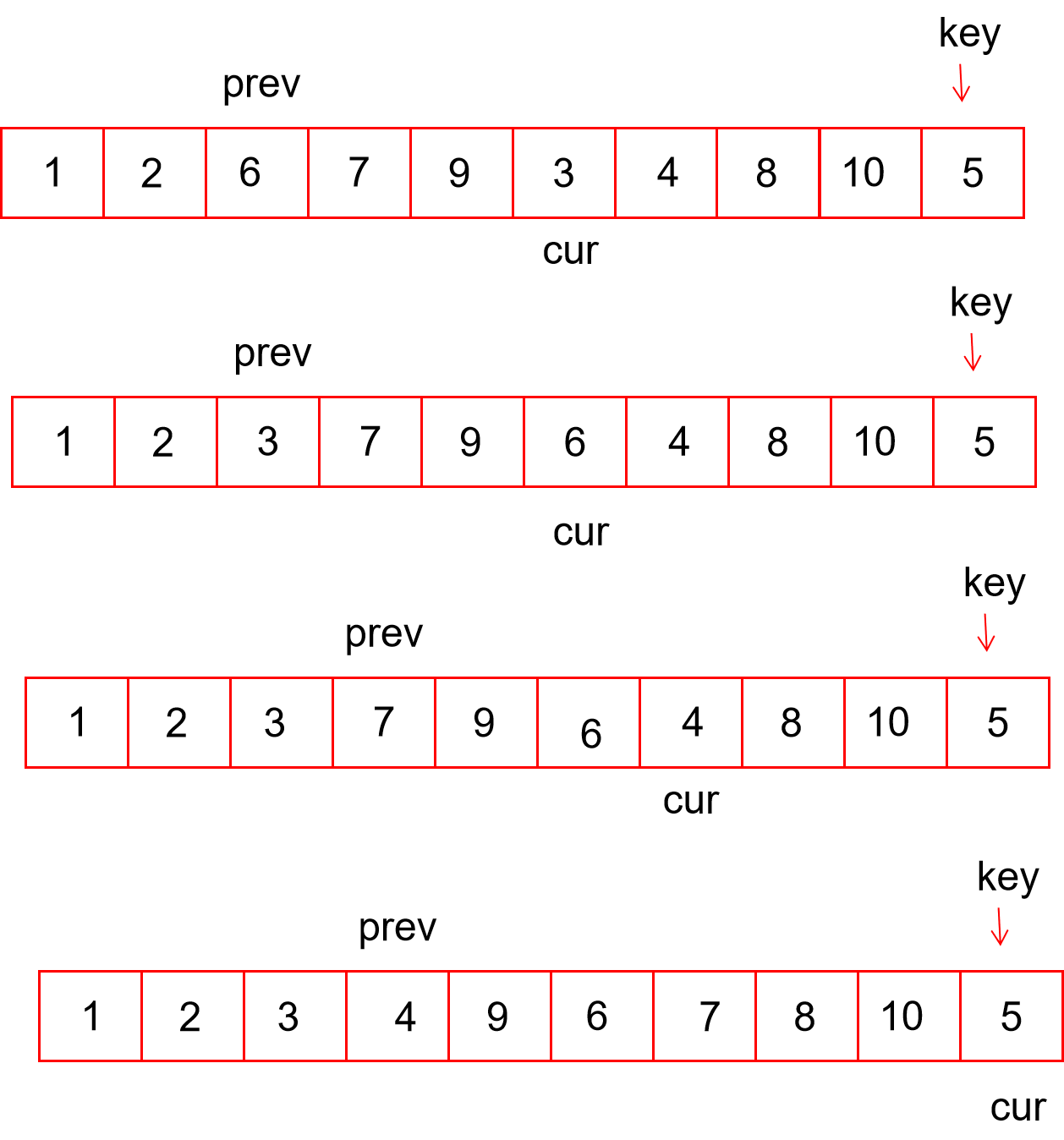
通过两个指针(两个数组下标 prev 和 cur)将小于key的数交换的prev指针之前。
不断cur++如果a[cur]<key,将prev++,交换a[prev]和a[cur] 继续移动cur,prev从-1开始,这样确保了prev每走一步,a[prev]都是小于key的数。
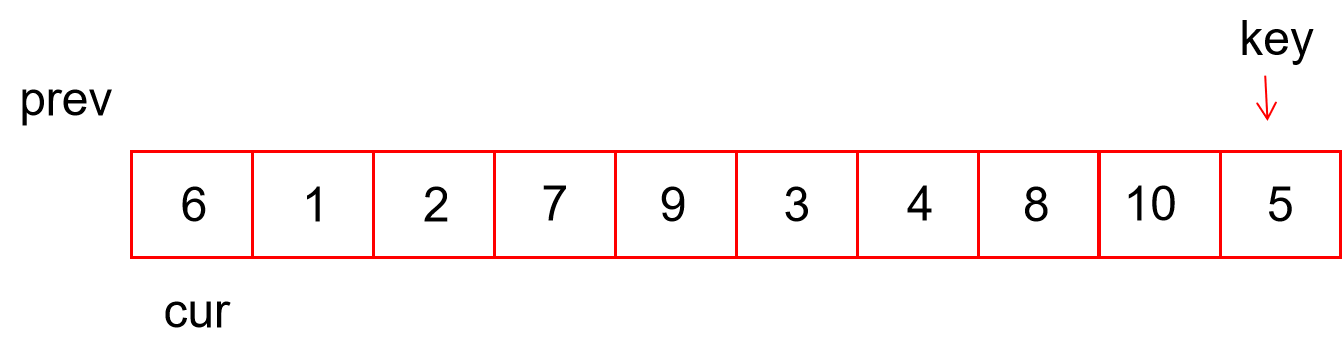
// 前后指针法
int pastsort1(int* a, int begin, int end)
{
int mid = Getmid(a, begin, end);
int key = a[mid];
Swap(a[mid], a[end]);
int prev = begin - 1;
int cur = begin;
while (cur <= end)
{
if (a[cur] < key)
{
prev++;
Swap(a[cur], a[prev]);
}
cur++;
}
// 当cur将全部的数都遍历完了,就是所以小于key的数都在区间[begin,prev]中
prev++;
Swap(a[prev], a[end]); // 将key放在区间的后一个位置
return prev;
}
3. 左右挖坑法
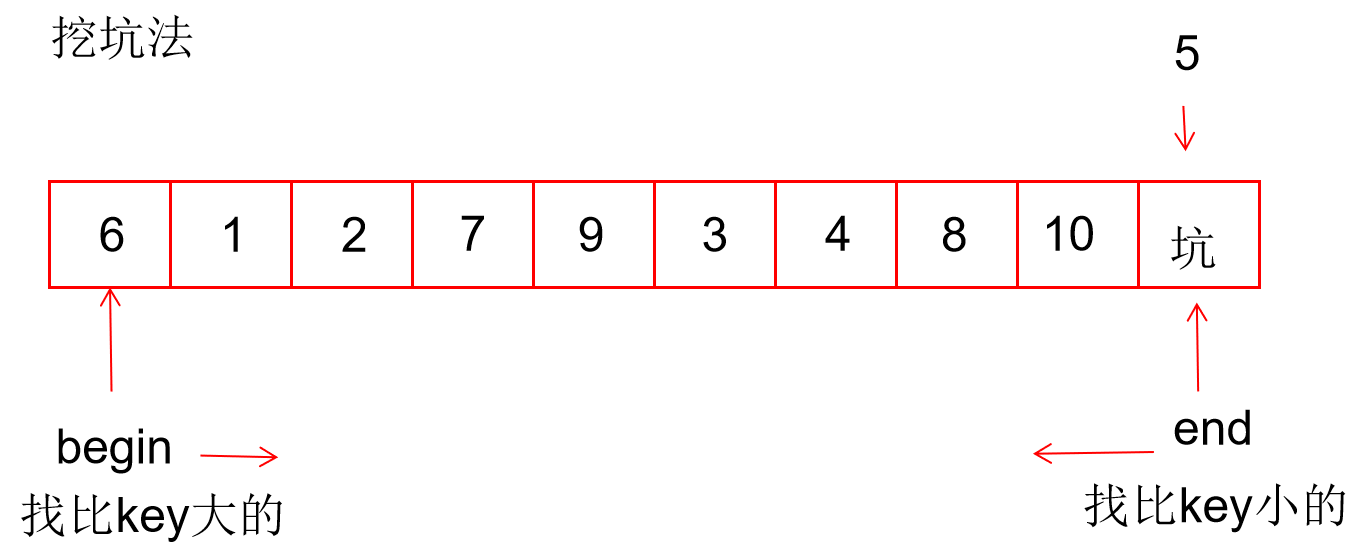

// 左右挖坑法
int pastsort2(int* a, int begin, int end)
{
int mid = Getmid(a, begin, end);
int key = a[mid];
Swap(a[mid], a[end]);
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[left] <= key)
{
left++;
}
Swap(a[left], a[right]);
// 情况1.a[left]>key,用a[left]的数放入a[right]这个坑,并产生新的坑a[left]
// 情况2.left与end相遇,发生自交换
while (left < right && a[right] >= key) // 此时left是坑,从end往前找小于key的数放入坑left中
{
right--;
}
Swap(a[left], a[right]);
}
a[left] = key; // 将key放入left坑中
return left;
}
递归函数
void QuickSort(int* a, int begin,int end) // 指的是数组a的[begin,end]区间
{
if (begin - end >= 0) //长度为1返回
{
return;
}
int div = pastsort2(a, begin, end);
QuickSort(a, begin, div - 1);
QuickSort(a, div + 1, end);
}
// 输出:1 2 4 4 4 5 6 7
为什么要三数取中

当在这种情况下,一直选取end作为key时,我们递归的区间将会是:
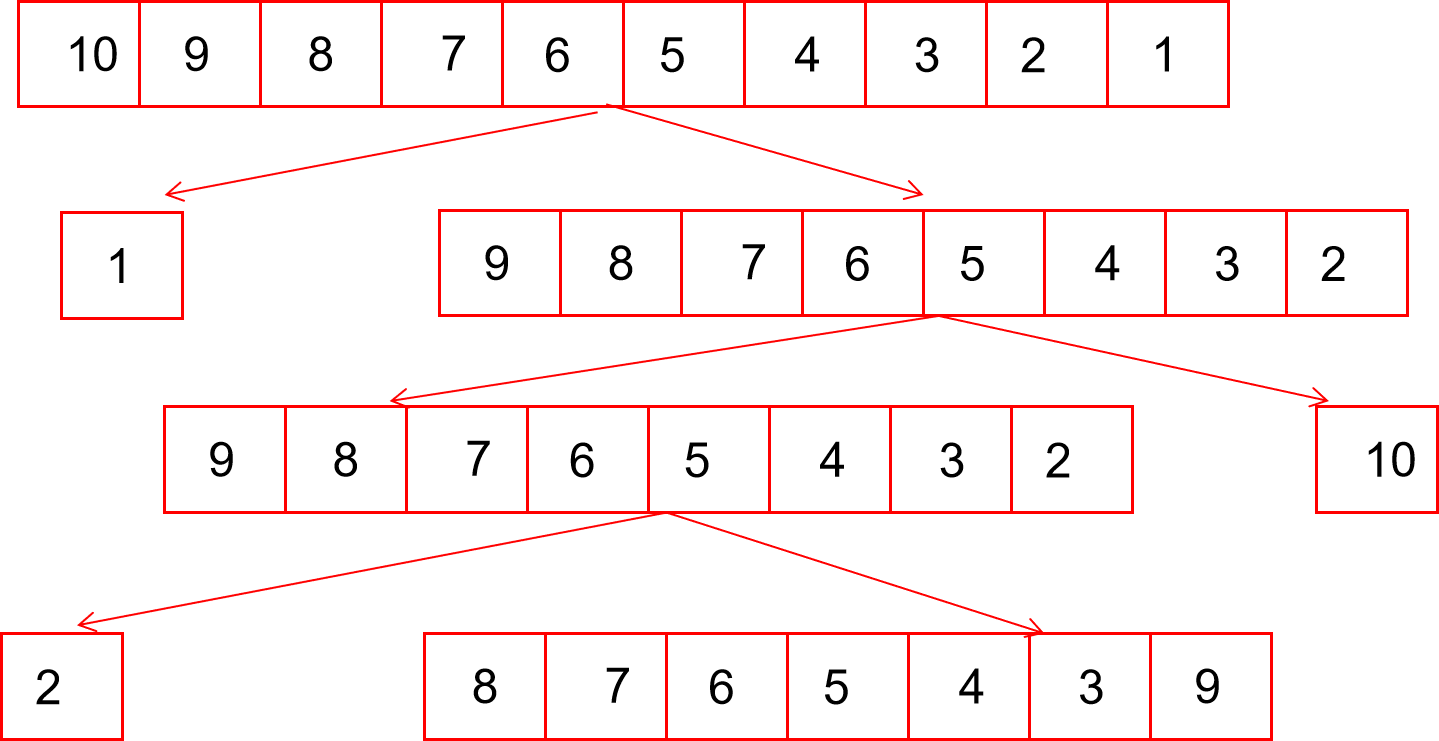
一个数就要递归一个,要递归10次。
当我们用三数取中找key时,我们的递归区间将会是:
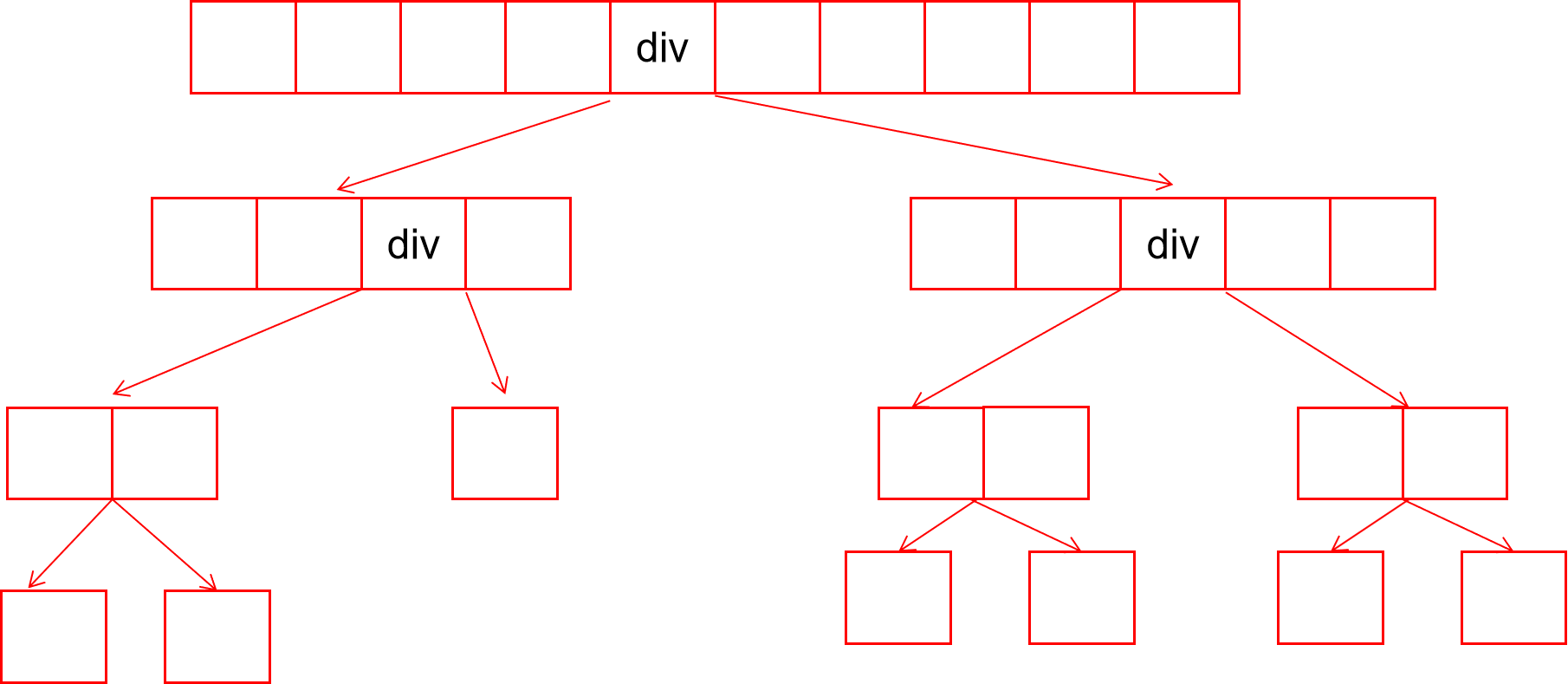
2^(n)=len,一共递归n=log(len)次。
当数组很大的时候,效果相差巨大。
递归太多的危害:
1. 栈溢出
原因:每次递归调用都会在程序的调用栈(Call Stack)中压入一个新的栈帧(存储局部变量、返回地址等)。栈空间有限(通常几MB),递归过深会导致栈耗尽。
表现:程序崩溃,抛出 `StackOverflowError`(如Java)或段错误(如C/C++)。
2.性能问题
时间开销:递归可能重复计算相同子问题(如斐波那契数列的朴素递归解法),时间复杂度指数级增长(如 O(2^n))。
空间开销:栈帧累积占用额外内存,即使算法逻辑正确,也可能因栈空间不足而无法运行。
非递归方式
非递归和递归的单趟排序时一样的,我们要实现主函数。
思路:与递归一样,都要获得区间才能进行单趟排序,在递归下,区间是存放在栈上的。在非递归下,将会把区间放栈堆上面。
先单趟排序获得两个区间

首先实现一个基础的栈
(也可以用C++的头文件#include<stack>)
//自己实现堆栈
class Stack
{public:
int* _arr;
int _size;
int _capacity;
};
void InitStack(Stack **st)
{
*st = new Stack();
(*st)->_capacity = 1;
(*st)->_size = 0;
(*st)->_arr = (int*)malloc(sizeof(int));
}
bool Isfull(Stack* st)
{
// 一次存两个数据
return st->_size + 1 >= st->_capacity;
}
void Addcapacity(Stack* st)
{
st->_capacity *= 2;
int* p = (int*)realloc(st->_arr, sizeof(int) * st->_capacity);
if (p == NULL)
{
return;
}
st->_arr = p;
}
void Push_back(Stack*st ,int begin,int end)
{
if (Isfull(st))
{
Addcapacity(st);
}
// 将区间的下标存入堆栈中
st->_arr[st->_size++] = begin;
st->_arr[st->_size++] = end;
}
void Pop_back(Stack* st)
{
st->_size -= 2;
}
函数框架
void QuickSort1(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
Stack* st = NULL;
InitStack(&st);
int div = pastsort2(a, begin, end); //获得两个区间
Push_back(st, begin, div - 1); //压入栈中
Push_back(st, div + 1, end);
while (st->_size > 0) // 当栈中没有了区间结束(_size==0)
{
int curbegin = st->_arr[st->_size - 2]; // begin是两个数的前一个
int curend = st->_arr[st->_size - 1];
Pop_back(st); // 获取了区间就删除 size-=2;
if (curbegin < curend)
{
div = pastsort2(a, curbegin, curend); //获得两个[curbegin,curend]的子区间
Push_back(st, curbegin, div-1); // 压入栈中 size+=2;
Push_back(st, div + 1, curend);
}
}
}
快速排序的时间复杂度
最好的情况
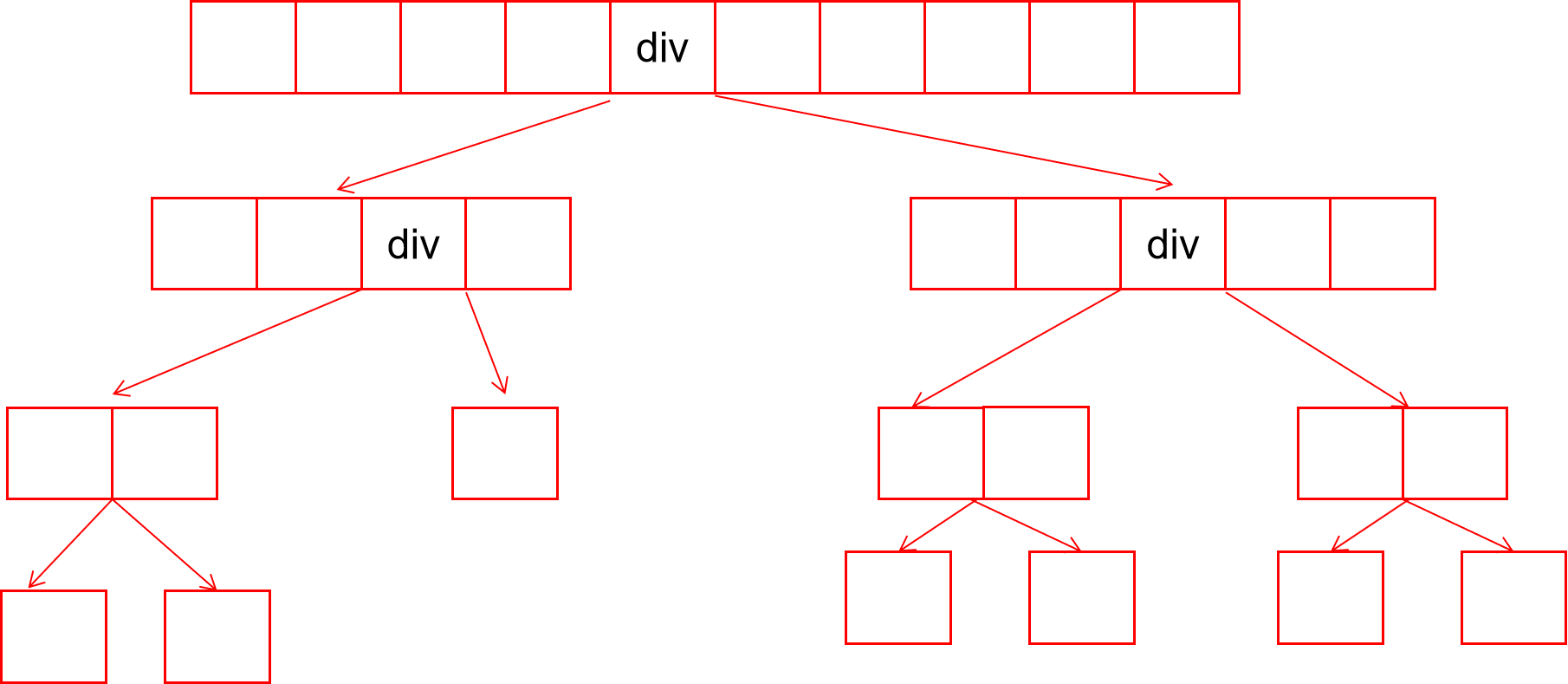
每一次都能将区间分割为左右差不多长度的子区间,令有n个数,设递归的高度为h层
2^(h)=n,h=log(n),每一层都要遍历n个元素,所以时间复杂度为nlog(n)。
最坏情况

时间复杂度为o(n^2)
空间复杂度
最好情况
每一层递归栈空间为o(1),仅存储指针和局部遍历变量,高度为log(n),空间复杂度为o(logn)。
最坏情况
高度为n ,空间复杂度为o(n)。
稳定性
快速排序不稳定,在交换时,相同数值大小的相对顺序可能改变。




















 2529
2529

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








