堆排序
常用性质
- 高度为h的堆,最大元素个数为:(2^(h+1)) -1,最小为(2^h) -1。
- n个元素的堆,高度为log(n)。
- n个元素的堆,叶结点下标是:(n/2),(n/2)+1,……,n-1
- 最小值在叶节点上,最大值就是根节点。
最小堆与之类似。
实现
#include <iostream>
#include <vector>
using namespace std;
#define PARENT(A) (int)(((A)+1)/2) //父节点,A代表下标,由于第一个下标为0,因此这里进行了+1
#define LEFT(A) (int)(2*((A)+1))
#define RIGHT(A) (int)(2*((A)+1)+1)
//使二叉堆从某个节点开始为最大堆
#if 0
//递归方法
void MaxHeapify(vector<int> &heap, int index)
{
if(heap.empty()) return;
int len = heap.size();
int l = LEFT(index); //l为左子树节点在数组中的下标+1
int r = RIGHT(index); //同理
int max_index = 0;
//找到当前节点值、左子树节点值、右子数节点值最大值的下标
if(l <= len && heap[l-1] > heap[index])
max_index = l-1;
else
max_index = index;
if(r <= len && heap[r-1] > heap[max_index])
max_index = r-1;
//不符合最大堆规则的进行交换,并继续判断
if(index != max_index)
{
int tmp = heap[index];
heap[index] = heap[max_index];
heap[max_index] = tmp;
MaxHeapify(heap, max_index);
}
}
#else
//循环,与递归方式类似
void MaxHeapify(vector<int> &heap, int index)
{
if(heap.empty()) return;
int len = heap.size();
int max_index = 0;
while(index < len)
{
int l = LEFT(index);
int r = RIGHT(index);
max_index = index;
if(l <= len && heap[l-1] > heap[index])
max_index = l-1;
if(r <= len && heap[r-1] > heap[max_index])
max_index = r-1;
if(index != max_index)
{
int tmp = heap[index];
heap[index] = heap[max_index];
heap[max_index] = tmp;
}else
{
break;
}
index = max_index;
}
}
#endif
//使整个数组为最大堆,即除了叶结点的所有节点都进行MaxHeapify
void BuildMaxHeap(vector<int> &vec)
{
int len = vec.size();
for(int i = len/2-1; i>=0; --i) //应用性质3,len/2为第一个叶结点
{
MaxHeapify(vec, i);
}
}
//利用最大堆进行排序,最大堆可以确定根节点为最大值,
//每取出一个最大值,用最后一个叶结点代替根节点,
//再执行一次MaxHeapify,又可以保证当前堆为最大堆
//重复这个过程,依次取出最大堆的最大值。
void HeapSort(vector<int> &vec)
{
vector<int> tmp(vec);
BuildMaxHeap(tmp);
int len = tmp.size();
int k = 0;
for(int i = len-1; i > 0; --i)
{
vec[k++] = tmp[0];
tmp[0] = tmp[i];
tmp.pop_back();
MaxHeapify(tmp, 0);
}
vec[len-1] = tmp[0];
}
void DebugPrint(vector<int> &vec)
{
for(int i : vec)
cout << i << " ";
cout << endl;
}
int main()
{
vector<int> heap = {4,16,10,7,14,9,3,2,8,1};
cout << "原数组:" << endl;
DebugPrint(heap);
MaxHeapify(heap,0);
cout << "使第一个节点符合最大堆规则:" << endl;
DebugPrint(heap);
BuildMaxHeap(heap);
cout << "使所有节点符合最大堆规则:" << endl;
DebugPrint(heap);
HeapSort(heap);
cout << "利用最大堆排序:" << endl;
DebugPrint(heap);
return 0;
}
输出结果
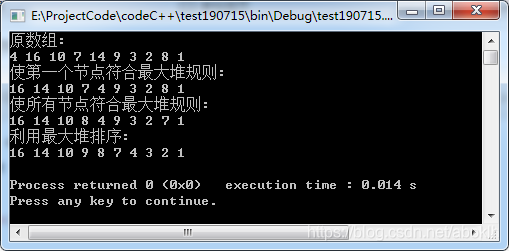








 本文介绍了堆排序的基本性质,包括最大堆和最小堆的特点。堆排序的高度与元素数量的关系被详细阐述,指出n个元素的堆高度为log(n)。文章还提及堆排序的实现过程,并给出了操作后的输出结果。
本文介绍了堆排序的基本性质,包括最大堆和最小堆的特点。堆排序的高度与元素数量的关系被详细阐述,指出n个元素的堆高度为log(n)。文章还提及堆排序的实现过程,并给出了操作后的输出结果。
















 686
686

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








