布隆过滤器的一些总结理解

应用背景：

在内容中，查找某个单词是否存在

网络爬虫url程序，判断去爬的url是否访问过

垃圾邮件（短信）过滤算法设计

公共安全，判断嫌疑人是否在网逃名单中

以上的应用背景都是在很多数据中，判断是否存在其中

需求：

在海量数据中查询某条信息是否在

解决思路：

c++ 中常见stl容器结构set和map结构，都是采用红黑树实现方式，增删改查的时间复杂度o(log⑵N)

红黑树是可以存储相同key可以信息，map存储key和value信息，set只存储key信息不可重复

优势：存储效率高，访问速度快

缺陷：对于数据量较大查询字符串比较长，当查询字符串是都需要进行匹配判断，速度会减慢

c++ stl结构 unordered_map<string,bool>采用hashtable实现，由数组+hash函数构成

将字符串通过hash函数生成整数，再映射到数组中，增删改查时间复杂度o(1);

在字符串通过hash函数生成整数是，会有冲突情况，常见解决方案如下：

链式法：

引入链表来处理哈希冲突，将冲突元素用链表链接起来；

这会出现一种极端情况，冲突元素过多，该冲突链表过长，这个时候可以将这个链表转换成红黑树，原来链表时间复杂度o(n)转换成红黑树时间复杂度o(log⑵N), 什么时候判断链表过长？

采用256个节点 经验值，进行转换

开放寻址法：

将所有元素都存放到哈希表中，一般使用线性探查思路解决

 1.当插入新元素，通过哈希函数在哈希表中定位

 2.检查数组中这个槽位是否存在元素，如果为空，则存储到这个位置中

 3.如果在2中不为空，索引加上一定步进补偿，继续检查2步骤

这两种哈希方式，会导致hash聚集，即近似值都聚集在一起；

以上方式改进可以使用双重哈希，解决hash聚集现象，但是存储效率不高，需要更大的空间换时间

总结：红黑树和hashtable都不是太好的解决海量数据问题，都需要存储具体字符串；

如果数据量大，内存空间不需要很大，就需要探寻不存储key方法，并且拥有hashtable优点的存储方式呢？

布隆过滤器

定义：是一种概率型数据结构，它的特点提供了高效的插入和查询，能明确告知某个字符串一定不存在或者可能存在的解决方式了

优势和劣势：比传统查询结构（hash，set，map等数据结构）更加高效，占用空间更小；但是其缺点是返回结果是概率性的，结果会存在误差，这个误差是可控的，不足地方还有就是不支持删除操作

组成：有位（bit数组）+n个hash函数

原理：当一个元素加入位图中，通过n个hash函数将这个元素映射到位图中n个带点，并把这个位置置位1,；当检索查询是，再通过k个hash函数运算检测位图中k个点是否都是1；如果有部位1的点，那么认定这个元素不存在；如果全为1，则该元素可能存在（存在误差）

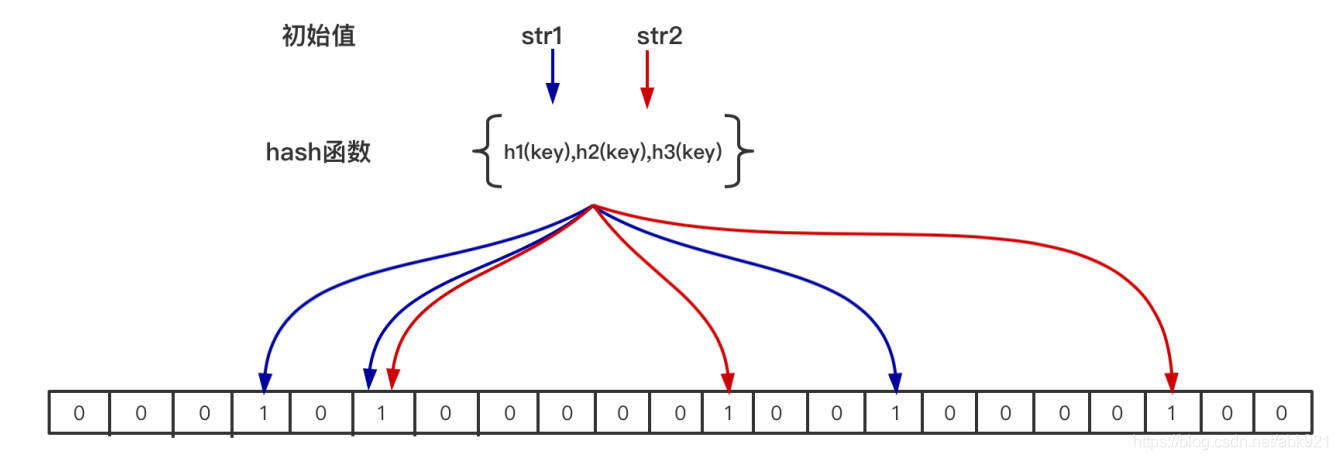
在位图中每个槽位只有0或1状态，一个槽位被设置为1状态，但是不明确它被设置了多少次，

也是不知被多个str1哈希映射以及是被那个hash函数映射过来的；所以不支持删除操作

在实际应用过程中，布隆过滤器如何使用呢？需要选择多少个hash函数，需要分配多少空间的位图，存储多少元素？如何控制假阳率（能明确一定不存在，不能明确一定存在，存在的判断是有误差的，假阳率是错误判断存在的概率）

n  布隆过滤器元素个数，上图 str1和str2 两个元素 n=2;

p  假阳率，在0-1之间， 0.000000

m  位图所占空间

k   hash函数的个数

公式如下：

n = ceil(m / (-k / log(1 - exp(log(p) / k))))

p = pow(1 - exp(-k / (m / n)), k)

m = ceil((n * log(p)) / log(1 / pow(2, log(2))));

k = round((m / n) * log(2));

 

假定选取这四个值：

 

n = 4000

p = 0.000000001

m = 172532

k = 30

 

四个值的关系：

 

 

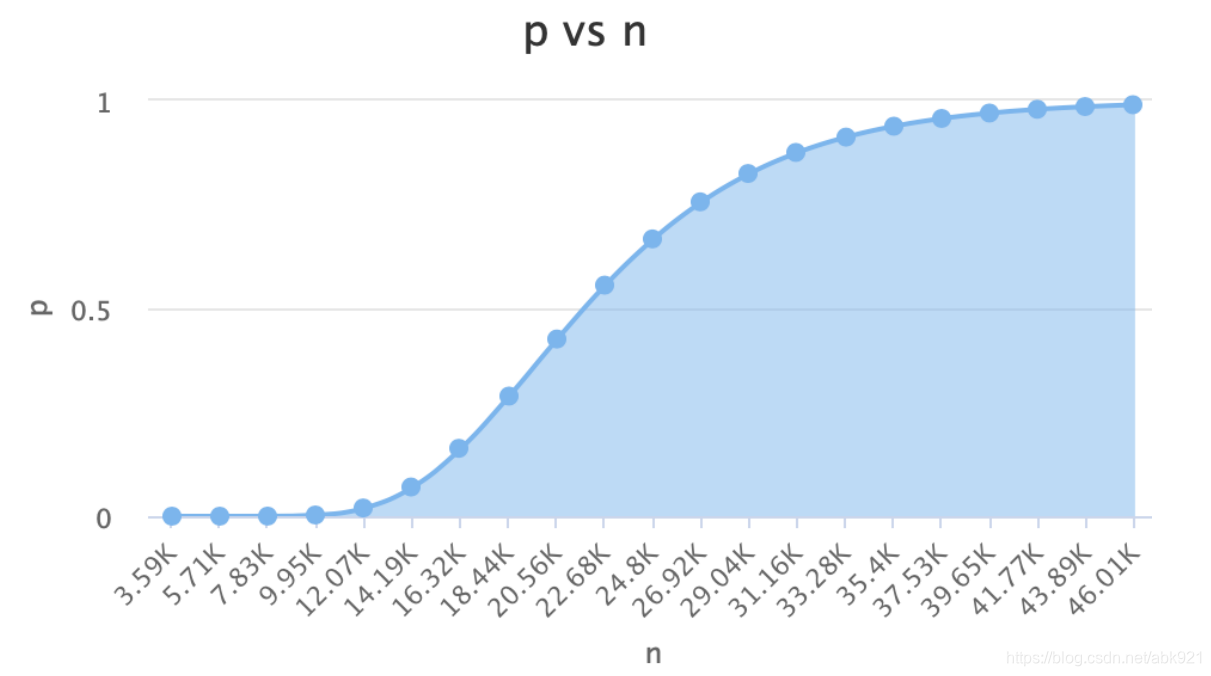
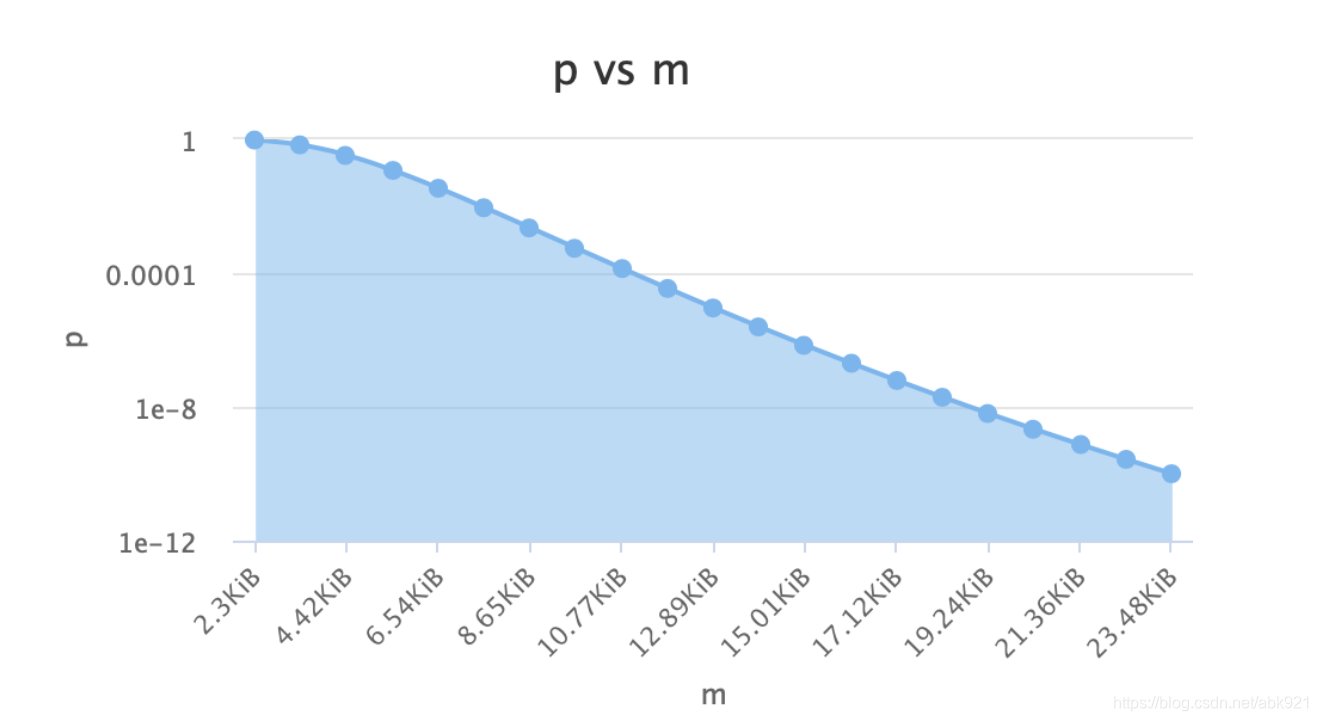
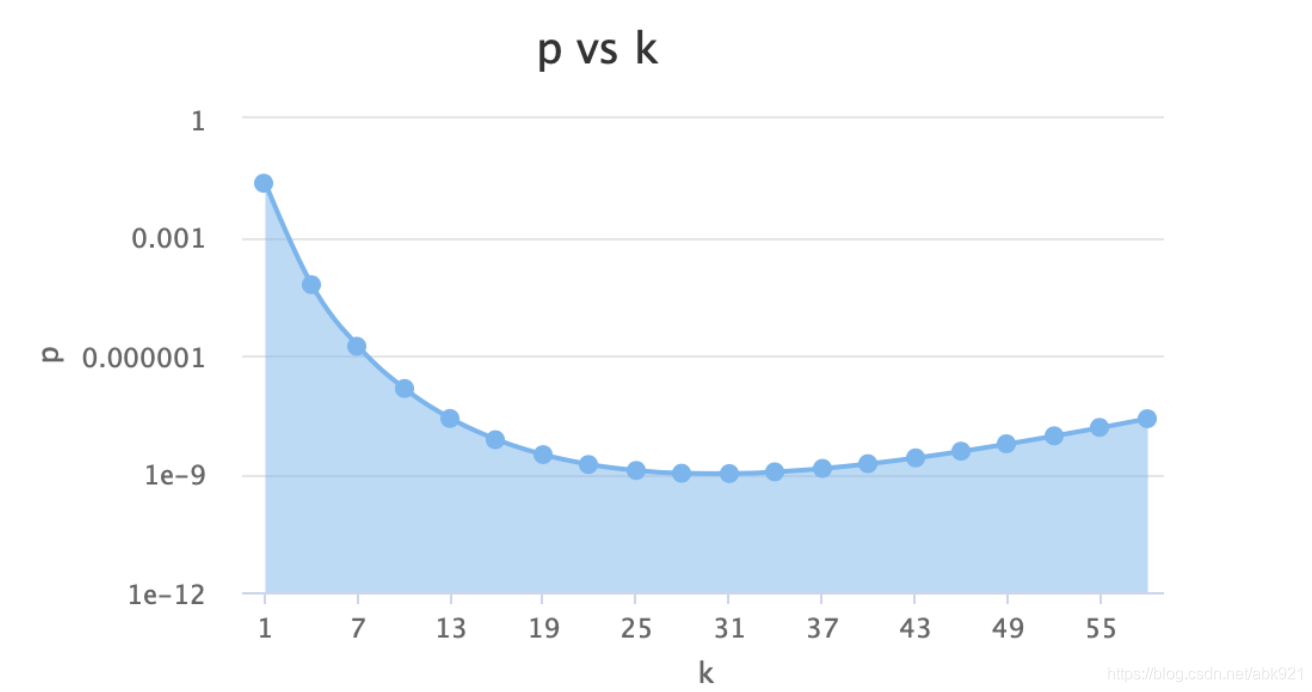
在实际应用中，我们可以确定n和p,通过上面的计算算出m和k；

已知k，如何选择k个hash函数？

 

// 采⽤⼀个hash函数，给hash传不同的种⼦偏移值
// #define MIX_UINT64(v) ((uint32_t)((v>>32)^(v)))
uint64_t hash1 = MurmurHash2_x64(key, len, Seed);
uint64_t hash2 = MurmurHash2_x64(key, len, MIX_UINT64(hash1));
for (i = 0; i < k; i++) // k 是hash函数的个数
{
    Pos[i] = (hash1 + i*hash2) % m; // m 是位图的⼤⼩
}
// 通过这种⽅式来模拟 k 个hash函数 跟我们前⾯开放寻址法 双重hash是⼀样的思路