二叉树、树、森林之间的转换

一、背景

树、森林与二叉树之间有一个自然的对应关系，它们之间可以互相转换，即任何一个森林或一棵树都可以唯一地对应一棵二叉树，而任一棵二叉树也能唯一地对应到一个森林或一棵树上。正是由于有这样的一一对应关系，可以把在树中处理的问题对应到二叉树中进行处理，从而把问题简单化，因此二叉树在树的应用中显得特别重要。

二、树转换为二叉树

将一棵树转换为二叉树的过程如下：

• 树中所有相邻兄弟之间加一条连线；
• 对树中的每个结点只保留它与左数第一个孩子之间的连线，删除与其他孩子之间的连线；
• 以树的根结点为轴心，将整棵树顺时针转动 45°，使之结构层次分明。
  上述过程中，每个结点左指针指向该此结点的第一个孩子，右指针指向它在树中的相邻右兄弟，即“左孩子右兄弟”规则。根结点没有兄弟，故对应的二叉树没有右子树。
  例题 1： 将图 1(a) 中的树转换为二叉树。其转换过程如图 1(b)~(d) 所示。
  

三、森林转换为二叉树

森林是由两棵或两棵以上的树构成的，将森林转换为二叉树的过程如下：

• 将森林中的每棵树转换成相应的二叉树。
• 第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子结点，当所有二叉树连在一起后，即得到的二叉树就是森林转换得到的二叉树。
  例题 2：将图 2(a) 所示的森林转换为二叉树。其过程如图 2(b)~(e) 所示。
  
  例题 3：设森林 F 中有 3 棵树，第 1、2、3 棵树的结点个数分别为 9,8,7。将 F 转换为二叉树，该二叉树根结点的右子树上的结点个数是多少？
  解答：与森林 F 对应的二叉树根结点的右子树上的结点，是由第 2 和第 3 棵树的全部结点转换而来的，所以二叉树根结点的右子树上的结点个数是：8+7=15。

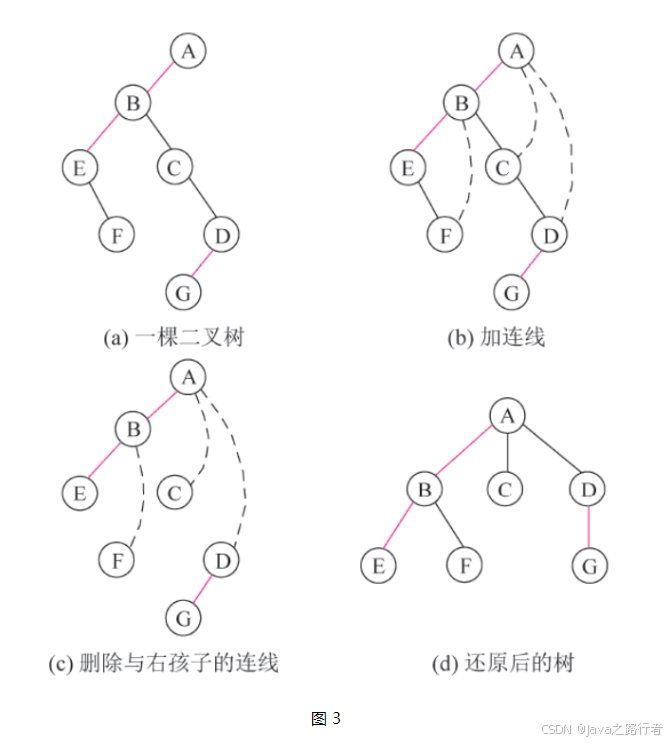
四、二叉树还原为树

基本方法是：将二叉树中的左分支保持不变，右分支还原成兄弟关系。具体过程如下：

• 若某结点是双亲的左孩子，则把该结点的右孩子、右孩子的右孩子等都与该结点的双亲结点用连线连接起来。
• 删除原二叉树中所有双亲结点与右孩子结点之间的连线。
• 整理由前面所得到的树，即以根结点为轴心，逆时针转动 45°，使之结构层次分明。
  例题 4：将图 3(a) 中的一棵二叉树还原为一棵树。还原过程如图 3(b)~(d) 所示。
  

五、二叉树还原为森林

若一棵二叉树是由 棵树构成的森林转换而来的，该二叉树的根结点一定有 个右孩子，该二叉树还原为森林的过程：

• 抹掉二叉树根结点右链上的所有结点之间的“双亲—右孩子”关系，将其分成若干个以右链上的结点为根结点的二叉树，设这些二叉树为
• 分别将上述二叉树各自还原成一棵树。
  例题 5： 将图 4(a) 所是的二叉树还原为森林。还原过程如图 4(b) 和 4© 所示。