离散傅立叶变换 - 简单理解

前言

网络、书籍上有很多关于傅立叶变换的知识，屌丝总有一种感觉：知道这玩意名字N年了，但就是不知道它是啥玩意。

FFT参考资料

频域图像滤波(https://blog.youkuaiyun.com/on2way/article/details/46981825)

目的

可用。

关键点

1. 只需要掌握dft，其他傅立叶变换在程序里是无法实现的。

2. 时域与空域

When you see the term "time domain" in Fourier analysis, it may actually refer to samples taken over time, or it might be a general reference to any discrete signal that isbeing decomposed.

3. Base Function

假设空域是1x32的图像，其可由以下16+1个频率的正弦、余弦基础函数c0~c16、s0~s16构成。理论上有更高频率如c17、c18....，但c16、s16已达到离散数据可表达的最大频率，这也是FFT后图像对称的原因。其中，由FFT计算公式(可参见以下opencv示例)可知，c0计算得到的实数部分幅值为整幅图像的灰度均值，s0对应的虚部幅值则为0。

    

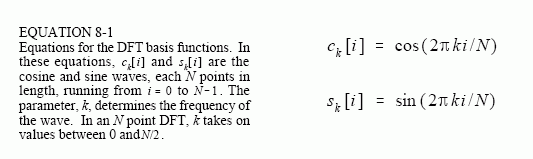
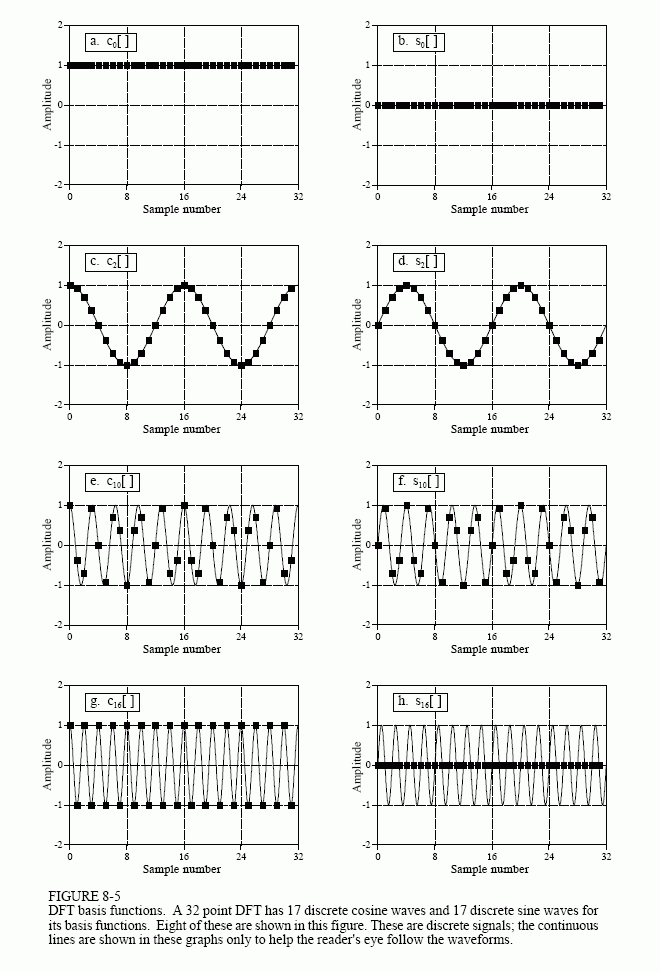
4. 实数部分-cos  虚数部分-sin

The names real part and imaginary part originate from the complex DFT, where they are used to distinguish between real and imaginarynumbers. Nothing so complicated is required for the real DFT. Until you get to Chapter 29, simply think that "real part" means the cosine wave amplitudes, while "imaginary part" means the sine wave amplitudes. Don't let these suggestive names mislead you; everything here uses ordinary numbers.

5.opencv里的幅值

Rectangular and polar notation allow you to think of the DFT in two different ways. With rectangular notation, the DFT decomposes an Npoint signal into N/2 + 1 cosine waves and N/2 + 1 sine waves, each with a specified amplitude. In polar notation, the DFT decomposes anN point signal into N/2 + 1 cosine waves, each with a specified amplitude (called the magnitude) and phase shift. 

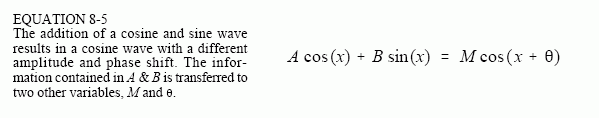
opencv计算DFT的例子，是polar notation的方式，例子中倾斜方向频率(u,v)的magnitude比其他频率高。

备注：实数dft的虚部符号i仅是为了对齐复数dft计算，实际理解可以把其去掉

6.dft计算(http://www.dspguide.com/ch8/6.htm)

复数极坐标表示：http://mengqi92.github.io/2015/10/06/complex/

dft/idft公式：https://snowztail.com/index.php/2017/11/20/dft-2/

DFT物理意义的简单理解

一副图像可由不同频率的正弦、余弦波形(rectangular notation)构成，即可由不同频率的余弦波(polar notation)构成

Demo

http://bigwww.epfl.ch/demo/basisfft/demo.html

其他

维纳滤波：python(https://blog.youkuaiyun.com/bingbingxie1/article/details/79398601)  matlab(https://www.mathworks.com/help/images/image-deblurring.html#bqqhk6c) opencv(https://docs.opencv.org/trunk/de/d3c/tutorial_out_of_focus_deblur_filter.html)