BZOJ 3884 上帝与集合的正确使用方法

扩展欧拉定理

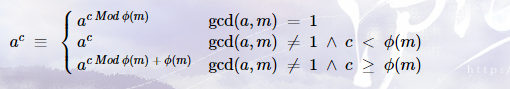
当\(gcd(a,m)=1\)时就是欧拉定理

后面两种情况对\(gcd\)无要求，注意\(c\)与\(\phi(m)\)的关系

\(Description\)

求\(2^{2^{2^{2^{\cdots}}}}(mod　p)\)
简化为求\(x\equiv 2^x　(mod 　p))\)

\(Solution\)

因为\(2^{2^{2^{2^{\cdots}}}} > \phi (p)\)
且\(\phi(p)\)在不断缩小，所以用第三个公式即可
用\(ans(p)\)表示对\(p\)取模的答案，显然\(ans(p)=2^{ans(\phi(p))+\phi(p)}\)
\(\phi(p)\)在不断缩小，直到为\(1\)时，则任何数\(mod　1=0\)，所以到达递归边界，返回\(0\)即可

\(Code\)

#include <cstdio>
#define int long long

typedef long long ll;
const int N = 1e7+71;

int p_(ll x, int y, int z) {
    int ret = 1;
    for (; y; (x *= x) %= z, y >>= 1) if (y & 1) (ret *= x) %= z;
    return ret;
}
signed phi[N];
ll solve(int p) {
    if (p == 1) return 0;
    return p_(2, solve(phi[p]) + phi[p], p);
}
int t, p;

signed main() {
    phi[1] = 1;
    for (signed i = 2; i < N; i++) if (!phi[i]) {
        for (signed j = i; j < N; j += i) {
            if (!phi[j]) phi[j] = j;
            phi[j] = phi[j] / i * (i-1);
        }
    }
    for (scanf("%lld", &t); t--; ) {
        scanf("%lld", &p);
        printf("%lld\n", solve(p));
    }
}

转载于:https://www.cnblogs.com/Liuz8848/p/11371548.html