决策树

决策树（Decision Tree）是一种基本的分类和回归的方法。决策树模型呈现树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。相比朴素贝叶斯分类，决策树的优势在于构造过程中不需要任何领域知识或参数设置。

A、决策树定义：

决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部节点和叶节点，内部节点表示一个特征或属性，叶节点表示一个类。一个决策一般终止于叶节点。

B、决策树分类过程：

从根节点开始，对实例的某一个特征进行测试，根据测试结果，将实例分配到其子结点；此时，每一个子节点对应着该特征的一个取值。如此递归向下移动，直至达到叶节点，最后将实例分配到叶节点的类中。

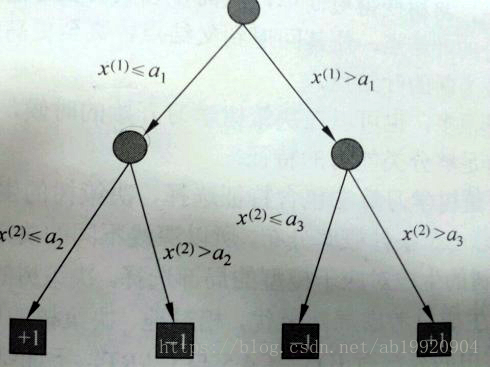
如图所示，由根节点开始，选择某一实例的x(1)属性大于还是小于a1，然后再选择这里实例的x(2)属性满足的条件，如此继续下去，到达叶节点，得到分类为+1或-1。由此看来，决策树还表示给定属性（或特征）条件下类的条件概率分布。

C、决策树的学习

决策树学习算法包含特征选择，决策树的生成和剪枝过程。决策树的学习算法通常是递归地选择最优特征，并用最优特征对数据集进行分割。开始时，构建根节点，选择最优特征，该特征有几种值就分割为几个子集，每一个子集分别递归调用此方法，返回结点，返回的结点就是上一层的子节点。直到所有特征都已经用完，或者数据集只有一维特征为止。

D、特征选择

特征选择问题是希望选取对训练数据具有良好分类能力的特征，这样可以提高决策树学习的效率。

（1）、熵（entropy）--->表示随机变量不确定的度量。熵越大，随机变量的不确定性就越大。

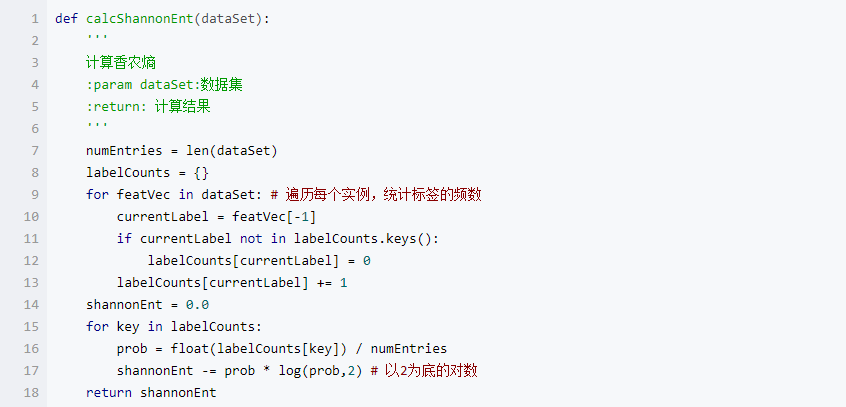
（2）、条件熵（conditional entropy）--->H(Y/X)表示在已知随机变量X的条件下随机变量Y的不确定性

（3）、信息增益（information gain）--->表示得知特征X的信息而使得类Y的信息的不确定性减少的程度.特征A对训练数据集D的信息增益g（D，A），定义为集合D的经验熵H（D）与特征A给定条件下D的经验条件熵H（D/A）之差，即

g（D,A）=H（D）-H(D/A)

这个差又称为互信息。信息增益大的特征具有更强的分类能力。

根据信息增益准则的特征选择方法是：对训练数据集（或子集）计算其每个特征的信息增益，选择信息增益最大的特征。 

输入：训练数据集D和特征A；输出：特征A对训练数据集D的信息增益g（D,A）

(1)计算数据集D的经验熵H（D）;(2)计算特征A对数据集D的经验条件熵H（D/A）;(3)计算信息增益  g（D,A）=H(D)-H(D/A)

4、信息增益比（information gain ratio）

特征A对训练数据集D的信息增益比gR（D,A）的定义为其信息增益g（D,A）与训练数据集D关于特征A的值得熵HA(D)之比，即

gR（D,A）=g（D,A）/HA（D）

E、决策树的生成

主要介绍决策树学习的生成算法：ID3和C4.5

1、ID3算法

2、C4.5算法

文章链接：https://blog.youkuaiyun.com/HerosOfEarth/article/details/52347820