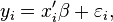
yi称为应变量
xi称为自变量
beta称为参数向量; beta的长度为p. 样本数为n, n>p
epilson称为随机误差
对所有评价函数有两个假设:
1 矩阵X的秩为p. X 线性无关、满秩
2 xi不包含误差因素, error-free。 误差提到了epilson中
经典线性无关模型:
1 epilson期望为0
2 方差为 d, 服从正态分布
OLS, ordinary least squares
假设b就是参数beta的取值, yi - xi * b称为第i项观测的 residual残差。
SSR, sum of squared residual 称为残差平方和S(b)
S(b) = sigma(yi - xi * b)^2 = (y - Xb)' * (y - Xb)
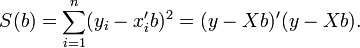
b使得S(b)取值最小, 称为OLS estimator for beta。
beta = min(b|S(b)) = (X'X)-1X'y

After we have estimated β, the fitted values (or predicted values) from the regression will be
y = X*beta = P y






















 3142
3142

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








