小易喜欢的数列

原创已于 2025-05-03 18:38:29 修改 · 356 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2025-05-03 18:19:40 首次发布

题目：

小易喜欢的数列有以下性质的数列

（1）数列的长度为n。

（2）数列中的每个数都在1到k之间（包括1和k）。

（3）对于位置相邻的两个数A和B（A在B前），都满足A<=B或A MOD B != 0（满足其一即可）。

例如，n=4，k=7，那么{1，7，7，2}，它的长度是4，所有数字也在1到7的范围内，并且满足性质（3），所以小易是喜欢这个数列的。但是小易不喜欢{4，4，4，2}这个数列。小易给出n和k，希望你能帮他求出有多少个是他喜欢的数列。

输入格式：
输入包括两个整数n和k（1<=n<=10,1<=k<=10000）。

输出格式：
输出一个整数，即满足要求的数列个数，因为答案可能很大，输出对1 000 000 007取模的结果。

1）问题分析

这个问题要求计算满足特定条件的数列数量，其中数列长度为n，每个元素都在1到k之间。关键是理解并处理相邻元素之间的约束条件。

2）算法设计

先定义 dp[i][j] 用于表示长度为i且最后一个元素为j的数列的可能数目。
对长度为1的数列，每个可能的元素（1到k）都是有效的，所以初始状态dp[1][j] = 1。
对长度为i的数列，其最后一个元素为j时，可以通过遍历所有可能的前一个元素x（1到k），并检查 x 和 j 是否满足条件，累加所有可能的前缀组合数。
最后，所有可能的数列的数目是所有dp[n][j]的总和，其中j从1到k。

3）伪代码

算法：计算满足条件的数列个数
输入：整数n和k
输出：满足条件的数列个数（mod 10^9+7）

1. 初始化 dp[1...k] 为 1 // 长度为1时，每种数列有且仅有一个
2. 对于 i = 2 到 n:
2.1 初始化 new_dp[1...k] 为 0
2.2 对于 j = 1 到 k:
2.2.1 对于 x = 1 到 k:
2.2.2 如果 x ≤ j 或者 x % j ≠ 0:
2.2.3 new_dp[j] += dp[x]
2.2.4 new_dp[j] %= MOD
2.3 dp = new_dp // 更新dp数组
3. 计算总和 sum(dp[1...k])
4. 返回 sum

4）算法思维导图

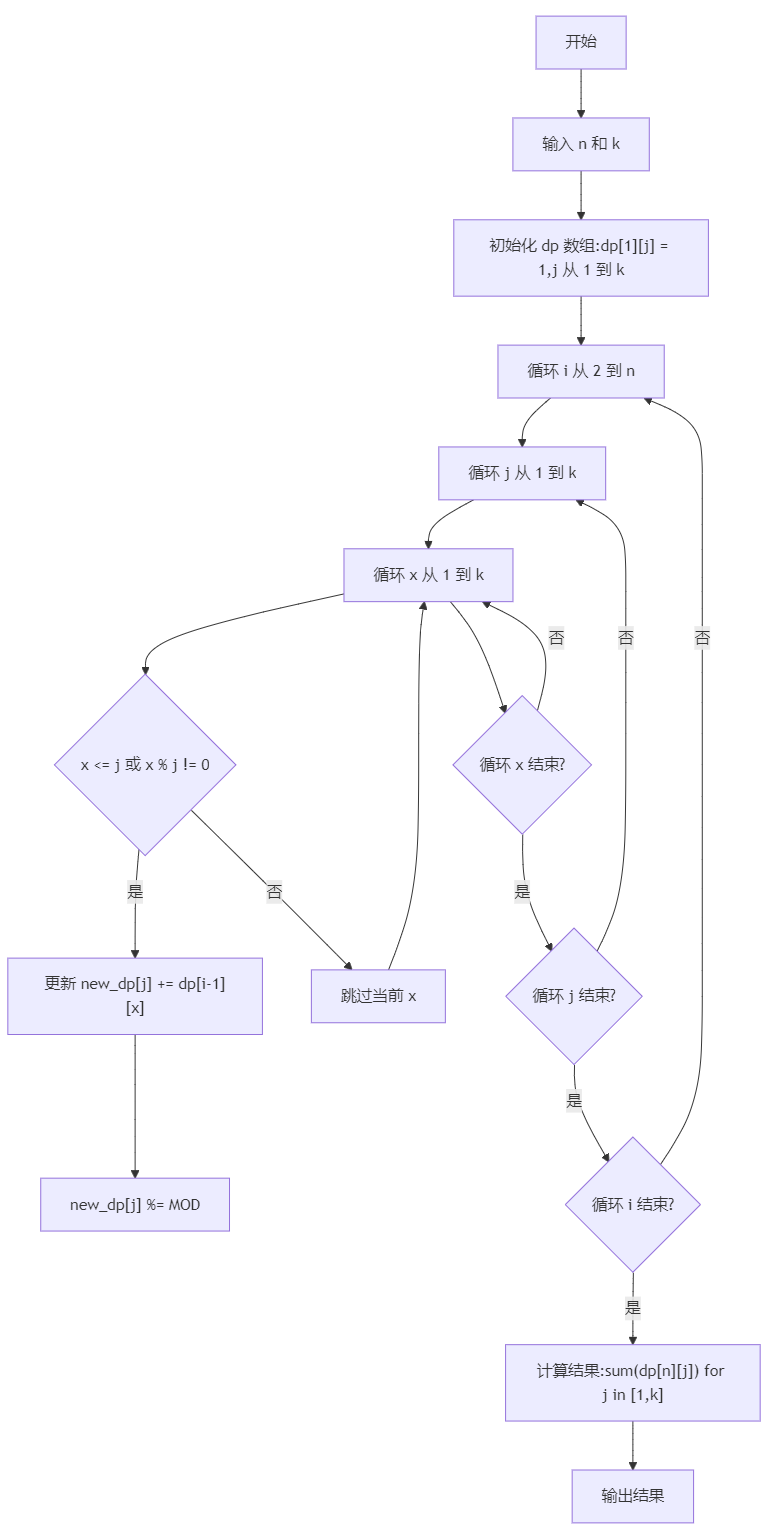
5）算法时间复杂度分析

外层循环n次,中层循环n次，内层循环n次，且每次操作都是常数时间。因此，时间复杂度为O(n3)

6）输出结果

7）实验心得

通过这次实验，我深刻理解了动态规划在组合计数问题中的应用。本题的关键在于正确地定义状态以及状态转移方程，并且需要注意模运算的时机以避免溢出。这道题也让我认识到在面对大数据规模时算法效率的重要性。虽然本题的直接动态规划解法在给定的约束下是可行的，但它提示我们在遇到类似问题时应该思考是否有更优的解决方案。

8) 完整代码

#include <stdio.h>
#include <string.h>

#define MOD 1000000007

int dp[11][10001];

int isValid(int A, int B) {
    return A <= B || A % B != 0;
}

int main() {
    int n, k;
    scanf("%d %d", &n, &k);

    memset(dp, 0, sizeof(dp));
    for (int j = 1; j <= k; j++) {
        dp[1][j] = 1;
    }

    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= k; j++) {
            for (int x = 1; x <= k; x++) {
                if (isValid(x, j)) {
                    dp[i][j] = (dp[i][j] + dp[i - 1][x]) % MOD;
                }
            }
        }
    }

    int result = 0;
    for (int j = 1; j <= k; j++) {
        result = (result + dp[n][j]) % MOD;
    }

    printf("%d\n", result);
    return 0;
}