葫芦书笔记----概率图模型

概率图模型

概率图模型的联合概率分布

能否写出图中贝叶斯网络的联合概率分布？

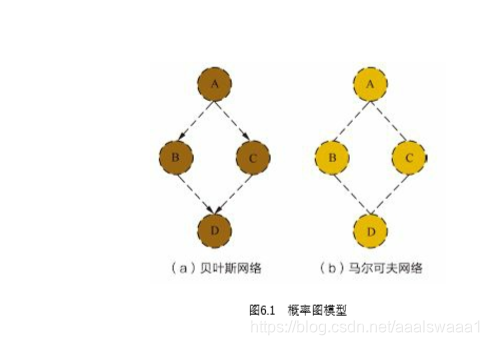
可见，在给定A的条件下B和C是条件独立的，基于条件概率的定义可得
$$P(C|A,B)=\frac{P(B,C|A)}{P(B|A)}=\frac{P(B|A)P(C|A)}{P(B|A)}$$
同理，在给定B和C的条件下A和D是条件独立的，可得
$$P(D|A,B,C)=\frac{P(A,D|B,C)}{P(A|B,C)}=\frac{P(A|B,C)P(D|B,C)}{P(A|B,C)}$$
由式1，2可得联合概率
$$P(A,B,C,D)=P(A)P(B|A)P(C|A,B)P(D|A,B,C)=P(A)P(B|A)P(C|A)P(D|B,C)$$

###能否写出图中马尔可夫网络的联合概率分布

在马尔可夫网络中，联合概率分布的定义为
$$P(x)=\frac{1}{Z}\prod _{Q\in C}{\phi }_Q(x_Q)$$
具体的看书。

概率图表示

看书

生成式模型与判别式模型

###生成式模型与判别式模型的区别是什么？

速记：假设可观测到的变量集合为X，余姚预测的变量集合为Y，其他的变量集合为Z。

生成式模型：对联合概率分布P（X，Y，Z）进行建模，在给定观测集合X的条件下，通过计算边缘分布来得到对变量集合Y的推断，即
$$P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{{\sum }_{Z}P(X,Y,Z)}{{\sum }_{Y,Z}P(X,Y,Z)}$$
判别式模型：直接对条件概率分布P（Y，Z|X）进行建模，然后消掉无关变量Z就可以得到对遍历集合Y的预测，即
$$P(Y|X)=\sum _{Z}P(Y,Z|X)$$

常见的概率图模型中，哪些是生成式模型，哪些是判别式模型？

速记：生成式模型：朴素贝叶斯、贝叶斯网络、pLSA、LDA等。判别式模型：最大熵模型、隐马尔可夫模型、条件随机场。

马尔可夫模型

###最大熵马尔可夫模型为什么会产生标注偏置问题？如何解决？

速记：原因：局部归一化的影响。解决：条件随机场

详细：由于局部归一化的影响，隐状态会倾向于转移到安歇后续状态可能更少的状态上，以提高整体的后验概率。这就是标注偏置问题。条件随机场在最大熵马尔可夫模型的基础上，进行了全局归一化，从而解决了局部归一化带来的标注偏置问题。

主题模型

###常见的主题模型有哪些？介绍其原理

速记：pLSA是用一个生成模型来建模文章的生成过程。LDA可以看作pLSA的贝叶斯版本。

详细：看书。

如何确定LDA模型的主题个数？

速记：利用验证集对超参数进行选择，常用的评估指标是困惑度。

详细：在文档集合D中，模型的困惑度被定义为
$$perplexity(D)=exp-\frac{{\sum }_{d=1}^M\log p(w_d)}{{\sum }_{d=1}^M{N}_d}$$
其中M为文档总数，$w_d$为文档d中单词所组成的词袋向量，$p(w_d)$为模型所预测的文档d的生成概率，$N_D$为文档d中单词的总数。

可以取验证集的困惑度极小值点对应的主题个数作为超参数。

如何用主题模型解决推荐系统中的冷启动问题？

冷启动问题：指在没有大量用户数据的情况下如何给用户进行个性化推荐，目的是最优化点击率、转化率或用户体验。

冷启动一般分为用户冷启动、物品冷启动和系统冷启动三大类。

没有难度，实际内容，几乎不存在理解，详细看书。