本文是3G实验室2024级二面题解，包含小车问题、笨小猴、拯救oibh总部等7道题目。作者分享了自身解题思路和代码实现，如小车问题需数学计算，笨小猴用哈希表解决，拯救oibh总部用深度搜索算法等，借此总结做题经验。
3G实验室2024级二面题解
前言
本次二面题对我自身而言还是十分有难度的，在考核之时只能写出四道，其中题目对我自身代码实现能力,理解题意能力也是一个极大的考验，也借此机会找到自己在学习上的不足。因此将此次二面题目总结为博客一篇，写出我个人对于题目的理解，以此总结自身做题经验，巩固自身进度。
1.小车问题
题目描述
甲、乙两人同时从 A 地出发要尽快同时赶到 B 地。出发时 A 地有一辆小车，可是这辆小车除了驾驶员外只能带一人。已知甲、乙两人的步行速度一样，且小于车的速度。问：怎样利用小车才能使两人尽快同时到达。
输入格式
仅一行，三个实数，分别表示 AB 两地的距离 s，人的步行速度 a，车的速度 b。
输出格式
两人同时到达 B 地需要的最短时间，保留 6 位小数。
样例输入 #1
120 5 25
样例输出 #1
9.600000
提示
数据规模与约定
对于 100% 的数据，保证 0≤s,a,b≤10^9。
解题思路
作为第一道签到题，就让我完全没有思路，模拟的过程在代码实现上没有难度，只是在解题上对我来说有数学难度。首先，我们要知道的是，无论采取怎么样的策略，甲乙两个人必将同时到达，即先载乙到半路，再让汽车回头载上甲，使得甲乙到达的时间为相同的。
那么我们假设甲中途的下车点为C，那么：
车从A到C的时间：Ta→c = S / b ；
又由于甲乙的步行速度是一样的，那么就意味着，甲乙的运动路程是对称的，如图
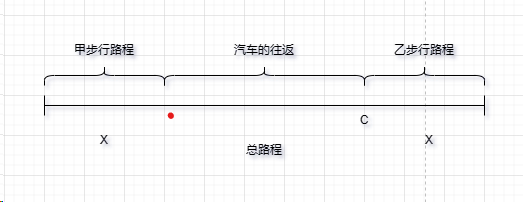
那么这个图一出来，其实方程也不难列出了x/a=(s-2x+s-x)/b，解得x=2as/(3a+b),知道了x,也就不难知道t=x/a+(s-x)/b。OK，知道了如何进行计算，我们马上用代码实现这个过程。
代码实现
#include <stdio.h>
int main() {
double a, b, s, t ,x;
scanf("%lf %lf %lf",&s,&a,&b);
x=2*a*s/ (3*a+b);
t= x/a + (s-x)/b;
printf(" %.6lf ",t);
return 0;
}
2.笨小猴
题目描述
笨小猴的词汇量很小，所以每次做英语选择题的时候都很头疼。但是他找到了一种方法，经试验证明，用这种方法去选择选项的时候选对的几率非常大！
这种方法的具体描述如下：假设 maxn 是单词中出现次数最多的字母的出现次数，minn 是单词中出现次数最少的字母的出现次数，如果maxn - minn是一个质数，那么笨小猴就认为这是个 Lucky Word，这样的单词很可能就是正确的答案。
输入格式
一个单词，其中只可能出现小写字母，并且长度小于 100 100 100。
输出格式
共两行，第一行是一个字符串，假设输入的的单词是 Lucky Word，那么输出 Lucky Word，否则输出 No Answer；
第二行是一个整数，如果输入单词是 Lucky Word，输出 maxn-minn 的值，否则输出 0。
样例输入 #1
error
样例输出 #1
Lucky Word
2
样例输入 #2
olympic
样例输出 #2
No Answer
0
解题思路
这道题就是一道简单的用哈希表解决的问题，在考试的时候，没看清题目的要求，导致差值在非质数数还输出他们差值的结果导致最后修改的时候，没来得及重新提交，少拿了八十分，这个故事告诉我们审题需谨慎。（哭脸）
在这道题里面，我们只需要统计给出字符串各自字母的数字，再在哈希表中找出最大和最小值的，再进行一个简单的质数判断。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int num(int nums){
if(nums == 0||nums == 1){
return 0;
}
for(int i=2;i<= sqrt(nums)/2;i++){
if(nums%i==0){
return 0;
}
}
return 1;
}
int main() {
char s[100];
scanf("%s",s);
int len = strlen(s);
int hash[26]={0};
for(int i=0;i<len;i++){
hash[s[i]-'a']++;
}
int max=0,min=100;
for(int i=0;i<26;i++){
if(hash[i]==0){
continue;
}
max=fmax(hash[i],max);
min=fmin(hash[i],min);
}
int res = max-min;
if(num(res)){
printf("Lucky Word\n");
printf("%d\n",res);
return 0;
}
printf("No Answer\n");
printf("0\n");
return 0;
}
顺带提一句，这个质数的判断显然不是算法的最优解，通过埃式筛能够更快的进行相关质数的筛查。
void sieve_of_eratosthenes(int n) {
// 创建一个数组，用于标记是否为素数
int prime[n+1];
// 初始化数组，假定所有数都是素数
for (int i = 0; i <= n; i++) {
prime[i] = 1;
}
prime[0] = 0, prime[1] = 0;
// 埃拉托斯特尼筛法
for (int i = 2; i <= sqrt(n); i++) {
if (prime[i]) {
for (int j = i * i; j <= n; j += i) {
prime[j] = 0; // 将i的倍数标记为非素数
}
}
}
}
3.拯救oibh总部
题目背景
oibh 总部突然被水淹没了！现在需要你的救援……
题目描述
oibh 被突来的洪水淹没了，还好 oibh 总部有在某些重要的地方起一些围墙。用 * 号表示，而一个四面被围墙围住的区域洪水是进不去的。
oibh 总部内部也有许多重要区域，每个重要区域在图中用一个 0 表示。
现在给出 oibh 的围墙建设图，问有多少个没被洪水淹到的重要区域。
输入格式
第一行为两个正整数 x , y x,y x,y。
接下来
x
x
x 行，每行
y
y
y 个整数，由 * 和 0 组成，表示 oibh 总部的建设图。
输出格式
输出没被水淹没的 oibh 总部的 0 的数量。
样例输入 #1
4 5
00000
00*00
0*0*0
00*00
样例输出 #1
1
样例 #2
样例输入 #2
5 5
*****
*0*0*
**0**
*0*0*
*****
样例输出 #2
5
思路
本题使用的是dfs，深度搜索算法，我们首先是先遍历这个二维数组最外圈的空间，如果有空间，那么就用递归进行深入探索，我们可以存入两个长度为4的数组，代表上下左右的方向，对可以经过的地方进行标记。直至遍历结束，只要在地图中没有被标记的地方即为没有被洪水淹没的地方。
代码实现
#include<stdio.h>
char ch;
int x, y, ans, map[550][550];
int dx[4] = {1, -1, 0, 0},dy[4] = {0, 0, 1, -1};//dx,dy是上下左右四个方向
void dfs(int m,int n) {
if(m < 0 ||n < 0 || m > x + 1 || n > y + 1 || map[m][n]) {
return;
} //如果越界或有障碍就回溯
map[m][n] = 2;
for(int i = 0; i < 4; i++) {
dfs(m + dx[i],n + dy[i]);
} //上下左右搜索
}
int main()
{
scanf("%d %d", &x, &y);
for(int i = 1; i <= x; i++) { //处理成数字地图
for(int j = 1;j <= y; j++) {
scanf(" %c", &ch);
if(ch == '0') {
map[i][j] = 0;
} else {
map[i][j] = 1;
}
}
}
dfs(0, 0); //开始递归
for (int i = 1; i <= x; i++) {
for (int j = 1; j <= y; j++) {
if (!map[i][j]) {
ans++;
}
}
} //寻找没有被洪水袭击的点即未被染色的点
printf("%d", ans);
return 0;
}
4.队列安排
题目描述
一个学校里老师要将班上 N N N 个同学排成一列，同学被编号为 1 ∼ N 1\sim N 1∼N，他采取如下的方法：
-
先将 1 1 1 号同学安排进队列，这时队列中只有他一个人；
-
2 ∼ N 2\sim N 2∼N 号同学依次入列，编号为 i i i 的同学入列方式为：老师指定编号为 i i i 的同学站在编号为 1 ∼ ( i − 1 ) 1\sim(i-1) 1∼(i−1) 中某位同学（即之前已经入列的同学）的左边或右边；
-
从队列中去掉 M M M 个同学，其他同学位置顺序不变。
在所有同学按照上述方法队列排列完毕后，老师想知道从左到右所有同学的编号。
输入格式
第一行一个整数 N N N，表示了有 N N N 个同学。
第 2 ∼ N 2\sim N 2∼N 行，第 i i i 行包含两个整数 k , p k,p k,p，其中 k k k 为小于 i i i 的正整数， p p p 为 0 0 0 或者 1 1 1。若 p p p 为 0 0 0，则表示将 i i i 号同学插入到 k k k 号同学的左边， p p p 为 1 1 1 则表示插入到右边。
第 N + 1 N+1 N+1 行为一个整数 M M M，表示去掉的同学数目。
接下来 M M M 行，每行一个正整数 x x x，表示将 x x x 号同学从队列中移去，如果 x x x 号同学已经不在队列中则忽略这一条指令。
输出格式
一行，包含最多 N N N 个空格隔开的整数，表示了队列从左到右所有同学的编号。
样例输入 #1
4
1 0
2 1
1 0
2
3
3
样例输出 #1
2 4 1
解题思路
在这道题中，关键词的提示已经是十分到位，入和出，就直接联想到了链表的相关操作，每个学生都有左右手，就让我又想起了，双向链表充当学生的两只手，我们只需要根据题目给出的数字再在相关位置进行插入，然后再读取所去掉的同学的下标。由于链表中的删除操作还是相对比较麻烦的，所以我们可以在结构体之中存入一个flag，然后再遍历数组模拟的链表时，读取节点的flag，若为0就进行输出。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#include <ctype.h>
typedef struct student {
int l, r;
int flag;
}s;
s stu[1000000];
void add(int i, int k, int flag) {
if (flag == 1) { //右边
stu[i].l = k;
stu[i].r = stu[k].r;
stu[k].r = i;
stu[stu[i].r].l = i;
} else { //左边
stu[i].r = k;
stu[i].l = stu[k].l;
stu[k].l = i;
stu[stu[i].l].r = i;
}
}
int main() {
int n, k, p, m;
scanf("%d", &n);
for (int i = 0; i <= n; i++) {
stu[i].flag = 0;
}
stu[0].r = stu[0].l = 0;
add(1, 0, 1);
for (int i = 2; i <= n; i++) {
scanf("%d %d", &k, &p);
add(i, k, p);
}
scanf("%d", &m);
for (int i = 0; i < m; i++) {
scanf("%d", &k);
stu[k].flag = 1;
}
for (int i = stu[0].r; i != 0; i = stu[i].r) {
if (stu[i].flag == 0) {
printf("%d ",i);
}
}
return 0;
}
5. 句子反转
题目描述
给定一行句子，每个词之间用空格隔开，要么是全小写英文单词，要么是全大写英文单词，要么是自然数。
要求将这些单词倒序输出。而且对于每个单词，如果是小写词，应当转为大写；如果是大写词，应当转为小写；如果是自然数，应该倒转输出。
举一个例子：
we choose TO go 2 the 123 moon
程序应当输出：
MOON 321 THE 2 GO to CHOOSE WE
输入格式
仅一行，即需要反转的句子。
输出格式
仅一行，表示程序对句子的处理结果。
样例输入 #1
we choose TO go 2 the 123 moon
样例输出 #2
MOON 321 THE 2 GO to CHOOSE WE
对于 %100的数据，句子中包含的单词数量不超过 1000，每个单词长度不超过 6。
解题思路
一看到这道题，就联想到了之前组内测试的时候的题目：
与此题相同的处理方式，我们要将字符串中的单词进行一个顺序的反转，而遇到数字则还需要逆向输出数字的顺序。那么我的思路就是，将字符串整体进行反转操作：
noom 321 eht 2 og OT esoohc ew
然后使用双指针，右指针不断遍历字符串直到读取到 ，然后将左指针和右指针涵盖的单词内容再一部分进行反转。由于我们在先前的操作中，已经将数字进行反转得到我们想要的内容，那么我们不需要对数字进行操作，所以我们在读取到 的时候，可以检测前一个字符串是为数字还是字母。我们可以用isdigit判断其是否为数字，若为数字则不需要其在进行反转的操作。而对于将字母大小写进行转化，我们只需要在双指针的遍历过程中，使用toupper和tolower进行大小写转化的实现。
思路存在，以下是代码实现：
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#include <ctype.h>
void rever(char* s,int left,int right){
while(left<=right){
char temp =s[left];
s[left]=s[right];
s[right]=temp;
left++,right--;
}
}//字符串反转函数
int main(){
char s[6000];
gets(s);
int len = strlen(s);
rever(s,0,len-1);
int left=0;
for(int i=0;i<=len;i++)//注意=的存在
{
if(islower(s[i])){
s[i]=toupper(s[i]);
}
else if(isupper(s[i])){
s[i]=tolower(s[i]);
}//对字符串进行大小写转化
if((isdigit(s[i-1]))&&(s[i]==' '||s[i]=='\0')){
left=i+1;
}else if((s[i]==' '||s[i]=='\0')){
rever(s,left,i-1);
left=i+1;
}//读到空格或者字符结尾就将字符反转
}
printf("%s",s);
return 0;
}
6.明明的随机数
题目描述
明明想在学校中请一些同学一起做一项问卷调查，为了实验的客观性，他先用计算机生成了 N N N 个 1 1 1 到 1000 1000 1000 之间的随机整数 ( N ≤ 100 ) (N\leq100) (N≤100)，对于其中重复的数字，只保留一个，把其余相同的数去掉，不同的数对应着不同的学生的学号。然后再把这些数从小到大排序，按照排好的顺序去找同学做调查。请你协助明明完成“去重”与“排序”的工作。
输入格式
输入有两行，第 1 1 1 行为 1 1 1 个正整数，表示所生成的随机数的个数 N N N。
第 2 2 2 行有 N N N 个用空格隔开的正整数，为所产生的随机数。
输出格式
输出也是两行，第 1 行为 1个正整数 M，表示不相同的随机数的个数。
第 2行为 M个用空格隔开的正整数，为从小到大排好序的不相同的随机数。
样例输入 #1
10
20 40 32 67 40 20 89 300 400 15
样例输出 #1
8
15 20 32 40 67 89 300 400
解题思路
这是一道排序加去重的题目，我们可以直接使用qsort函数对数组进行排序，然后再遍历数组对比前后两个是否相同，使用原地进入的方式。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
int cmp(const void* a,const void* b){
return *(int*)a-*(int*)b;
}
int main(){
int n;
scanf("%d",&n);
int a[n];
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
qsort(a,n,sizeof(int),cmp);//用qsort实现排序
int count=0;
for(int i=1;i<n;i++){
if(a[i]!=a[i-1]){
a[++count]=a[i];
}
}
printf("%d\n",count+1);
for(int i=0;i<count+1;i++){
printf("%d ",a[i]);
}
return 0;
}
7.小A的糖果
题目描述
小 A 有 n n n 个糖果盒，第 i i i 个盒中有 a i a_i ai 颗糖果。
小 A 每次可以从其中一盒糖果中吃掉一颗，他想知道，要让任意两个相邻的盒子中糖的个数之和都不大于 x x x，至少得吃掉几颗糖。
输入格式
输入的第一行是两个用空格隔开的整数，代表糖果盒的个数 n n n 和给定的参数 x x x。
第二行有 n 个用空格隔开的整数，第 i 个整数代表第 i i i 盒糖的糖果个数 a i a_i ai。
输出格式
输出一行一个整数，代表最少要吃掉的糖果的数量。
样例输入 #1
3 3
2 2 2
样例输出 #1
1
样例输入 #2
6 1
1 6 1 2 0 4
样例输出 #2
11
样例输入 #3
5 9
3 1 4 1 5
样例输出 #3
0
解题思路
该题是一个较为简单的贪心算法，从提示出发，我们可以知道，在处理篮子中的糖果时，最优解其实为优先拿走第二个篮子中的糖果，这样子可以同时减少两个组的糖果数量，而对于数组中第一个篮子的糖果数量，则需要进行特殊判断，先减少至满足条件的个数，再以两个篮子一组进行判断。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#include <ctype.h>
int main() {
int n , x;
scanf("%d %d",&n,&x);
int a[n];
for(int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
long long sum = 0;
if(a[0] > x) {
sum += a[0] - x;
a[0] = x;
}
for(int i = 1; i < n; i++) {
if(a[i-1] + a[i] > x) {
sum += (a[i-1] + a[i] - x);
a[i] = x - a[i-1];
}
}
printf("%ld", sum);//要用long long 才能承接结果的大小
return 0;
}
0
解题思路
该题是一个较为简单的贪心算法，从提示出发，我们可以知道，在处理篮子中的糖果时，最优解其实为优先拿走第二个篮子中的糖果，这样子可以同时减少两个组的糖果数量，而对于数组中第一个篮子的糖果数量，则需要进行特殊判断，先减少至满足条件的个数，再以两个篮子一组进行判断。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#include <ctype.h>
int main() {
int n , x;
scanf("%d %d",&n,&x);
int a[n];
for(int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
long long sum = 0;
if(a[0] > x) {
sum += a[0] - x;
a[0] = x;
}
for(int i = 1; i < n; i++) {
if(a[i-1] + a[i] > x) {
sum += (a[i-1] + a[i] - x);
a[i] = x - a[i-1];
}
}
printf("%ld", sum);//要用long long 才能承接结果的大小
return 0;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
