机器学习基石--------feasibility of learning

机器学习基石 ------- feasibility of learning

1.Learning is impossible

2.Probability to the Rescue

3.Connect to learning

---

Learing is impossible

对于上述问题，当学习样本有限（只有六张） 同时特征较为模糊时（根据左上角 是否对称）的时候 很难获得一个确切的判别式。

再来看一个例子：

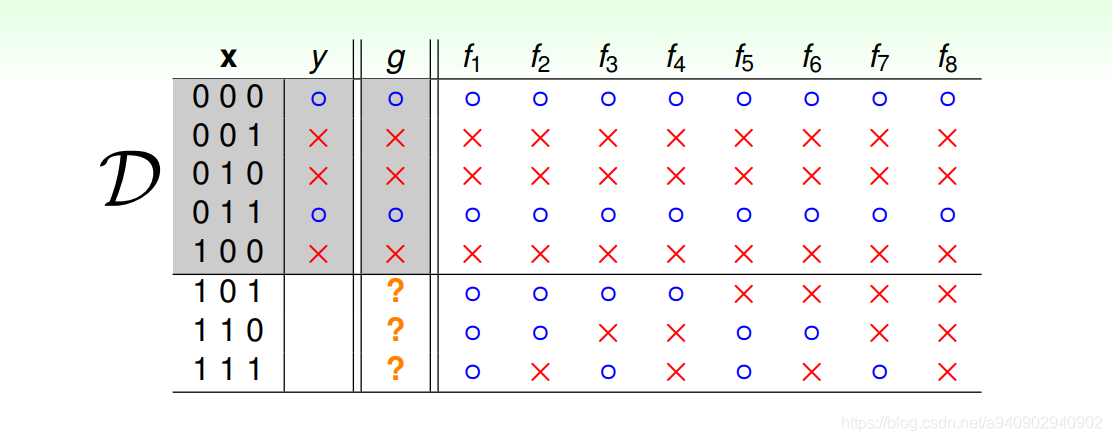
对于输入样本为3维的二元分类问题 输入可能有8种 每一个可能有两种输出 总共可能的按照这种方法生成hypothesis 有2⁸种
对于给出的5种可能 在hypothesis set中满足这样的E_in的h有2³种
对于训练样本D 在D的范围内我们可以保证f（x）=g（x），但是在D的范围外，如上图中最后三种可能 f可能的预测结构多达8种 我们不能保证究竟哪一种是真正的g 仿佛在这些资料中没有学到什么东西 因为我们想要的不是在给定的资料上的预测结果 而是想要在资料以外的预测和不知道的那个f（x）是否一样

此时 如果仅仅给出x∈D 的若干种训练样本 以及对应的预测结果g（x） 不加其他的限制 我们是无法得到一个稳定的f（x）在D的范围外拟合g(x) 而这恰恰是我们想要做到的 即 No Free Lunch问题

Probability to the Rescue

既然无法推论出在训练样本之外的判别式的表现 那么是否可以在增加一些限定条件之后能够得到判别式对于训练样本之外的样本的表现呢？或者说我们根据当前的样本信息得到一些额外的信息呢？ 例如 在罐子里有绿色和橙色两种小球的时候 橙色小球占比为μ ，对于我们而言是未知的，我们如何根据当前已有的信息来得到μ的信息呢 罐子里一颗颗弹珠就像是我们想要预测的问题的资料 从里面抓取一把资料 可以看做我们的训练样本 对于二分类问题 可以把弹珠涂成两种颜色 不同颜色代表不同label

我们可以采取采样的方式 根据Hoeffding不等式可知 当采样样本N足够大的时候，采样样本中橘色小球所占比例v是十分接近我们希望所得的罐子内的橘色小球所占比例μ的，具体关系如上述不等式所示，其中ε代表我们可以接受的误差，可想而知 在同等的样本的情况下 我们能够容忍的误差越大 v等于μ的概率就越大，同样的样本数越多 ，在容忍误差一定的情况下 v和μ相等的概率越大
我们的目的是得到μ，恰巧霍夫丁不等式得到v和μ误差为ε的几率是和μ无关的 因此 可以通过这个式子得到几率的上限

Connect to learning

下面我们就把在罐子里面抽取弹珠和learning联系起来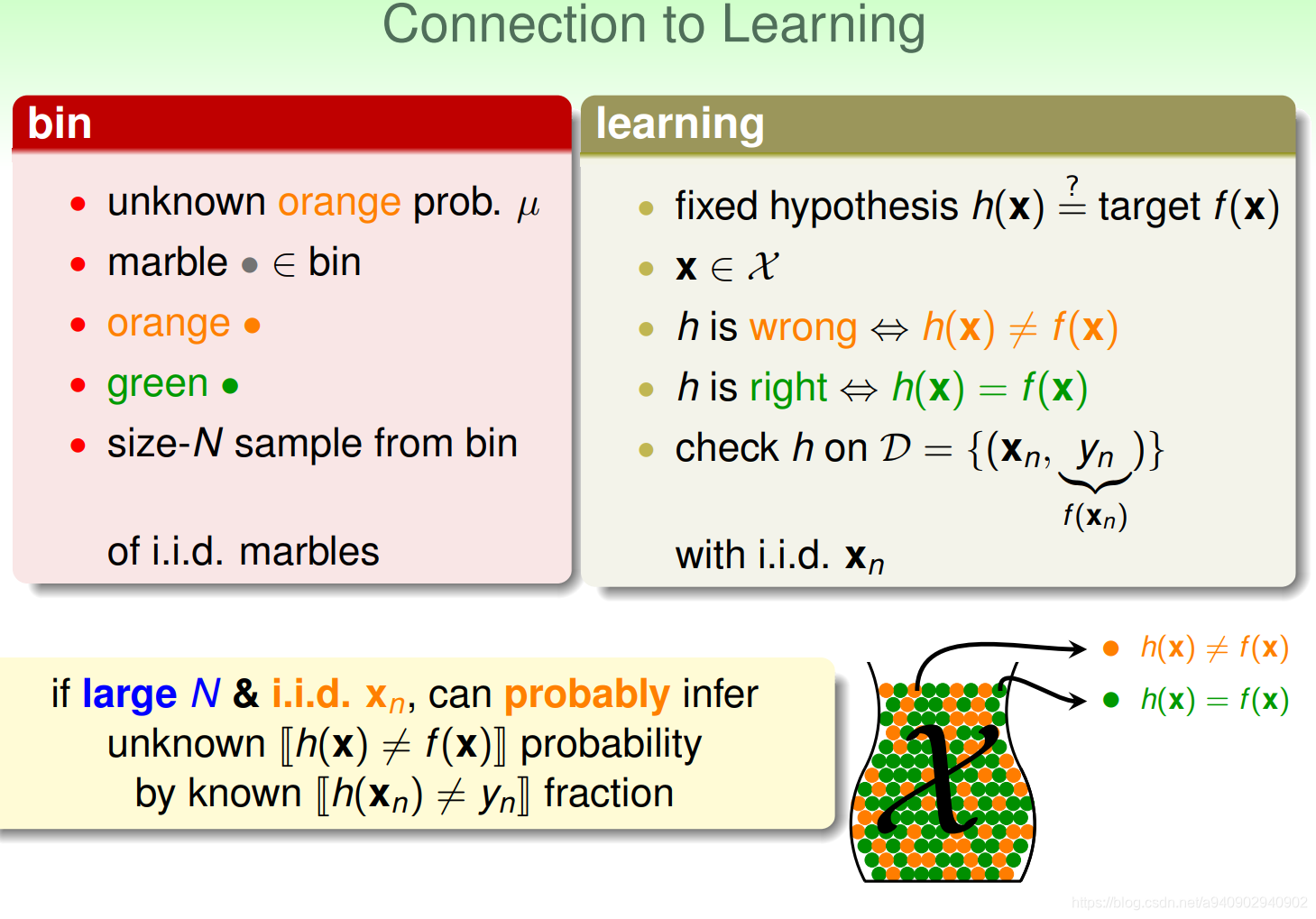

（1）首先从我们的目标出发,
在抽取弹珠时我们不知道的是那个μ，即罐子中橘色的比例
同理在learning中我们不知道的是目标函数f，当然也就不知道在某个x上的f（x）值,我们想要得到的是在hypothesis set中选择一个hypothesis 使得 在x点上h(x)和f（x）相等 ，我们不知道h(x)和f（x）（也就是y值）相等的概率
（2） 从x的角度出发
我们可以把x看做是一个个的弹珠 当我们手上有一个hypothesis的时候 我们在一个个x上使用h(x)和f(x)作比较如果二者相等 就涂成橘色 不相等就涂成绿色 有一点要注意 这里的x 也就是弹珠 也就是我们所拥有的训练样本资料 当资料没有噪声的时候 x对应的label 即f(x) 的值 这个时候N代表的就是我们在罐子里面抽取的弹珠数 也就是在训练样本的数量
（3）结论
当样本服从相同分布 如果我们抽样够大 （训练样本够大）可以使用训练样本上的h(x)和y的差异（训练样本的误差）来估计h（x）和f(x)在我们未知的样本上的差异

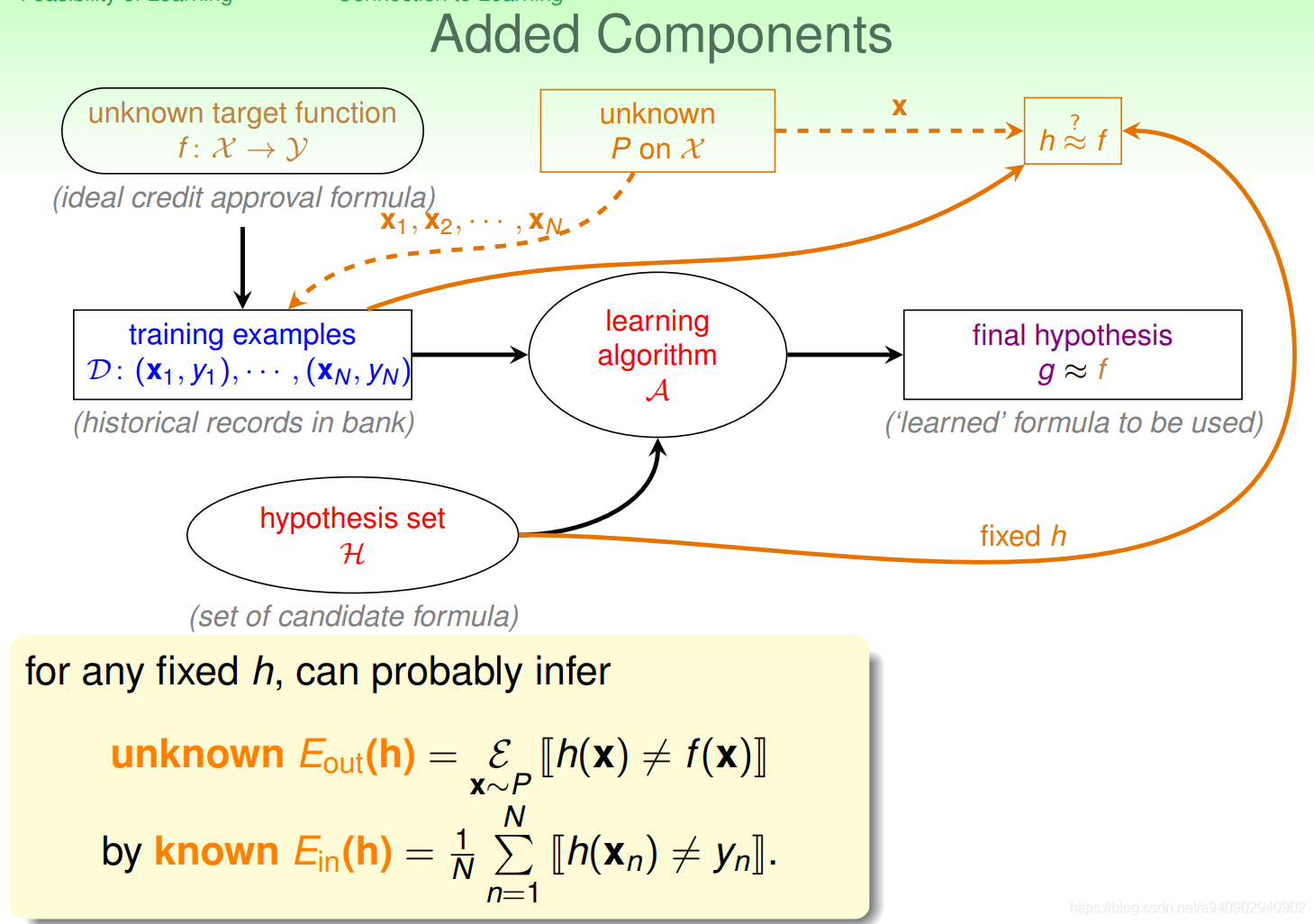
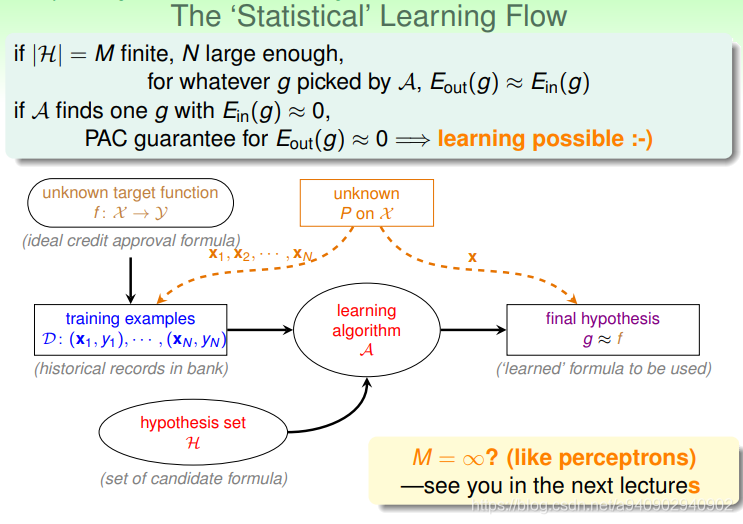
我们有一个不知道的分布P ，它产生了资料x1，x2，x3…(抽取了一把弹珠) 同时在learning flow中得到的hypothesis set中拿到一个hypothesis
E_in 是在抽取的资料 x1，x2…上h（x）和f(x)是否一样
E_out 是在整个资料上h（x）和f(x)是否一样
根据霍夫丁不等式可得 如果N足够大 同时罐子中的数据分别和抽取的样本分布一致 则 E_out 可能和
E_in很接近
那么对于我们的目标 是想要E_out 很小 那么如果能够保证E_in很小 则 E_out可能也很小，但是我们要注意的是 上述所有都是基于我们选择了一个hypothesis 在有一个hypothesis的情况下 当E_in很小的时候 E_out也很小 这像是使用验证集做验证的情况 在我们学得了一个hypothesis，使用一部分服从某一分布的数据在这个hypothesis上做验证 如果E_in很小 那么在同分布的其他数据上这个hypothesis 的E_out也会很小

但是机器学习是要在一系列的hypothesis set中选择一个hypothesis ，也就是说此时有很多的hypothesis
我们这时候可以想象有很多个罐子 对应很多个hypothesis 在每个罐子中抽出若干的弹珠，如果其中一个全是绿色 也就是在这些资料上 这个hypothesis（x） 和f（x）全都相等 一种可能是它确实对位置分布产生的所有数据的拟合能力都很好 同时也有可能恰巧是选取到的这些数据对于这个hypothesis很拟合 仅此而已
根据霍夫丁不等式 对于一个固定的hypothesis E_in和E_out差距很大这件事发生的概率很小 但是当hypothesis有选择 在所有的hypothesis 中任意一个出现E_in和E_out差距很大这件事发生的概率会被扩大 就像一个人丢铜板 丢到十次全部朝上的概率很小 但是10000个人一起丢 其中有一个人丢到全部都是朝上的概率被大大扩大了

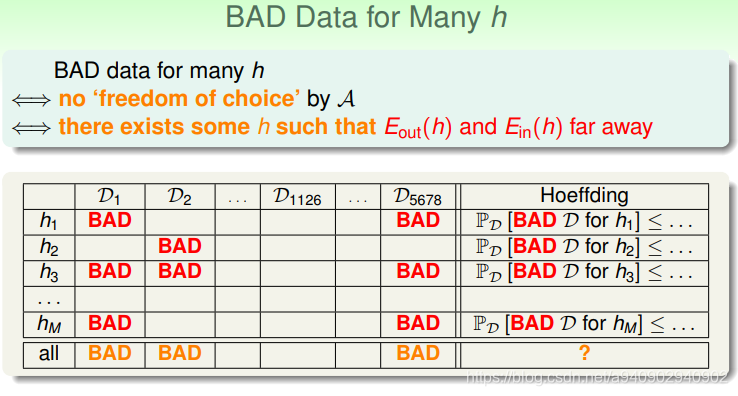
霍夫丁不等式保证的是抽取一把资料 对于一个固定的hypothesis 这笔资料是bad的几率很小 即 D1，D2…这些格中是bad的几率很小
不同的hypothesis 对于不同的D1，D2是否是bad可能不同 但是霍夫丁不等式保证 每一行是bad的格很少
只有当在像D1126这样的资料上 才能够在hypothesis set中安心选择一个E_in较小的 因为此时无论选择哪个h 其E_in和E_out都相近 此时E_in较小 才能推出E_out较小

霍夫丁不等式在有限数量的Hypothesis上的延伸 对于每一个H 都可以根据霍夫丁不等式得出 E_in和E_out不相近的概率
那么对于所有的H，根据union bound 可以得出在所有H上的E_in和E_out不相等的概率 如果这个概率很小 那么我们就可以安心选择任意一个在E_in上很小的hypothesis 作为 拟合f的g
当M有限 并且N很大时 可得P_D[bad D]确实很小
这就保证了不管hypothesis set上怎么选 选到的hypothesis E_in和E_out都很接近 因此学习算法可以无顾忌的在hypothesis set上选择 E_in较小的h