【CFD理论】N-S方程推导

目录

N-S方程

控制体内动量变化率

流入控制体的动量

控制体所受合力

体积力

表面力

整理方程

微分形式

化简

---

N-S方程

针对控制体，有动量守恒方程如下：

控制体内流体总动量的增量= 流入控制体的流体动量+外界的力产生的动量增量

上式除以时间后得到以下等式，等式分为三个部分

控制体内动量变化率

密度乘体积微元得到质量，乘速度矢量再积分就是控制体的动量变化。最后再对时间求偏导即可得到下式

流入控制体的动量

流体的流速点乘控制体面积微元法向量，得到流入控制体的体积。再乘密度得到质量，最后再乘一个速度矢量积分得到动量。

控制体所受合力

其中第二部分分为体积力与表面力两部分

表面力分为压力和粘性力。粘性正应力垂直于控制面，粘性切应力相切于控制面

体积力

设受到的体积力为f，易得到以下表达式

表面力

表面力分为压力与粘性力

压力易得，表达式如下：

粘性力非常复杂，本文不进行深入推导，暂用Fvis代替

整理方程

微分形式

把上面得到的表达式整理成N-S方程如下：

得到积分形式的N-S方程。

显然N-S方程在直角坐标系中可分为三个方向的方程，为便于分析，下文针对X方向上的分量进行研究，得到方程如下：

根据奥高定律，可以将控制体面积分变化为控制体体积分，进而可以去掉积分符号。

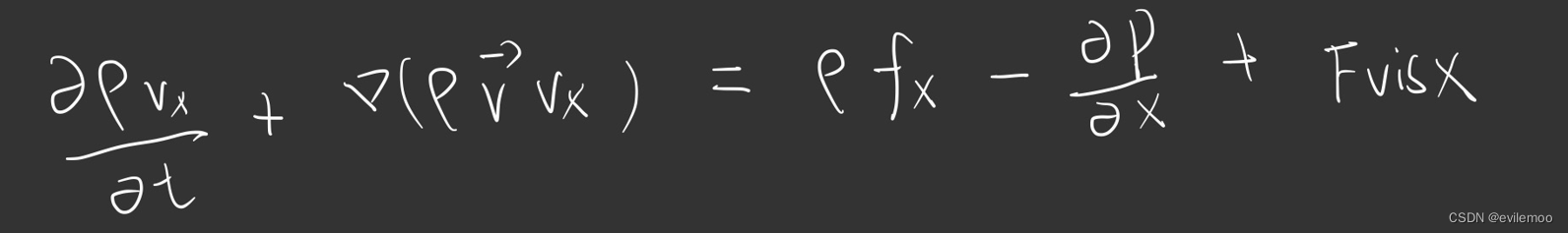
化简

等式左边第二项，展开如下

等式左边进一步展开

把相似项整理到一起

由连续性方程，可以把左边一块消去，最终得到眼熟的形式如下：

粘性项如下，非常复杂，此处仅给出结果

一般的，非强压缩性的情况下，后面这一项可以省去

最终得到常见的N-S方程形式如下：

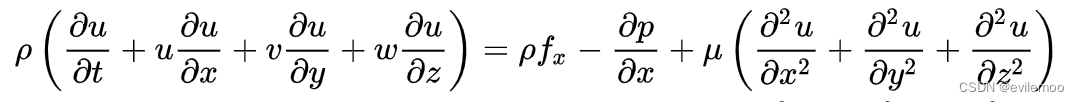
同样的，y方向与z方向如下：

把三个方向整合起来，矢量形式的方程如下：