排序算法之分配排序（线性时间排序）

分配排序的基本思想：排序过程无须比较关键字，而是通过"分配"和"收集"过程来实现排序.它们的时间复杂度可达到线性阶：O(n)。

下面介绍三种线性排序的算法：

1：计数排序

2：基数排序

3：桶排序

一：计数排序

1：原理

计数排序假设：N个输入元素中的每一个都是介于0~k之间的整数，此处k为某个整数。当k=O(n)时，计数排序的运行时间O(n)。

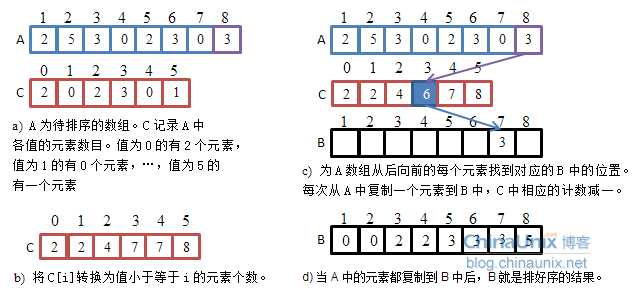
算法思想：对每一个输入元素x，确定出小于x的元素个数；有了这一个信息，就可以直接把x放在最终输出数组的位置上。如果有m个小于x，那x就放在m+1的位置上。

计数排序要求被排序元素都是整数型变量，即元素能用数组的指标表示

（1）统计个元素 i 的个数

（2）计算不超过 i 包括 i 的元素的个数

（3）将元素 i 放入适当的位子。

2：实现

void CountSort(int arr[],int n,int k)
{
    int i;
    int *B = (int *)malloc(n*sizeof(int));
    if(!B){
        printf("malloc error!");
        exit(1);
    }
    int *C = (int *)malloc((k+1)*sizeof(int)); //因为要存储0--k个数据
    if(!C){
        printf("malloc error!");
        exit(1);
    }

    for(i=0;i<=k;i++)   //将数组元素初始化为0
        C[i] = 0;
    for(i=0;i<n;i++){   //对C数组的每个元素开始计数
        C[arr[i]]++;
    }

    for(i=1;i<=k;i++)   //找到正确的i位置
        C[i]= C[i]+C[i-1];


    for(i=n-1;i>=0;i--){    //利用临时数组B存储有序数组
        B[C[arr[i]]-1] = arr[i];    //这里必须让C[arr[i]]-1！因为数组是从0开始计数的，而C统计的是个数
        C[arr[i]] -= 1;
    }

    for(i=0;i<n;i++){   //返回数据
        arr[i]=B[i];
    }

}

3：分析

计数排序的一个重要性质：稳定排序（具有相同值的元素在输出数组中的相对次序与它们在输入数组中的相对次序相同）。

时间复杂度：总的时间复杂度为O(n+k)，当k=O(n)时，运行时间为O(n)。

二：基数排序

1：原理

1）多关键字的排序

如果待排序的每个元素都为一个d位数，每个数位可以取k种可能的值，（比如十进制里的246是一个3位数，每个数位可以取0~9共10种可能的值。）第1位为最低位，而第d位为最高位，我们便可以依次对每一个位进行排序，当所有的位数都排好序时后，所有的元素也都排好序了。下面演示一个对三位十进制数的排序过程：

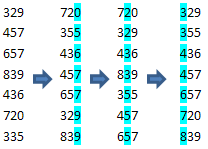
注意到每次排序的结果必须是稳定的，否则会出错。比如上例中，在排好第二位后，329在355的前面，之后在对最高位排序时，必须保持这个次序。利用不稳定的排序算法对最高位排序时，329可能会排到355的后面，因为最高位是相等的，都是3。
所以基数排序的伪代码为：

RADIX_SORT(A, d) 
{
    for i = 1 to d
        use a stable sort to sort array A on digit i
}

2）链式基数排序

具体做法

（1）先从最低位关键字开始，依次到最高位进行链队列排序

（2）“分配”：将每一个关键字分配到十个队列中对应的队列，从前往后扫描，比如278和008,278在前，所以f[7]指向278，以后的最低位为8时放到后面。保证了稳定性。

（3）“收集”：按照队列从前往后，比如第一趟时，e[0]和f[3]连接，串成一个新序列。

（4）依次从低位到高位进行“分配”“收集”

2：实现（暂无）

1）多关键字的排序

算法可以按照最高优先法（MSD）和最低优先法（LSD）来实现。两种排序有不同特点：

按照MSD进行排序，必须将序列逐层分割成若干子序列，然后对各子序列分别进行排序；按照LSD进行排序时，不必分成子序列，对每个关键字都是整个序列参加排序，但排序是必须要用稳定的排序方法。

代码略。

2）链式基数排序

详细代码见《数据结构》P288

3：分析

1）多关键字的排序

前面我们已经介绍过计数排序，它是稳定的，所以我们可以用它来实现基数排序。这样上面代码中每次迭代的代价为Ө(n+k)，基数排序总的运行时间可达到Ө(d*(n+k))，其中d为元素的位素，k为每位可取的值。当d为常数，k为O(n)时，基数排序有线性时间。

2）链式基数排序（n个记录，d个关键字，每个关键字取值范围rd）

每一趟分配的时间复杂度为O(n)，每一趟收集的时间复杂度为O(rd)，对整个排序需要d趟分配和收集----总的时间复杂度为O(d(n+rd))。

缺点：所需辅助空间为2rd个队列指针；又由于链表作为存储结构，还给每个数据增加了指针域空间（一共增加了n个指针域）。

评比：

基数排序是否比基于比较的排序（如快速排序）更好呢？看上去基数排序在b=O(lg(n))，r≈lg(n)时运行时间为Ө(n)，渐近优于快速排序的平均情况Ө(n*lg(n))，但是基数排序的Ө(n)里隐含的常数因子很大，所以基数排序并不一定快于快速排序。而且基数排序所使用的计数排序不是原地排序，所以需要额外的内存。

三：桶排序

1：原理

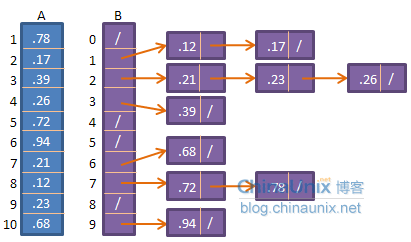
A为待排序的数组，所有的元素都均匀而独立地落在[0,1)的区间里。一个辅助数组B，分成与A中元素个数相同的区间，每个区间都称为一个桶，它是一个链表。我们将A中的元素A[i]放入到B[floor(n*A[i])]里， 比如A中共10个元素，值为0.1的元素就放到B[floor(10*0.1)]，即B[1]里的桶里。可以看到，B中每个桶里的元素都要大于其前一个桶 里的元素，比如B[6]里的元素都要比B[5]里的元素大。如果我们再对每个桶里的链表里的元素进行排序的话，我们便可以在B中得到一个有序数列。

2：实现

下面是伪代码：

BUCKET_SORT(A)
{
    n = A.length;
    for i = 1 to n
        insert A[i] into list B[floor(n*A[i])];
    for i = 0 to n-1;
        sort list B[i] with insertion sort;
      concatenate the lists B[0], B[1], ..., B[n-1] together in order
}

3：分析

即使输入数据不服从均匀分布，桶排序也可以线性时间内完成，只要输入数据满足以下性质：所有的桶的大小的平方和与总的元素数呈线性关系。