激活函数总结

激活函数的作用

  在神经网络中，激活函数的作用是能够给神经网络加入一些非线性因素，使得神经网络可以更好地解决较为复杂的问题。
  先举一个简单的例子，在做二分类时，我们的预测值$\hat{y}=w^{T}x+b$，其中w和b为参数，我们希望得到一个范围是（0,1）的概率值，而如果直接使用上式进行计算会导致预测值大于1或小于0，因此我们就需要套接一个激活函数，例如sigmoid函数，其值为（0,1）范围。
  再比如下面这个问题中：

  如上图所示，这是一个简单的线性分类问题，只需要一条直线就可以很好地分类。当我们碰到下图问题时，无法通过一条直线将样本分类出来，需要我们加入非线性因素才可以将样本分类好，而我们的激活函数就是我们要加入的非线性因素。

激活函数的软饱和、硬饱和、左饱和、右饱和

  假设h（x）是一个激活函数。
  1.当我们的n趋近于正无穷，激活函数的导数趋近于0，那么我们称之为右饱和。
  ${\lim }_{n\to +\infty }{h}^{\prime }\left(x\right)=0$
  2.当我们的n趋近于负无穷，激活函数的导数趋近于0，那么我们称之为左饱和。
  ${\lim }_{n\to -\infty }{h}^{\prime }\left(x\right)=0$
  当一个函数既满足左饱和又满足右饱和的时候我们就称之为饱和，典型的函数有Sigmoid，Tanh函数。
  3.对于任意的x，如果存在常数c，当x>c时，恒有$h^{\prime }(x)=0$，则称其为右硬饱和。如果对于任意的x，如果存在常数c，当x<c时，恒有$h^{\prime }(x)=0$,则称其为左硬饱和。既满足左硬饱和又满足右硬饱和的我们称这种函数为硬饱和。
  4.对于任意的x，如果存在常数c，当x>c时，恒有$h^{\prime }(x)$趋近于0，则称其为右软饱和。如果对于任意的x，如果存在常数c，当x<c时，恒有$h^{\prime }(x)$趋近于0,则称其为左软饱和。既满足左软饱和又满足右软饱和的我们称这种函数为软饱和。

常见的激活函数

a) Sigmoid函数

Sigmoid函数：

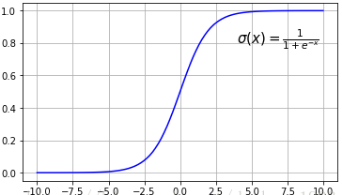
Sigmoid导数：

  Sigmoid函数的优点：1.求导容易。 2.Sigmoid函数的输出映射在(0,1)之间，单调连续输出范围有限，优化稳定可以用作输出层。
  缺点：1.由于其软饱和性，容易造成梯度消失问题。2.其输出没有以0为中心。

b) Tanh函数

Tanh函数：
  $\tanh \left(z\right)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$

Tanh函数导数：
  ${\tanh }^{\prime }\left(z\right)=1-(\tanh \left(z\right){)}^2$

  Tanh函数的优点：1.收敛速度比Sigmoid函数快。 2. 其输出以0为中心。
  缺点：还是出现软饱和现象，梯度消失问题并没有解决。

c）Relu函数

Relu函数：
  $g\left(x\right)=\max \left(0,x\right)$

Relu导数：
  $g^{\prime }\left(x\right)=\{\begin{array}{l}0x<0\\ 1x\ge 0\end{array}$

  Relu函数的优点：1.在SGD（随机梯度下降算法）中收敛速度够快。2.不会出现像Sigmoid那样梯度消失问题。3.提供了网络稀疏表达能力。4.在 无监督训练中也有良好的表现。
  缺点：1.不以0为中心。2.前向传导（forward pass）过程中，如果 x < 0，则神经元保持非激活状态，且在后向传导（backward pass）中「杀死」梯度。这样权重无法得到更新，网络无法学习。神经元死亡是不可逆的。

d）LReLU、PReLU与RReLU函数

  LRelu函数：抑制负的输入，原样输出正值。
LRelu函数：
  $g\left(x\right)=\max \left(0.01x,x\right)$
LRelu导数：
  $g^{\prime }\left(x\right)=\{\begin{array}{l}0.01x<0\\ 1x\ge 0\end{array}$
  LRelu的优点：缓解了Relu神经元死亡的问题。

PRelu函数：
公式：
  $g\left(x\right)=\max \left(\alpha x,x\right)$
  这里引入了一个随机的超参数α，它可以被学习，因为你可以对它进行反向传播。这使神经元能够选择负区域最好的梯度，有了这种能力，它们可以变成 ReLU 或 Leaky ReLU。负值部分的斜率是根据数据来定的，而非预先定义的。

RRelu函数：

  RReLU也是Leaky ReLU的一个变体。在RReLU中，负值的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU的亮点在于，在训练环节中，aji是从一个均匀的分布U(I,u)中随机抽取的数值。
  RReLU中的aji是一个在一个给定的范围内随机抽取的值，这个值在测试环节就会固定下来。

e）ELU激活函数：

  $f\left(x\right)=\{\begin{array}{l}xx\ge 0\\ \alpha \left(e^x-1\right)x<0\end{array}$

  右侧的线性部分能够缓解梯度消失,左侧的软饱和能够对于输入变化鲁棒.而且收敛速度更快.