完整笔记:http://www.gwylab.com/note-gans.html
———————————————————————
本章借鉴内容:
https://baike.baidu.com/item/%E5%A5%87%E5%BC%82%E5%80%BC/9975162
https://blog.youkuaiyun.com/zhongkejingwang/article/details/43053513
7. SNGAN
7.1 SNGAN设计思路
现在我们的目的,是要保证对于每一个位置的x,梯度的模都小于等于1。在神经网络中,将梯度的模限制在一个范围内,抽象地来说就是让产生的函数更平滑一些,最常见的做法便是正则化。SNGAN(频谱归一化GAN)为了让正则化产生更明确地限制,提出了用谱范数标准化神经网络的参数矩阵W,从而让神经网络的梯度被限制在一个范围内。
7.2 频谱范数
我们先以前馈神经网络为一个简单的例子来解释频谱范数(下称谱范数)的作用。(7.2-7.4节是一些相关的理论基础,如果不感兴趣可以直接跳到7.5节)
一个前馈神经网络可以表示为级联计算:![]() 。其中
。其中![]() 代表层数,
代表层数,![]() ;
;![]() 是第
是第![]() 层的输入,
层的输入,![]() 是第
是第![]() 层的输出,
层的输出,![]() 是一个(非线性的)激活函数,
是一个(非线性的)激活函数,![]() 和
和![]() 分别代表
分别代表![]() 层的权重矩阵和偏置向量。现在我们把全体参数的集合记作Θ,Θ=
层的权重矩阵和偏置向量。现在我们把全体参数的集合记作Θ,Θ=![]() ;全体网络层所形成的函数记作
;全体网络层所形成的函数记作![]() ,即有:
,即有:![]() 。给定K组训练数据,
。给定K组训练数据,![]() ,损失函数定义为:
,损失函数定义为:![]() ,通常L被选择为交叉熵或是
,通常L被选择为交叉熵或是![]() 距离,分别用于分类和回归任务。要学习的模型参数是Θ。
距离,分别用于分类和回归任务。要学习的模型参数是Θ。
现在我们开始考虑如何获得对输入的扰动不敏感的模型。 我们的目标是获得一个模型Θ,使得f(x +ξ)-f(x)的模(指的是2-范数,即各个元素的平方和)很小,其中ξ是具有小的模的扰动向量。假设我们选用的激活函数是ReLU或maxout等分段线性函数,在这种情况下,![]() 也是分段线性函数。 因此,如果我们考虑x的小邻域,我们可以将
也是分段线性函数。 因此,如果我们考虑x的小邻域,我们可以将![]() 视为线性函数。 换句话说,我们可以用仿射映射表示它,
视为线性函数。 换句话说,我们可以用仿射映射表示它,![]() ,其中
,其中![]() 是矩阵,
是矩阵,![]() 是向量,它们都取决于Θ和x的值。 然后,对于小扰动ξ,我们有:
是向量,它们都取决于Θ和x的值。 然后,对于小扰动ξ,我们有:
![]()
其中σ![]() 就是
就是![]() 的谱范数的计算式,数学上它等价于计算矩阵
的谱范数的计算式,数学上它等价于计算矩阵![]() 的最大奇异值(奇异值的介绍见7.2节)。矩阵最大奇异值的表达式参见下式:
的最大奇异值(奇异值的介绍见7.2节)。矩阵最大奇异值的表达式参见下式:
![]()
上述论证表明我们应当训练模型参数Θ,使得对于任何x,![]() 的谱范数都很小。 为了进一步研究
的谱范数都很小。 为了进一步研究![]() 的性质,让我们假设每个激活函数
的性质,让我们假设每个激活函数![]() 都是ReLU(该参数可以很容易地推广到其他分段线性函数)。注意,对于给定的向量x,
都是ReLU(该参数可以很容易地推广到其他分段线性函数)。注意,对于给定的向量x,![]() 充当对角矩阵
充当对角矩阵![]() ,其中如果
,其中如果![]() 中的对应元素为正,则对角线中的元素等于1; 否则,它等于零(这是ReLU的定义)。于是,我们可以重写
中的对应元素为正,则对角线中的元素等于1; 否则,它等于零(这是ReLU的定义)。于是,我们可以重写![]() 为下式:
为下式:
![]()
又注意到对于每个![]() ,有σ
,有σ![]() ≤1,所以我们有:
≤1,所以我们有:
![]()
至此我们得出了一个非常重要的结论,为了限制![]() 的谱范数,只需要每个
的谱范数,只需要每个![]() 限制
限制![]() 的谱范数就足够了。这促使我们考虑谱范数正则化,这将在7.3节中描述。
的谱范数就足够了。这促使我们考虑谱范数正则化,这将在7.3节中描述。
7.3* 奇异值与奇异值分解
在介绍频谱范数正则化之前,先简要介绍一下后面会用到的技巧:奇异值分解。奇异值是线性代数中的概念,奇异值分解是矩阵论中一种重要的矩阵分解法,奇异值一般通过奇异值分解定理求得。如果读者了解奇异值的话这一节可以跳过。
奇异值的定义
设A为m*n矩阵,q=min(m,n),A*A的q个非负特征值的算术平方根叫作A的奇异值。
奇异值分解定理
设给定 ![]() ,令
,令 ![]() ,并假设
,并假设 ![]() :
:
(a) 存在酉矩阵 ![]() 与
与 ![]() ,以及一个对角方阵
,以及一个对角方阵
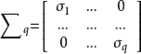
使得![]() 以及
以及 ![]() ,
,
其中 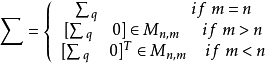
(b) 参数 ![]() 是
是 ![]() 的按照递减次序排列的非零特征值的正的平方根,它们与
的按照递减次序排列的非零特征值的正的平方根,它们与![]() 的按照递减次序排列的非零特征值的正的平方根是相同的。
的按照递减次序排列的非零特征值的正的平方根是相同的。
在奇异值分解定理中,矩阵 ![]() 的对角元素(即纯量
的对角元素(即纯量![]() ,它们是方阵
,它们是方阵 ![]() 的对角元素)称为矩阵A的奇异值。
的对角元素)称为矩阵A的奇异值。
*奇异值分解定理的证明
证明比较复杂,在此不赘述了,推荐一篇博文,感兴趣的读者可以去了解一下:
https://blog.youkuaiyun.com/zhongkejingwang/article/details/43053513。
但是要注意的是,7.3节当中提到了一些概念,其中左奇异向量指的是![]() 的特征向量,右奇异向量指的是
的特征向量,右奇异向量指的是![]() 的特征向量。
的特征向量。
7.4 频谱范数正则化
频谱范数正则化方法是17年5月提出来的,虽然最终的SNGAN没有完全采用这一方法,但是它借鉴了这个方法非常重要的思想。
为了约束每个权重矩阵的频谱范数![]() ,我们考虑以下经验风险最小化问题:
,我们考虑以下经验风险最小化问题:
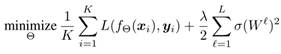
其中λ∈![]() 是正则化因子,第二项被称为谱范数正则项,它降低了权重矩阵的谱准则。
是正则化因子,第二项被称为谱范数正则项,它降低了权重矩阵的谱准则。
在执行标准梯度下降时,我们需要计算谱范数正则项的梯度。为此,让我们考虑对于一个特定![]() 的梯度σ(
的梯度σ(![]() /2,其中
/2,其中![]() 。 设
。 设![]() =σ(
=σ(![]() 和
和![]() 分别是第一和第二奇异值。 如果
分别是第一和第二奇异值。 如果![]() >
>![]() ,则σ(
,则σ(![]() /2的梯度为
/2的梯度为![]() ,其中,
,其中,![]() 和
和![]() 分别是第一个左奇异向量和第一个右奇异向量。 如果
分别是第一个左奇异向量和第一个右奇异向量。 如果![]() =
=![]() ,则σ(
,则σ(![]() /2是不可微的。 然而,出于实际目的,我们可以假设这种情况从未发生,因为实际训练中的数值误差会让
/2是不可微的。 然而,出于实际目的,我们可以假设这种情况从未发生,因为实际训练中的数值误差会让![]() 和
和![]() 不可能完全相等。
不可能完全相等。
由于计算![]() ,
,![]() 和
和![]() 在计算上是昂贵的,我们使用功率迭代方法来近似它们。从随机初始化的v开始(开始于
在计算上是昂贵的,我们使用功率迭代方法来近似它们。从随机初始化的v开始(开始于![]() 层),我们迭代地执行以下过程足够次数:
层),我们迭代地执行以下过程足够次数:
![]()
最终我们得到了使用频谱范数正则项的SGD算法如下:

值得注意的是,为了最大化![]() ,
,![]() 和
和![]() ,在SGD的下一次迭代开始时,我们可以用
,在SGD的下一次迭代开始时,我们可以用![]() 代替第2步中的初始向量v。然后在第7步中右方的标注是,paper作者在实验中发现,只进行一次迭代就能够获得足够好的近似值。文章中还提到对于含有卷积的神经网络架构,我们需要将参数对齐为b×a
代替第2步中的初始向量v。然后在第7步中右方的标注是,paper作者在实验中发现,只进行一次迭代就能够获得足够好的近似值。文章中还提到对于含有卷积的神经网络架构,我们需要将参数对齐为b×a![]() 的矩阵,再去计算该矩阵的谱范数并添加到正则项中。
的矩阵,再去计算该矩阵的谱范数并添加到正则项中。
综上,频谱范数正则化看起来非常复杂,但是它的实际做法,可以简单地理解为,把传统GANs中的loss函数:
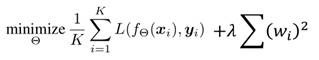
其中的正则项替换成了谱范数:
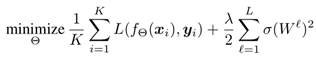
并且谱范数的计算利用了功率迭代的方法去近似。
7.5 SNGAN的实现
之前我们说到,对于GANs最重要的目的是实现D的1-lipschitz限制,频谱范数正则化固然有效,但是它不能保证把![]() 的梯度限制在一个确定的范围内,真正解决了这一问题的,是直到18年2月才被提出的SNGAN。SNGAN基于spectral normalization的思想,通过对W矩阵归一化的方式,真正将
的梯度限制在一个确定的范围内,真正解决了这一问题的,是直到18年2月才被提出的SNGAN。SNGAN基于spectral normalization的思想,通过对W矩阵归一化的方式,真正将![]() 的梯度控制在了小于或等于1的范围内。
的梯度控制在了小于或等于1的范围内。
我们先来证明,只要将每一层![]() 的谱范数都限制为1,最终得到的
的谱范数都限制为1,最终得到的![]() 函数就会满足1-lipschitz限制。
函数就会满足1-lipschitz限制。
对于一个线性层函数g(h)=Wh,我们可以计算出它的lipschitz范式:
![]()
如果激活层函数的lipschitz范式![]() =1(比如ReLU),我们就有如下不等式:
=1(比如ReLU),我们就有如下不等式:
![]()
其中○表示复合函数。我们利用上面的不等式,就能够得到![]() 的lipschitz范式的限制式:
的lipschitz范式的限制式:
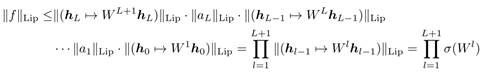
于是现在,我们只需要保证![]() 恒等于1,就能够让
恒等于1,就能够让![]() 函数满足1-lipschitz限制。做法非常简单,只需要将W矩阵归一化即可:
函数满足1-lipschitz限制。做法非常简单,只需要将W矩阵归一化即可:
![]()
至此,SNGAN通过将W矩阵归一为谱范数恒等于1的式子,进而控制![]() 的梯度恒小于等于1,最终实现了对D的1-lipschitz限制,最后我们给出SNGAN中的梯度下降算法:
的梯度恒小于等于1,最终实现了对D的1-lipschitz限制,最后我们给出SNGAN中的梯度下降算法:

可以看出,与传统的SGD相比,带有谱归一化的SGD做的额外处理就是对W矩阵做的归一化处理:
![]()





 本文深入解析SNGAN(频谱归一化生成对抗网络)的设计思路与实现原理,阐述其如何通过频谱范数正则化及W矩阵归一化控制梯度,实现对生成模型的稳定训练。
本文深入解析SNGAN(频谱归一化生成对抗网络)的设计思路与实现原理,阐述其如何通过频谱范数正则化及W矩阵归一化控制梯度,实现对生成模型的稳定训练。
















 1500
1500

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








