找到字符串中所有字母异位词P438

原文链接

方法一:暴力枚举 + 排序比较
截取每一个符合p长度的字串进行比较

public static boolean compare(String str1, char[] c2) {
    char[] c1 = str1.toCharArray(); // 将字符串转换为字符数组
    Arrays.sort(c1); // 对字符数组进行排序

    // 比较两个排序后的字符数组是否相等
    return Arrays.equals(c1, c2);
}

public static List<Integer> findAnagrams(String s, String p) {
    List<Integer> res = new ArrayList<>(); // 存储找到的起始索引
    char[] c2 = p.toCharArray();
    Arrays.sort(c2); // 对 p 进行排序，后续用于比较
    int n = s.length(); // s 的长度
    int m = p.length(); // p 的长度

    // 遍历 s 的所有可能子串，检查是否为 p 的变位词
    for (int i = 0; i <= n - m; i++) {
        String sub = s.substring(i, i + m); // 取长度为 m 的子串
        if (compare(sub, c2)) { // 判断是否为变位词
            res.add(i); // 记录起始索引
        }
    }
    return res;
}

能成功，但是执行速度比较慢

方法2:滑动窗口 + 计数数组
在方法1的基础上优化，采用了滑动窗口技术和频率数组，通过维护当前窗口内的字符频率，避免了排序操作。每次滑动时，只更新窗口内字符的计数
使用滑动窗口的方式遍历字符串 s，窗口大小为 p 的长度。

1.使用两个频率数组 freqS 和 freqP，分别记录 s 中当前窗口和 p 中字符的频率。

2.初始化时，统计 p 中每个字符的出现次数。

3.遍历字符串 s，滑动窗口：

 3.1增加右侧新字符的计数。

 3.2窗口等于p字符的长度时，每次都会移除左侧字符

4.在每次滑动时，比较当前窗口的频率数组 freqS 和 freqP 是否相同，若相同，则该窗口是 p 的变位词。

过程如下:
1、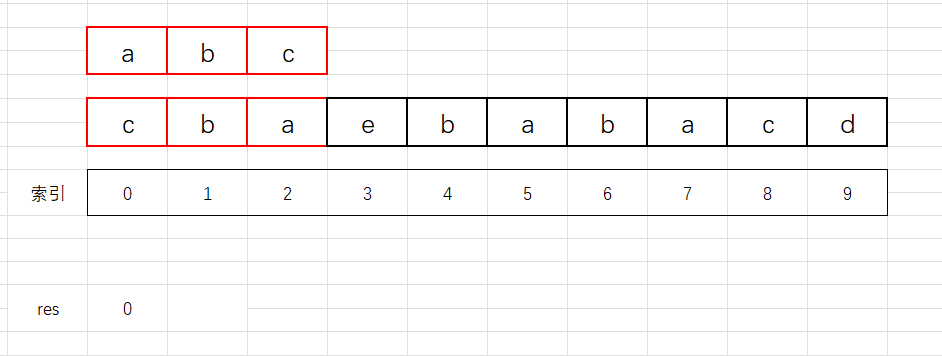

2、

3、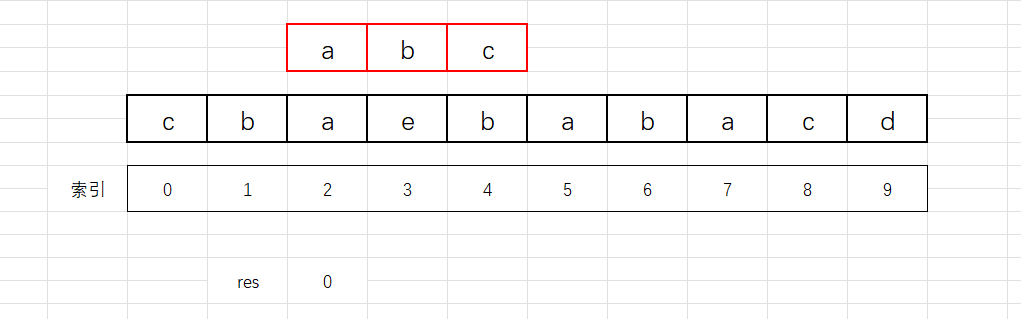

4、

5、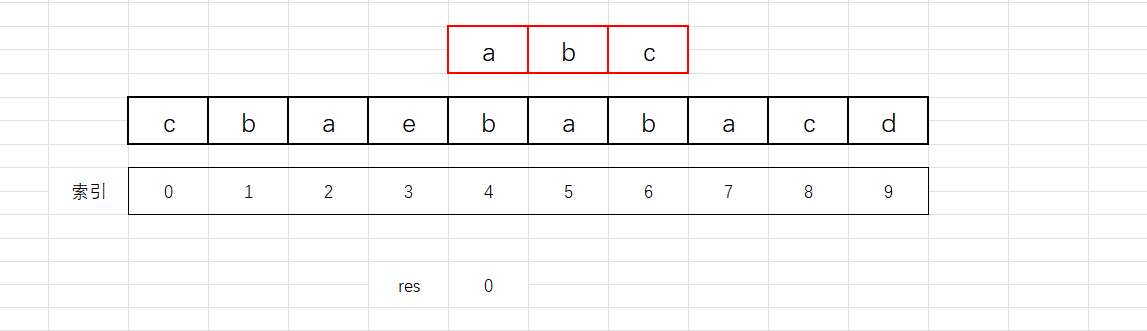

6、

7、

8、

public static List<Integer> findAnagrams(String s, String p) {
    List<Integer> result = new ArrayList<>(); // 存储找到的起始索引
        int[] freqS = new int[26]; // 记录当前窗口内字符出现的频率
        int[] freqP = new int[26]; // 记录字符串 p 中字符出现的频率

        // 统计字符串 p 中每个字符的出现次数
        for (char c : p.toCharArray()) {
            freqP[c - 'a']++;
        }

        // 滑动窗口遍历字符串 s
        for (int i = 0; i < s.length(); i++) {
            freqS[s.charAt(i) - 'a']++; // 增加当前字符的计数
            int leftIndex = i - p.length() + 1; // 计算窗口左侧的索引
            if (leftIndex < 0) continue; // 确保窗口大小等于 p 的长度
            // 判断当前窗口是否为 p 的变位词
            if (Arrays.equals(freqP, freqS)) {
                result.add(leftIndex); // 记录起始索引
            }
            // 移除窗口最左侧的字符，保持窗口大小不变
            freqS[s.charAt(leftIndex) - 'a']--;
        }

        return result;

复杂度分析

暴力 + 排序解法：
枚举 s 的 O(n - m + 1) 个子串，每个子串排序 O(m log m)
总时间复杂度：O(n m log m)（较慢）
空间复杂度：O(m + n)

滑动窗口 + 计数数组优化解法：
初始化 p 的计数 O(m)，然后滑动窗口遍历 O(n)，
总时间复杂度：O(n + m)（更快）
空间复杂度：O(26) = O(1)（常数级）