UPC 组队训练 Network Report（Floyd）

问题 D: Network Report
时间限制: 1 Sec 内存限制: 128 MB
提交: 139 解决: 58
[提交] [状态] [讨论版] [命题人:admin]
题目描述

For time efficiency, data transmission is often done along the shortest path (with minimum number of hops) between network nodes. In the network graph (undirected and unweighted) below, the length of the shortest path from node 0 to node 2 is 2, and the length of the shortest path from node 0 to node 4 is 3. For a network graph with n nodes, we want to find all-pairs shortest paths, and provide a summary report on how many shortest paths are there for each length (from 1 to the maximal length). That is, this summary report should contain the total number of shortest paths of length 1, the total number of shortest paths of length 2, and so on and so forth.
Note that if multiple shortest paths from node i to node j (i ≠ j) exist, they should collectively count as one. For example, though there are two shortest paths from node 0 to node 4, only one path is counted. Please write a program to output the above summary report from an input connected graph.

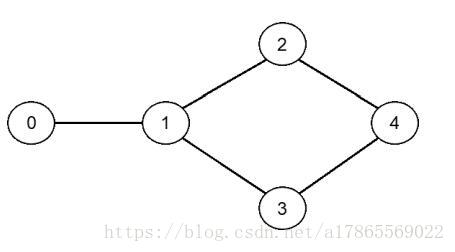
输入

The input contains multiple instances of an undirected and unweighted connected graph (not multigraph). For each instance, the first line contains a single integer n. The second line contains a single integer e, denoting the number of edges in the graph. For the next e lines, each line contains two integers i, j, denoting that there is an edge connecting node i and node j. There is a 0 on a single line following the last test instance. There are at most 10 test instances.

输出

For each instance, there are several lines of output pending on the input. Each line of output consists of two integer numbers separated by a single space, where the first number is the path length and the second number is the total number of shortest paths of the corresponding length. The output should display the results from length 1 to the maximal length in the graph incrementally.

样例输入

3
3
0 1
1 2
2 0
5
5
0 1
1 2
1 3
2 4
3 4
0

样例输出

1 6
1 10
2 8
3 2

提示

1. 2 ≤ n ≤ 200, nodes are numbered as 0, 1, 2, … , n − 1.
2. Any counting number is within the range of integer.
   题意：有N个点，每两个直接相连的点之间的权值看做1，遍历这个图，统计从长度为1到长度为max 的路个有几条。
   思路：Floyd算法。

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
int Map[205][205];
int cnt[205];
int n,e,a,b;
int main()
{
    while(scanf("%d",&n) &&n!=0)
    {
        memset(Map,INF,sizeof(Map));
        memset(cnt,0,sizeof(cnt));
        for(int i=0;i<n;i++)
            Map[i][i] = 0;
        scanf("%d",&e);
        for(int i=0;i<e;i++)
        {
            scanf("%d %d",&a,&b);
            Map[a][b]=Map[b][a]=1;
        }
        for(int k=0;k<n;k++)
        {
            for(int i=0;i<n;i++)
            {
                for(int j=0;j<n;j++)
                {
                    Map[i][j]=min(Map[i][j],Map[i][k]+Map[k][j]);
                }
            }
        }
        for(int i=0;i<n;i++)
        {
             for(int j=0;j<n;j++)
             {
                 if(Map[i][j]!=INF)
                    cnt[Map[i][j]]++;
             }
        }
        for(int i=1;i<=n-1;i++)
        {
            if(cnt[i]!=0)
                printf("%d %d\n",i,cnt[i]);
        }
    }
    return 0;
}