数据结构上机实现——关键路径

前言

首先在保证没有环路的基础上，任选一个顶点，从它开始，计算每一个顶点的最早最晚时刻，如果最晚时刻减去当前工序所持续的时间（权值）和最早时刻相等，则该点为关键工序，各关键工序顺次连接就构成了关键路径。同样，注释已经很详细了，原理不做深究，请自行复习。

---

注：本文的实验案例都是清华大学严蔚敏老师数据结构视频中所讲解的案例，所以本类的文章是十分适合大家对课上知识加深认识的。测试案例和源代码将会在文末给出。

---

算法

本算法的存储结构为邻接矩阵，类型声明如下：

typedef struct _graph {
	int matrix[MAX][MAX];//二维数组表示的矩阵
	char vexs[MAX];//顶点集
	int vexnum;//顶点个数
	int edgnum;//边的个数
}Graph, *pGraph;//邻接矩阵的存储结构，用pGraph指针指向

下面是算法本体

void critical(Graph*gra) {
	int n = gra->vexnum;
	vector<int> topo(n);
	if (!topological(gra, topo)) return;//说明图中有环路
	vector<int> ve(n);
	vector<int> vl(n, INF);
	//从拓扑集合中依次选取顶点，进行ve的统计
	for (int i = 0; i < n; i++) {
		int k = topo[i];//用k记录当前的节点
		//探索从k到j的路径
		for (int j = 0; j < n; j++) {
			if (gra->matrix[k][j] != INF && gra->matrix[k][j] != 0) {//必须存在路径，不能包括自身
				if (ve[k] + gra->matrix[k][j] > ve[j]) {//选择较大的
					ve[j] = ve[k] + gra->matrix[k][j];
				}
			}
		}
	}
	//从拓扑集合中倒着选取顶点，进行vl的统计
	vl[n - 1] = ve[n - 1];//最后一个工序的ve和vl是相等的
	for (int i = n - 1; i >= 0; i--) {//注意是反过来的
		int k = topo[i];
		//探索从j到k的路径
		for (int j = 0; j < n; j++) {
			if (gra->matrix[j][k] != INF && gra->matrix[j][k] != 0) {
				if (vl[k]-gra->matrix[j][k] < vl[j]) {//选择较小的
					vl[j] = vl[k] - gra->matrix[j][k];
				}
			}
		}
	}
	//每道工序最早最迟判断
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (gra->matrix[i][j] != INF && gra->matrix[i][j] != 0) {//保证有路径
				if (ve[i] == vl[j] - gra->matrix[i][j]) {//最早最迟相同
					cout << gra->vexs[i] << " " << gra->vexs[j] << endl;
				}
			}
		}
	}
}

上机须知

严姥姥给的例子

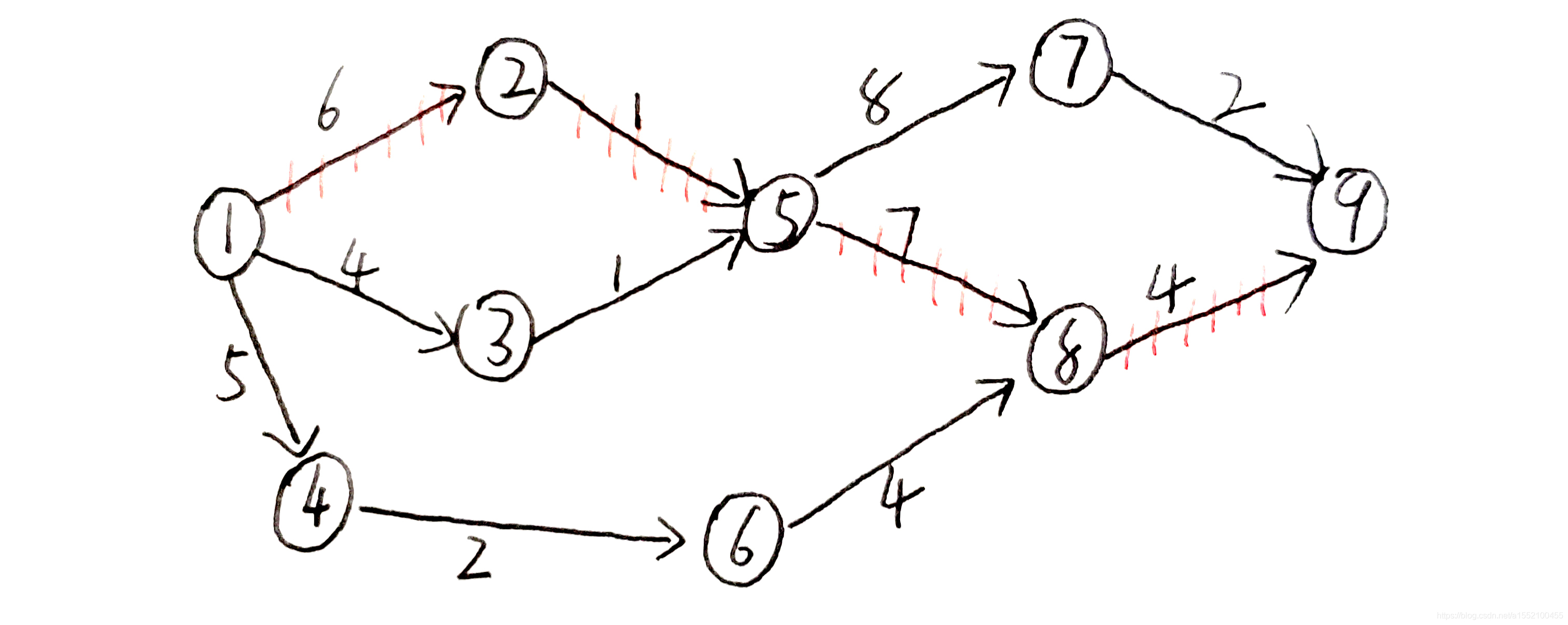
 对应的邻接矩阵
0 6 4 5 * * * * *
* 0 * * 1 * * * *
* * 0 * 1 * * * *
* * * 0 * 2 * * *
* * * * 0 * 8 7 *
* * * * * 0 * 4 *
* * * * * * 0 * 2
* * * * * * * 0 4
* * * * * * * * 0

在我给出的测试源码里需要输入以下内容，直接粘贴就可以

9
11
1
2
3
4
5
6
7
8
9
1 2 6
1 3 4
1 4 5
2 5 1
3 5 1
4 6 2
5 7 8
5 8 7
6 8 4
7 9 2
8 9 4

源码地址：点击这里