CodeforcesRound#549(Div. 2)(A-D题解)-优快云博客

http://codeforces.com/problemset/problem/1143/A

题意：给你一串01代表n个按钮（0是一种，1是一种），如果同种按钮都按过了，你就能逃生，但你必须从头开始按按钮。问你逃生前按下的最后一个按钮标号。

思路：从最后一个开始，如果有一个按钮跟最后一个按钮不同，输出标号即可。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int a[200005];
 5 int main() {
 6     int n;
 7     cin >> n;
 8     for(int i = 1;i <= n;i ++){
 9         cin >> a[i];
10     }
11     int t = a[n];
12     for(int i = n;i >= 1;i --){
13         if(a[i] != t){
14             cout << i << endl;
15             break;
16         }
17     }
18 
19     return 0;
20 }

http://codeforces.com/problemset/problem/1143/B

题意：求出1到n的所有数的最大数位积（每一位相乘的结果）。

思路：可以模拟来求，代码量可能会大一点，但是此处可用记忆化搜索。

　　　令表达式 Dgt(n) 代表 n 的数位积：

　　　　如果想让 Dgt(n) 最大，那么必须满足以下两点：

　　　　　　1、Dgt(n/10) * (n%10) 最大；

　　　　　　2、Dgt(n/10 - 1) * 9 最大。（比如258，那么某个接近他的理想状态应该是249，968则是959，因为要保证9的数量）

　　　　所以只需要对上述两种情况求max值。

　　　这个代码竟然卡了我好久，看来是菜了不少啊。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int solve(int x){
 5     if(x == 0){return 1;}
 6     if(x < 10){return x;}
 7     int t1 = (x % 10) * solve(x / 10);
 8     int t2 = 9 * solve((x / 10) - 1);
 9     return max(t1,t2);
10 }
11 
12 
13 int main(){
14     int n;
15     cin >> n;
16     cout << solve(n) << endl;
17 
18     return 0;
19 }

http://codeforces.com/problemset/problem/1143/C

题意：给一个有根树，如果一个点被标记了1，并且这个点所有儿子也都是1，那么这个点可以被删去，并且这个点的所有儿子会连接到它的父亲身上。

　　　如果有点能删，那么就删掉，如果同时出现多个点可删，那么删掉最小标号的点。

　　　一直删到没有任何点可以删去，那么就结束。

　　　按顺序输出删点过程，初始则是无点可删树，则输出-1。

思路：仔细想想。。。这个破树在删点过程中完全不会出现逆序。一定是先删序号小的点，再删序号大的点。

　　　暴力跑一遍即可。

　　　这破玩应我也证明了一会。。。好像傻。。。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 vector<int> V[100005];
 5 int R[100005];
 6 int C[100005];
 7 int main(){
 8     int n;
 9     cin >> n;
10     memset(R,0,sizeof(R));
11     memset(C,0,sizeof(C));
12     for(int i = 1;i <= n;i ++){
13         int t1,t2;
14         cin >> t1 >> t2;
15         if(t1 != -1){V[t1].push_back(i);}
16         R[i] = t2;
17     }
18     for(int i = 1;i <= n;i ++){
19         int CD = 1;
20         for(int j = 0;j < V[i].size();j ++){
21             if(R[V[i][j]] == 0){CD = 0;break;}
22         }
23         C[i] = CD;
24     }
25     int f = 1;
26     for(int i = 1;i <= n;i ++){
27         if(C[i] && R[i]){cout << i << " ";f = 0;}
28     }
29     if(f){cout << "-1" << endl;}
30 
31     return 0;
32 }

http://codeforces.com/problemset/problem/1142/A

题意：题面十分缺德，大概翻译一下：

　　　有一个环，大小是 n*k （n 和 k 已知），有一个人在未知起点 S 开始走，未知步长为 L。

　　　在这个环上，有k个饭店，分别在 1，(1+k)，(1+2k)......

　　经过未知步数后这个人会走回 S，此时结束。

　　　你还知道两个常数 a 和 b。a 代表你的初始位置和初始位置最近的饭店距离，b 代表你走过一步之后的位置和当前位置最近的饭店距离。

　　　求最小可能步数以及最大可能步数。

思路：黑色点是饭店，白色点没有东西，绿色点是起点，红色点是从起点走过一步之后的位置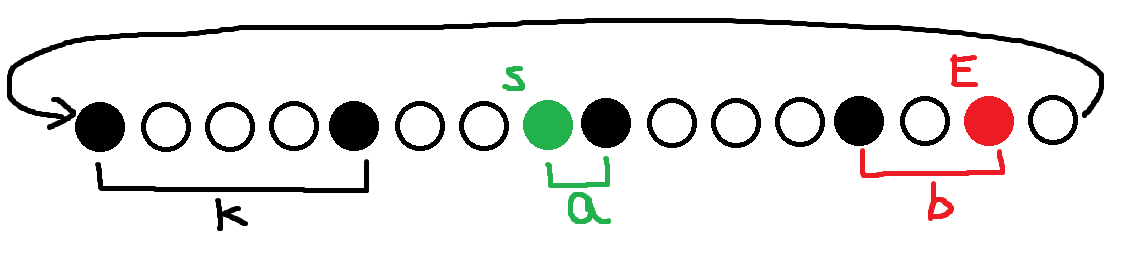

　　　设步行次数为 ans ；n，a，b，L，k 均为题意所给含义，则有：

　　　　ans * L = n * k * x (x为某个常数，未知量)；

　　　　(±a ±b) + y * k = L (y为某个常数，未知量，(±a ±b)代表4个不同的表达式，所有情况都取到)；

　　　　gcd(ans,x) == 1。

　　　　可根据L联立两个等式：(n * k * x) / ans = (±a ±b) - y * k 。

　　　　这样我们发现，右侧的部分是可以使用 y 进行枚举的，而且 y 的极值不会超过 n 。

　　　　那么 L 就等于 (±a ±b) - i * k，(此时 i 为枚举值)

　　　　整理：L * ans = (n * k) * x 。

　　　　此时，只有 x 和 ans 是未知的了，但是前面给出了 gcd(ans,x) == 1。

　　　　那么我们可以让 G = gcd(n * k,L)，再将 L 和 n * k 分别除以 G 。

　　　　这样出现了 gcd(n * k / G,L / G) == 1 。

　　　　那么就形成了等式两边出现两对互质的数，那么一定存在 ans = n * k / G 。

　　　所以这道题，只需要进行枚举四种情况的 1 到 n 即可。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 long long maxx,minn;
 5 long long n,k,a,b;
 6 
 7 void solve(long long z){
 8     for(long long i = 1;i <= n;i ++){
 9         long long L = k * i + z;
10         long long G = __gcd(n * k,L);
11         long long res = n * k / G;
12         if(res > 0){
13             maxx = max(maxx,res);
14             minn = min(minn,res);
15             //cout << minn << " " << maxx << endl;
16         }
17     }
18 }
19 
20 int main()
21 {
22     maxx = -1;
23     minn = 1000000000000000000;
24     cin >> n >> k >> a >> b;
25         solve(a + b);
26     solve(a - b);
27     solve(b - a);
28     solve(0LL - a - b);
29     cout << minn << " " << maxx << endl;
30 
31     return 0;
32 }