hot 100道 链表-堆 解题心得（二）

七、链表

1、环形链表 II

1）关键解题思路
无非就是定义一个fast = fast.next.next slow = slow.next 如果有环它们最终一定会在某个地方相见即为：fast = slow；

2）代码

public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode slow = head;
        ListNode fast = head;
        while(fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
              ListNode  pre = head;
                while (pre != slow) {
                    pre = pre.next;
                    slow = slow.next;
                }
                return pre;
            }
        }
        return null;
    }

2、两数相加

1）关键解题思路
定义一个虚拟头节点便于后续操作，并定义一个 carry 作为进位标志，然后进行遍历，其他看代码自行可理解

2）代码

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode head = new ListNode(-1);
        ListNode cur = head;
  
        int carry = 0;
          int sum  = 0;
          int cur1Val = 0;
           int cur2Val = 0;
        while(l1 !=null || l2 !=null){
             cur1Val = l1 == null?0: l1.val;
            cur2Val = l2 == null?0: l2.val;
            // carry上一次计算的进位
            sum = cur1Val+ cur2Val + carry;
            carry = sum/10;
            sum = sum%10;
            ListNode newNode = new ListNode(sum);
            cur.next = newNode;
            cur =  newNode;
            l1 = l1 == null ?null:l1.next;
            l2= l2 == null? null:l2.next;
        }
        if(carry == 1){
             ListNode newNode = new ListNode(1);
             cur.next = newNode;
             cur = newNode;
        }
        return head.next;
    }

3、删除链表的倒数第 N 个结点

1）关键解题思路
解题有两种方法：

1. 就是先遍历链表得到链表的总长度 size ，然后再遍历 size -n 遍即可找到所需节点。
2. 定义一个虚拟头节点，并定义fast ，slow 其中fast先移动n步，然后fast slow 同时移动，等到 fast.next = null 时候 slow 即为删除节点的前一个节点，最后进行后续操作即可。

2）代码

  // 2.快慢指针
     public ListNode removeNthFromEnd(ListNode head, int n) {
        // 定义虚拟头节点 双指针解法 得连上头节点
        // 为何定义虚拟头节点，便利如果删除的是head头节点，可以找到前一点的位置删除
        ListNode preHead = new ListNode(-1, head);
        ListNode slow = preHead;
        // 定义快指针
        ListNode fast = preHead;
        while (n-- != 0 && fast != null) {
            fast = fast.next;
        }
        while (fast.next != null) {
            fast = fast.next;
            slow = slow.next;
        }
        // slow代表的是前一个要删除头节点的
        slow.next = slow.next.next;
        return preHead.next;
    }

4、两两交换链表中的节点

1）关键思路
为了方便定义一个虚拟头节点，然后在虚拟头节点之上进行遍历，然后保存前三个节点的地址，为了后续交换使用，等到交换结束后继续进行下一轮交换，此时下一轮交换 cur 转移到了下两个节点进行交互的前一个节点，如果此时只有一个或者没有节点了直接停止交换,
即为：cur.next != null && cur.next.next != null 条件

2）代码

public ListNode swapPairs(ListNode head) {
        // 定义虚拟头节点 （关键点）
        ListNode dummy = new ListNode(-1, head);
        ListNode cur = dummy;
        while (cur.next != null && cur.next.next != null) {
            ListNode l1 = cur.next;
            ListNode l2 = l1.next;
            ListNode l3 = l2.next;
            cur.next = l2;
            l2.next = l1;
            l1.next = l3;
            cur = l1;
        }
        return dummy.next;
    }

5、K 个一组翻转链表

1）关键解题思路
2）代码

1. 错误代码 reverseNode（）

public ListNode reverseKGroup(ListNode head, int k) {
        // 定义虚拟头节点 （关键点）
        int n = k;
        ListNode dummy = new ListNode(-1, head);
        ListNode cur = dummy;
        ListNode start = dummy.next;
        ListNode end = dummy.next;
        while (true) {
            n = k;
            while (--n != 0 && end != null) {
                end = end.next;
            }
            if (end == null) break;
            // 保存下一个 start 节点，用于连接反转后的链
            ListNode nextStart = end.next;
            ListNode nodeHead = reverseNode(start,end);

            // 连接反转后的部分
            cur.next = nodeHead;
            start.next = nextStart;

            // 更新cur 和start 准备下一轮反转
            cur = start;
            start = start.next;
            end = start;
        }
        return dummy.next;
    }


    private ListNode reverseNode(ListNode start, ListNode end) {
        ListNode pre = null;
        ListNode curr = start;
        while (curr != end.next) {
            ListNode temp = curr.next;
            curr.next = pre;
            pre = curr;
            curr = temp;
        }
        return pre;
    }

分析错误代码
需要执行的流程图

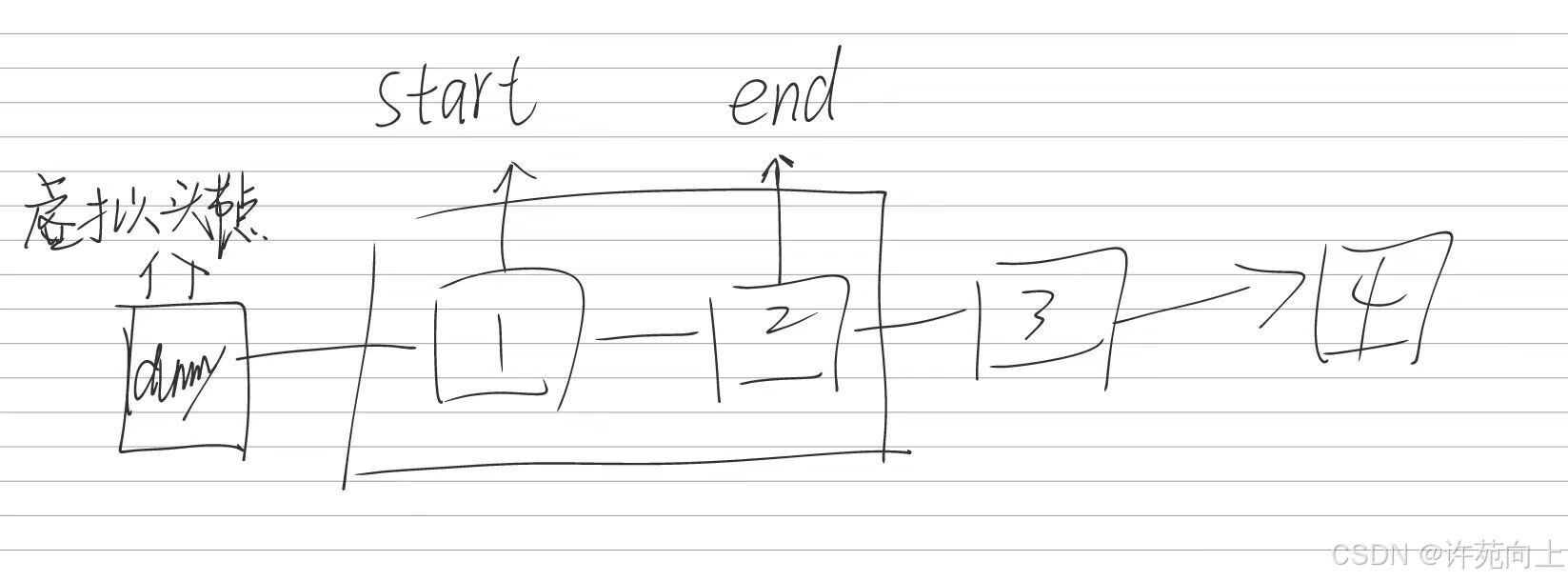
curr != end.next 当 cur = end时候的流程图

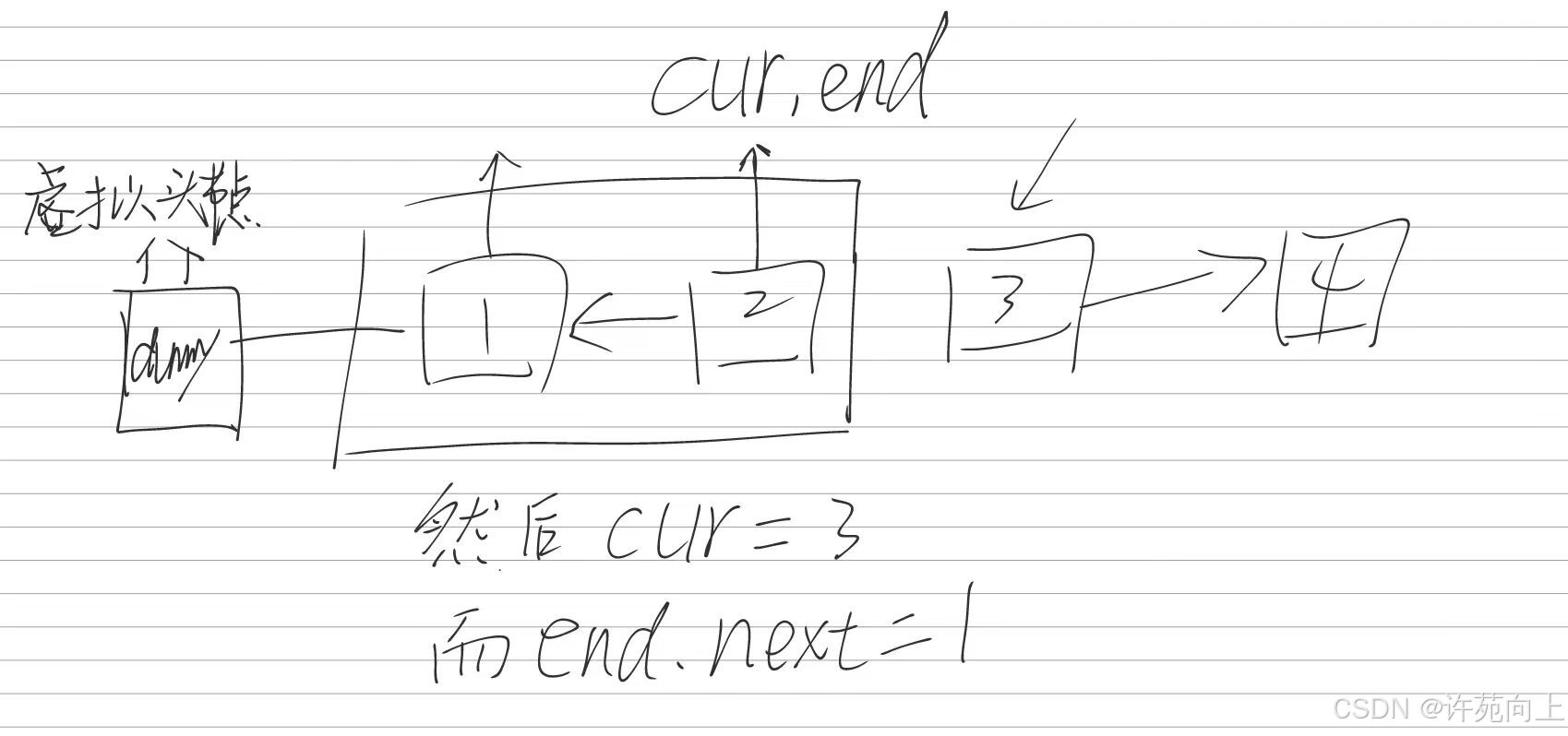
然后继续执行这段代码

			curr.next = pre;
            pre = curr;
            curr = temp;

cur -> 3 ，end.next -> 2然后本应该是跳循环时候，但是这样根本不会跳出来，也就导致了错误。

总结错误原因就是：没有断开左右两边的连接，且没有注意到只要你传递指针地址进来，其实也会相应改变链表本身的结构，但是不会影响原来的值。例如传递start 进去，reverseNode方法改变了start值，但是对于外部的start值还是传递进方法之前的值，不会受方法里面的改变而改变。

    ListNode nodeHead = reverseNode(start,end);

            // 连接反转后的部分
            cur.next = nodeHead;
            start.next = nextStart;
            
 private static ListNode  reverseNode(ListNode start, ListNode end) {
        ListNode pre = null;
        int n = 2;
        while (n-- !=0) {
            ListNode temp = start.next;
            start.next = pre;
            pre = start;
            start = temp;
        }
        return pre;
    }

2. 正确代码

 public ListNode reverseKGroup(ListNode head, int k) {
        // 定义虚拟头节点 （关键点）
        int n = k;
        ListNode dummy = new ListNode(-1, head);
        ListNode cur = dummy;
        ListNode start = dummy.next;
        ListNode end = dummy.next;
        while (true) {
            n = k;
            while (--n != 0 && end != null) {
                end = end.next;
            }
            if (end == null) break;
            // 保存下一次连接的地方
            ListNode next = end.next;
               // 断裂前后
            cur.next = null;
            end.next = null;
            ListNode nodeHead = reverseNode(start);
            cur.next = nodeHead;
            // 连接下一层
            start.next = next;
            cur = start;
            start = start.next;
            end = start;
          
        }
        return dummy.next;
    }

    
    private ListNode reverseNode(ListNode start) {
        ListNode pre = null;
        while (start != null) {
            ListNode temp = start.next;
            start.next = pre;
            pre = start;
            start = temp;
        }
        return pre;
    }

正确分析：
将需要分组的链表进行前后断裂 = null ，然后在反转链表 star = null时候进行退出即可，而不能使用 start != end.next 因为当start == end时候 然后修改start.next = pre 其实同样的也修改了end.next = pre，因为它们指向同一个指针，会造成本应该退出的循环没有退出。

6、随机链表的复制

1）关键思路
最关键思路无非就是内存换时间，使用hm存放遍历每个cur对于的newNode节点，后续可以直接使用。
2）代码

   public Node copyRandomList(Node head) {
        Node cur = head;
        // 使用cur：键  newNode:值
        HashMap<Node,Node> hm = new HashMap();
        while(cur != null){
            hm.put(cur, new Node(cur.val));
            cur = cur.next;
        }
        cur = head;
        while(cur != null){
            hm.get(cur).next = hm.get(cur.next);
            hm.get(cur).random = hm.get(cur.random);
            cur = cur.next;
        }
        return hm.get(head);
    }

7、排序链表

1）解题思路
有点类似于数组排序算法，但是得从中挑选出来合适的排序方法也适用于链表排序，那么可以使用归并，因为归并是可以断开链表的，故而可以使用归并进行不断划分然后合并
2）代码

 public ListNode sortList(ListNode head) {
        if (head == null || head.next == null) return head;
        ListNode slow = head;
        ListNode fast = head.next;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        ListNode temp = slow.next;
        // 断开链表连接
        slow.next = null;
      ListNode left =   sortList(head);
        ListNode right =  sortList(temp);
        ListNode res =  mergeNode(left, right);
        return res;
    }

    private ListNode mergeNode(ListNode head, ListNode temp) {
        ListNode dummy = new ListNode(-1);
        ListNode cur = dummy;
        while (head != null && temp != null) {
            if (head.val >= temp.val) {
                cur.next = temp;
                cur = temp;
                temp = temp.next;
            }   else if (head.val < temp.val) {
                cur.next = head;
                cur = head;
                head = head.next;
            }
        }
       cur.next =  head == null ? temp : head;
        return dummy.next;
    }

8、合并K个升序链表

1）解题关键思路
当想不到其他方法时候，可以想想使用存储空间，利用空间换时间，定义一个优先列表，里面始终维护着一个升序的节点列表

2）代码

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        Queue<ListNode> pq = new PriorityQueue<>((v1, v2) -> v1.val - v2.val);
        // 依次把头节点放进去先
        for (ListNode node: lists) {
            if (node != null) {
                pq.offer(node);
            }
        }

        ListNode dummyHead = new ListNode(0);
        ListNode tail = dummyHead;
        while (!pq.isEmpty()) {
            ListNode minNode = pq.poll();
            tail.next = minNode;
            tail = minNode;
            if (minNode.next != null) {
                pq.offer(minNode.next);
            }
        }

        return dummyHead.next;
    }
}

3）分析

• 利用小顶堆进行排序。始终维护着一个升序的队列

9、LRU缓存

代码：

class LRUCache {
     // 第一个节点代表是最近使用的节点
  static class Node{
        int key;
        int val;
        Node next ,prev;
        public Node(int key, int val) {
            this.key = key;
            this.val = val;
        }
    }

    private int capacity;
    HashMap<Integer, Node> hm = new HashMap<>();
    Node dummy = new Node(-1,-1);
    public LRUCache(int capacity) {
        this.capacity = capacity;
        dummy.next = dummy;
        dummy.prev = dummy;
    }


    public int get(int key) {
        Node node = getNode(key);
        if (node == null) return -1;
        return node.val;
    }

    public void put(int key, int value) {
        Node node = getNode(key);
        if (node != null) {
            node.val = value;
            return ;
        }
              node = new Node(key, value);
            hm.put(key, node);
            pushHead(node);
            
           if (hm.size() > capacity) {
            hm.remove(dummy.prev.key);
              removeNode(dummy.prev);
           }
    }

    public void  removeNode(Node node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    public Node getNode(int key) {
        if (!hm.containsKey(key)) return null;
        Node node = hm.get(key);
        removeNode(node);
        pushHead(node);
        return node;
    }

    public void pushHead(Node node) {
        node.next = dummy.next;
        dummy.next.prev = node;
        node.prev = dummy;
        dummy.next = node;
    }
}

注意在put过程中 ，以下这段代码 -> 顺序是不能够变换的，否则会出现空指针异常。

if (hm.size() > capacity) {
            hm.remove(dummy.prev.key); // 顺序是不能够变换的，否则会出现空指针异常
              removeNode(dummy.prev);// 
           }

原因如下： removeNode(dummy.prev);先进行的话，链表此时已经将最后一个节点删除了，导致最后一个节点丢失，此时 hm 哈希表里面还没有将最后一个节点删除，虽然使用了dummy.prev,但实际上已经不是之前的那个末尾节点了

八、二叉树

解题关键

在于理解递归含义以及遍历顺序。

什么叫递归？递归含义是什么？为什么理解它成为解题二叉树内容的关键？

常说递归，递归，什么叫递归？递归就是原问题和子问题类似，都是同样的解法，将原问题拆分成多个相同的子问题，然后通过递归解决。

1、二叉树的直径

1）本题解答关键概念：

链：从子树中的叶子节点到当前节点的路径。把最长链的长度，作为 dfs 的返回值。根据这一定义，空节点的链长是 −1，叶子节点的链长是 0。
直径：等价于由两条（或者一条）链拼成的路径。我们枚举每个 node，假设直径在这里**「拐弯」**，也就是计算由左右两条从下面的叶子节点到 node 的链的节点值之和，去更新答案的最大值。
求最大直径：一定是叶子节点到另外一个叶子节点，故而必须先求左，右最大直径，然后与根相加得出最大结果。
确定遍历顺序最为重要，本题使用的是后序遍历。

2）算法如下图所示

3）代码结果

 int ans;
    public int diameterOfBinaryTree(TreeNode root) {
        ans = 1;
        depth(root);
        return ans ;
    }
    public int depth(TreeNode node) {
        if (node == null) {
            return - 1; // 访问到空节点了，返回-1
        }
        int L = depth(node.left); // 左子树的最长链
        int R = depth(node.right); // 右子树的最长链
        ans = Math.max(ans, L+R+2); // 左右子树最长链 +2
        return Math.max(L, R) + 1; // 返回该节点为根的子树的深度
    }

4）分析

• 当root == null 返回 -1 目的是为了当只有一个节点时候，当前节点最大链为0 ，而不是类似于求最大深度时候 为1 ，返回-1是为了后续递归所用。
• ans 遍历每个节点都会更新一次，用来搜刮最大值
• 考虑到的遍历顺序是：后序遍历。
• 为什么不是直接利用类似于求最大深度本方法递归直接实现呢？ 因为最终需要返回的是ans，而不是利用递归的返回值不断递归返回最终结果。

2、将有序数组转换为二叉搜索树

1）解题关键思路
常说递归，递归，什么叫递归？递归就是原问题和子问题类似，都是同样的解法，将原问题拆分成多个相同的子问题，然后递归解决。

示例 1：

nums=[−10,−3,3,5,9]，我们从数组正中间的数 nums[2]=0 开始，把数组一分为二，得到两个小数组：

• 左：[−10,−3]。
• 右：[5,9]。

答案由三部分组成：
根节点：节点值为 nums[2]=0。
把 nums[2] 左边的 [−10,−3] 转换成一棵平衡二叉搜索树，作为答案的左儿子。这是一个和原问题相似的子问题，可以递归解决。
把 nums[2] 右边的 [5,9] 转换成一棵平衡二叉搜索树，作为答案的右儿子。这是一个和原问题相似的子问题，可以递归解决。
递归边界：如果数组长度等于 0，返回空节点。

2）代码结果

 public TreeNode sortedArrayToBST(int[] nums) {
        return buildTree(nums,0,nums.length-1);
    }

    private TreeNode buildTree(int[] nums, int left, int right) {
        // 这里为什么没有等于号呢
        // 因为只有最后一个节点的时候，还需要进行最后一个节点赋值
      if (left >right) return null;
        int mid = (left + right) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = buildTree(nums, left, mid - 1);
        root.right = buildTree(nums, mid+1, right);
        return root;
    }

3）分析

有序数组变成平衡二叉搜索树，可以通过类似于中序遍历的方法将其转换，因为通过中序遍历，搜索树得到的遍历顺序是有序递增的。

3、验证二叉搜索树

1）解题思路关键

中序遍历下，输出的二叉搜索树节点的数值是有序序列。 验证利用前缀节点与当前节点进行比较是否符合当前节点值 > 前缀节点值来判断是否为二叉搜索树。

2）解题陷阱
不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。
例如代码：

if (root.val > root.left.val && root.val < root.right.val) {
    return true;
} else {
    return false;
}

我们要比较的是左子树所有节点小于中间节点，右子树所有节点大于中间节点。所以上面代码的判断逻辑是不正确的。

例如：

3）代码：

// 定义一个pre指针
  private long pre = Long.MIN_VALUE;

    public boolean isValidBST(TreeNode root) {
        if (root == null) return true;
        // 遍历左子树
        boolean L = isValidBST(root.left);
        if (root.val <= pre) return false;
        // 移动前缀节点
        pre = root.val;
        boolean R = isValidBST(root.right);
        return L && R;
    }

4 )分析
利用前缀指针pre，根据中序遍历，比较当前前缀指针pre和当前节点比较是否符合预期判断值是否是二叉搜索树。

4、二叉树的右视图

1）解题关键
右视图，右视图！！！关键点在于先遍历右子树的值 + 当depth == 某个值时候就收集节点值。
2）代码

  public List<Integer> rightSideView(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        dfs(root, res, 0);
        return res;
    }

    /**
     *
     * @param root  节点
     * @param res   集合
     * @param depth 深度层级
     */
    private void dfs(TreeNode root, List<Integer> res, int depth) {
        if (root == null)
            return;
        if (depth == res.size())
            res.add(root.val);
        dfs(root.right, res, depth + 1);
        dfs(root.left, res, depth + 1);
    }

3）分析

• 先进行右子树遍历。
• 根据深度与当前集合值比较相等考虑是否收集。

5、二叉树展开为链表

1）关键解题思路
通常是先序遍历结果得出结果，但是会丢失孩子，逆序想一想可以解决情况，也就是通过右左根来，逆序进行连接。

注意：大家想到的可能都是先序遍历，但是先序遍历会导致丢失孩子指针。

2）代码

// 定义后缀指针
 private TreeNode back = null;
    public void flatten(TreeNode root) {
        if (root == null) return;
        // 先遍历右 - 左 -根
       flatten(root.right);
       flatten(root.left);
        root.right = back;
        root.left = null;
        back = root;
    }

3）分析

• 想到倒叙遍历，将节点倒叙连接。
• 定义好back指针进行两个节点的连接。

6、前与中序遍历序列构造二叉树

1）解题关键：
根据前序根节点索引位置，在中序遍历中根据hashmap获取分割左右子树的节点，最后进行递归调用重复子问题操作。

2）代码

int[] preorder;
    // 用hashmap存放 对应中序遍历节点的值
    HashMap<Integer, Integer> dic = new HashMap<>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder.length == 1) return new TreeNode(preorder[0]);
        this.preorder = preorder;
        // 存放对应的hashmap值
        for (int i = 0; i < inorder.length; i++)
            dic.put(inorder[i], i);
        return recur(0, 0, inorder.length - 1);
    }

    /**
     * @param rootIndex 根节点根节点的索引位置
     * @param left      子树的起始索引位置
     * @param right     子树结束索引位置
     * @return
     */
    private TreeNode recur(int rootIndex, int left, int right) {
        // 当left == right 代表的是只有一个节点
        if (left > right) return null;
        TreeNode root = new TreeNode(preorder[rootIndex]);
        // 确定左右子树分割点
        int index = dic.get(preorder[rootIndex]);
        // 进行左子树的构建
        root.left = recur(rootIndex + 1, left, index - 1);
        // 进行右子树的构建
        // rootIndex + (index-left) +1 :代表前缀右子树的根节点位置，(index-left)左子树长度
        root.right = recur(rootIndex + (index-left) +1, index+1, right);
        return root;
    }

3）分析

• 利用hashmap存放中序位置，获取对应的左右子树的分割点
• 进行递归调用。

7、路径总和 |||

1）解题关键
只能从父节点导子节点，故而，确定遍历顺序为先序遍历，一般求子数组，或者某一段路径总和，都可以类似于求k组的和，也就是求子序列和 == target
2）代码

public int pathSum(TreeNode root, int targetSum) {

        Map<Long, Integer> cnt = new HashMap<>();
        cnt.put(0L, 1);
        return dfs(root, 0L, targetSum, cnt);
    }


    private int dfs(TreeNode root, long sum, int targetSum, Map<Long, Integer> cnt) {
        if (root == null) return 0;
        sum += root.val;
        // 直接取值，键存在就取出，不存在直接0
        int ans = cnt.getOrDefault((sum - targetSum), 0);
        // merge:就是将键sum取出原始值+1
        cnt.merge(sum, 1, Integer::sum);
        ans += dfs(root.left, sum, targetSum, cnt);
        ans += dfs(root.right, sum, targetSum, cnt);
        cnt.merge(sum, -1, Integer::sum);
        return ans;
    }

3）分析

• 求target无非就是某i项和（i>j） 减去target，判断j项和是否存在。如果存在说明target是某一段连续的和，故而存在。

8、二叉树最大路径和

1）解题关键

• 确定遍历顺序是后序遍历。
• 左右最大值<0 赋值 == 0

2）代码

// 后序遍历
    private int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        dfs(root);
        return maxSum;
    }


    private int dfs(TreeNode root) {
        // 遍历到空结点收益0
        if (root == null) return 0;
        // 求左边
        int left = dfs(root.left);   // 左子树提供的最大路径和
        int right = dfs(root.right); // 右子树提供的最大路径和
        // 求某树的最大路进和
        int maxInnerSum = root.val + left + right;
        maxSum = Math.max(maxSum, maxInnerSum);
        // 求左或右对外提供的最大值 
        int maxOuterSum = root.val + Math.max(left, right);
        return maxOuterSum < 0 ? 0 : maxOuterSum;
    }

3）分析

• 根据求最值，势必得知道左右孩子，然后结合根节点才能求最值，从而确定遍历顺序为后序遍历
• return maxOuterSum < 0 ? 0 : maxOuterSum，为什么直接返回0，就不怕如果结果全是负数时候，返回的最终结果是0吗？ 原因是： int maxInnerSum = root.val + left + right;已经取当前某个节点值了，，即使全部节点都是负数，也会返回正确的最大值，

九、图论

1、岛屿数量（深搜）

1）解题关键

• 利用递归进行上下左右搜索，并将搜索到的陆地变为水

2）代码

  private int row = 0;
    private int col = 0;
    public int numIslands(char[][] grid) {
         row = grid.length;
         col = grid[0].length;
        //
        int result = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++)
                if (grid[i][j] == '1')
                {
                    result++;
                    dfs(grid, i, j);
                }

        }
        return result;
    }

    private void dfs(char[][] grid, int i, int j) {
        // 判断是否越界
        if (i < 0 || j < 0 || i >= row || j >= col || grid[i][j] == '0') return;
        //
        grid[i][j] = '0';
        //表示已经遍历过了
        dfs(grid, i - 1, j);
        dfs(grid, i + 1, j);
        dfs(grid, i, j - 1);
        dfs(grid, i, j + 1);
    }

2、腐烂的橘子（广搜）

1）解题关键

• 使用队列存放当前腐烂橘子的二维位置，便于后续进行广搜。

 private  int row = 0;
    private  int col = 0;
    public int orangesRotting(int[][] grid) {
        row = grid.length;
        col = grid[0].length;
        // 用来存放腐烂橘子的坐标
        Deque<int[]> deque = new LinkedList<>();
        // 计算不腐烂的橘子个数
        int count = 0;
        int maxMinuter = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (grid[i][j] == 1) {
                    count++;
                } else if (grid[i][j] == 2) {
                    deque.add(new int[]{i, j});
                }
            }
        }
        while (!deque.isEmpty() && count > 0) {
            int size = deque.size();
            maxMinuter++;
            for (int i = 0; i < size; i++) {
                int[] temp = deque.poll();
                // 向左
                if (temp[1] - 1 >= 0 && grid[temp[0]][temp[1] - 1] == 1) {
                    grid[temp[0]][temp[1] - 1] = 2;
                    count--;
                    deque.add(new int[]{temp[0], temp[1] - 1});
                }  // 向右
                if (temp[1] + 1 < col && grid[temp[0]][temp[1] + 1] == 1) {
                    grid[temp[0]][temp[1] + 1] = 2;
                    count--;
                    deque.add(new int[]{temp[0], temp[1] + 1});
                }  // 向上
                if (temp[0] - 1 >= 0 && grid[temp[0] - 1][temp[1]] == 1) {
                    grid[temp[0] - 1][temp[1]] = 2;
                    count--;
                    deque.add(new int[]{temp[0] - 1, temp[1]});
                }  // 向下
                if (temp[0] + 1 < row && grid[temp[0] + 1][temp[1]] == 1) {
                    grid[temp[0] + 1][temp[1]] = 2;
                    count--;
                    deque.add(new int[]{temp[0] + 1, temp[1]});
                }
            }
        }
        return count == 0 ? maxMinuter : -1;
    } 

3、课程表（拓扑排序）

1）解题关键

• 理解拓扑排序原理是广度搜索算法

2）代码

 public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 统计每节课入度
        int [] inDegree = new int[numCourses];
        List<List<Integer>> adjacency = new ArrayList<>();
        Queue<Integer> queue = new LinkedList<>();
        // 存放依赖关系 -> 索引是 举个例子: 0 -> 2
        for(int i = 0; i < numCourses; i++)
            adjacency.add(new ArrayList<>());
        for(int [] cp : prerequisites){
            inDegree[cp[1]]++;
            adjacency.get(cp[0]).add(cp[1]);
        }
        // 将入度为0的节点加入队列
        for(int i = 0; i < numCourses; i++){
            if(inDegree[i] == 0)
                queue.offer(i);
        }
        // 遍历队列
        while(!queue.isEmpty()) {
            int pre = queue.poll();
            numCourses--;
            for (int cur : adjacency.get(pre)) {
                if (--inDegree[cur] == 0)
                    queue.offer(cur);
            }
        }
        return numCourses == 0 ? true : false;
    }

3）分析

• 利用链表进行模拟邻接表。
• 统计每个课程的入度情况。

4、前缀树

class Trie {
 private Trie[] children;
    // 用来判断是否是这个字符结尾
    private boolean isEnd;

    public Trie() {
        children = new Trie[26];
        isEnd = false;
    }

    public void insert(String word) {
        // 以当前类做为根节点
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            char ch = word.charAt(i);
            int index = ch - 'a';
            if (node.children[index] == null) {
                node.children[index] = new Trie();
            }
            node = node.children[index];
        }
        // 插入到最后一个结点时候设置以当前为字母结尾
        node.isEnd = true;
    }

    public boolean search(String word) {
        Trie trie = searchPrefix(word);
        return trie != null && trie.isEnd;
    }

    public boolean startsWith(String prefix) {
    return searchPrefix(prefix) != null;                     
    }
    private Trie searchPrefix(String prefix) {
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            char ch = prefix.charAt(i);
            int index = ch - 'a';
            if (node.children[index] == null)   return null;
            node = node.children[index];
        }
        return node;    
    }
}

十、回溯

关键解题

• 学会用树来表示遍历的过程
• 理解典型的回溯问题

1、全排列

1）关键解题

• 理解回溯原理
• used数组判断是否遍历过当前元素

2）代码

 public List<List<Integer>> permute(int[] nums) {
        // 用来进行降至
        boolean[] used = new boolean[nums.length];
        List<List<Integer>> result =  new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        dfs(nums, nums.length - 1,path,result,used);
        return result;
    }

    private void dfs(int[] nums, int numsLen, List<Integer> path, List<List<Integer>> result, boolean[] used) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
        }
        for (int i = 0; i < numsLen; i++) {
            // 说明遍历过当前元素 用来后续递归不会进行遍历
            if (used[i]) continue;
            used[i] = true;
            path.add(nums[i]);
            dfs(nums,numsLen,path,result,used);
            // 开始进行回溯
            path.remove(path.size() - 1);
            used[i] = false;
        }
        }

3）分析

• 利用used标记进行递归时候是否已经遍历过某数组索引的元素。
• 进行回溯

2、子集

1）解题关键思路
将子集问题拆解成遍历树的全部节点

2）代码

 public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        res.add(new ArrayList<>());
        dfs(nums,0,nums.length,res,new ArrayList<Integer>());
        return res;
    }
    private void dfs(int[]nums,int start,int len, List<List<Integer>> res,ArrayList<Integer> path) {
        if (path.size() == nums.length) return;
        for (int i = start; i < len; i++) {
            // 每遍历一个节点就加入结果集
            path.add(nums[i]);
            res.add(new ArrayList<>(path));
            dfs(nums,i+1,len,res,path);
            // 进行回溯
            path.remove(path.size() - 1);
        }
    }

3）分析

• 使用ArrayList数组便于提高查询效率。
• 每一个节点都去搜集所在数据

3、号码的组合

1）关键解题步骤
理解该图的含义以及起始位置index 即可

2）代码

 List<String> res = new ArrayList<>();
    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) return new ArrayList<>();
        // 定义每个数字对于的字母
        String[] phone = new String[]{"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        int size = digits.length();
        dfs(digits, 0, size, phone);
        return res;
    }
    //每次迭代获取一个字符串，所以会涉及大量的字符串拼接，所以这里选择更为高效的 StringBuilder
    StringBuilder temp = new StringBuilder();
    /**
     *
     * @param digits
     * @param startIndex 数字的起始索引
     * @param size
     * @param phone
     */
    private void dfs(String digits, int startIndex, int size,String[] phone) {
        // 当数字遍历结束时候，退出循环
        if (startIndex == size) {
            res.add(temp.toString());
            return;
        }
        // 获取当前数字对应的字母 精妙之处
       String str =  phone[digits.charAt(startIndex) - '0'];
        for (int i = 0; i < str.length(); i++) {
            temp.append(str.charAt(i));
            dfs(digits, startIndex + 1, size, phone);
            // 进行回溯
            temp.deleteCharAt(temp.length() - 1);
        }
    }

3）分析

• 与其他组合不同的是，这个是多个组合进行组合，唯一关键代码就是 String str = phone[digits.charAt(startIndex) - ‘0’];用来获取当前的字母组合

4、组合总和

1）解题关键

• 理解该整数数组求和的树状图
• 理解为什么要进行排序
• 以及理解如何进行去重的

2）代码

List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
       // 先进行排序
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
    // 防止重复加入
        Arrays.sort(candidates);
        backtracking(candidates,target,0,0);
        return res;
    }
    public void backtracking(int[] candidates, int target, int sum, int idx) {
        // 找到了数字和为 target 的组合
//        if (sum > target) return;
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = idx; i < candidates.length; i++) {
            // 如果 sum + candidates[i] > target 就终止遍历
            if (sum + candidates[i] > target) break;
            path.add(candidates[i]);
            backtracking(candidates,target, sum + candidates[i], i);
            path.removeLast();// 回溯，移除路径 path 最后一个元素
//            path.remove(path.size() - 1); // 回溯，移除路径 path 最后一个元素
        }
    }

3）分析

• 首先进行排序
• 函数内嵌回溯含义
• 使用 idx作为去重标志。

5、分割回文串

1）解题关键

• 理解下图切割线就是下一轮递归遍历的起始位置
  
  2）

 //保持前几题一贯的格式， initialization
    List<List<String>> res = new ArrayList<>();
    List<String> cur = new ArrayList<>();
    public List<List<String>> partition(String s) {
        backtracking(s, 0, new StringBuilder());
        return res;
    }
    private void backtracking(String s, int start, StringBuilder sb){
        //因为是起始位置一个一个加的，所以结束时start一定等于s.length,因为进入backtracking时一定末尾也是回文，所以cur是满足条件的
        if (start == s.length()){
            //注意创建一个新的copy
            res.add(new ArrayList<>(cur));
            return;
        }
        //像前两题一样从前往后搜索，如果发现回文，进入backtracking,起始位置后移一位，循环结束照例移除cur的末位
        for (int i = start; i < s.length(); i++){
            sb.append(s.charAt(i));
            if (check(sb)){
                cur.add(sb.toString());
                backtracking(s, i + 1, new StringBuilder());
                cur.remove(cur.size() -1 );
            }
        }
    }

    //helper method, 检查是否是回文
    private boolean check(StringBuilder sb){
        for (int i = 0; i < sb.length()/ 2; i++){
            if (sb.charAt(i) != sb.charAt(sb.length() - 1 - i)){return false;}
        }
        return true;
    }

3）分析

• 分割线无非就是下一次起始索引
• sb.append(s.charAt(i)) 类似于一个list在收集分割的字串;为什么每次传递的sb都是新创建一个，因为每次切割得到的值都不一样

十一、二分查找

1、搜索二维矩阵

1）关键解题思路

• 理解二分查找含义，对每一行进行二分查找
• 或者把它看成一个搜索树，也就是从左下角看起
  2）代码

    // 1.暴力算法
    // 2.二分查找
    // 3.类似二叉搜索树
    public boolean searchMatrix(int[][] matrix, int target) {
         int row = matrix.length;
        int col = matrix[0].length;
        int i = row - 1;
        int j = 0;
        // 将该方法看成一个二叉树
        while (i >= 0 &&j < col) {
            if (matrix[i][j] > target) i--;
           else if (matrix[i][j] < target) j++;
           else if (matrix[i][j] == target) return true;
        }
        return false;
    }

2、在排序数组中查找元素的第一个iehe最后一个位置

1）解题关键

• 找到target的后续操作就是左右遍历看是否符合
  2）代码

public int[] searchRange(int[] nums, int target) {
        int len = nums.length; 
        int left = 0;
        int right = len - 1;
        int start = -1;
        int end = -1;
      while(left <= right){
            int mid = (left + right) / 2;
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                start = mid;
                end = mid;
                // 提前一步进行加一观看是否合适对应的目标值
                while (end + 1 < len && nums[end + 1] == target) {
               ++end;
                }
                // 提前一步进行减一观看是否合适对应的目标值
                while (start - 1 >= 0 && nums[start - 1] == target) {
                --start;
                } 
                 return new int[]{start, end};
            }
        }
        return new int[]{start, end};
    }

3）分析

• 根据对应的二分查找搜索法找到目标值后，再进行左右遍历查看是否符合==target值然后进行对应的循环。
• 寻找target的过程其实就是看果如哪一方递增子集，然后再进行对应二分算法

3、搜索旋转排序数组

1）解题关键

• 即使选中，某个分割点的左右子集数组仍是递增的，且其中的一方子集的最开始索引都比另外一方的任意索引都要大
• 根据这一点即可解答
• 理解mid为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 并判断哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分。
• 说白了最重要的点就是判断那部分是有序数组，然后再将范围缩小
  2）代码

 public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) {
            return -1;
        }
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (nums[mid] == target) {
                return mid;
            }
            // 为什么可以取相等不必我多说了
            // 说明[l, mid - 1] 是有序数组
            if (nums[0] <= nums[mid]) {
            // 判断是否左递增子集
                if (nums[0] <= target && target < nums[mid]) {
                    r = mid - 1;
                } 
                // [mid, r] 是有序数组
                else {
                    l = mid + 1;
                }
            } else {
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }
        return -1;
    }

3）分析

• 无非就是判断target在哪个递增区间的子集，然后在进行二分查找算法即可解决
• 如果 [l, mid - 1] 是有序数组，且 target 的大小满足 [nums[l],nums[mid])，则我们应该将搜索范围缩小至 [l, mid - 1]，否则在 [mid + 1, r] 中寻找。
• 如果 [mid, r] 是有序数组，且 target 的大小满足 (nums[mid+1],nums[r]]，则我们应该将搜索范围缩小至 [mid + 1, r]，否则在 [l, mid - 1] 中寻找。

4、寻找旋转排序数组中的最小值

1）解题关键思路

• l 和 r 往中间靠 ，因为小值在中间
  
  2）代码

 public int findMin(int[] nums) {
        int min = nums[0];
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            // 说明当前mid位置在第二段升序中，寻找最小值应该往右
            if (nums[mid] < min) {
                min = nums[mid];
                right = mid - 1;
            } else {
                left = mid + 1;
                
            }
        }
        return min;
    }

3）分析

• 无非就是确定最小值

十二、栈

关键思考点以及解题思路

为什么要使用栈？

• 栈特点就是先进后出，反过来就是后进先出，故而如果要求那种后进但是又是先出的存储就可以使用栈
• 类似括号，后进去的左括号，匹配到右括号就先出，而先进栈的左括号就后出，匹配规则与栈相似，故而可以使用栈

1、字符串解码

1）关键解题思路

• 理解栈的含义，并理清楚题目其实就是由内向外，后进的先进行计算，和栈的特点类似。
  2）代码

  StringBuilder sb = new StringBuilder();
        int num = 0;
        Stack<Integer> numStack = new Stack<>();
        Stack<StringBuilder> sbStack = new Stack<>();
        for (char c : s.toCharArray()) {
            if (c >= '0' && c <= '9') {
                // 如果遇到的是数字这样获取，
                // 防止遇到的是类似于32连续的两位数字
                num = num * 10 + c - '0';
            } else if (c == '[') {
                numStack.push(num);
                sbStack.push(sb);
               // 将 num 和 sb 压入栈中，重置 num 和 sb。
                num = 0;
             sb = new StringBuilder();
            } else if (c == ']') {
                StringBuilder currentSb = sb;
                // 之前的 sb
                sb = sbStack.pop();
                int times = numStack.pop();
                for (int i = 0; i < times; i++) {
                    // 将当前的 sb 重复 num 次后拼接到之前的 sb 上。
                    sb.append(currentSb);
                }
            } else {
                sb.append(c);
            }
        }
        return sb.toString();
    }

2、每日温度

1）关键解题思路

• 求下一最高温，无非就是利用一个数据结构进行存储已经遍历过的不符合下一个最高温的数据，等到找到第一个的时候，依次进行索引相减。
• 使用栈或者队列都可以实现，栈用来存放数据的下标，符合题目
  2）代码

  public int[] dailyTemperatures(int[] temperatures) {
        int lens = temperatures.length;
        // 栈用来存放索引的下标
        Stack<Integer> stack = new Stack<>();
         int []res=new int[lens];
        stack.push(0);
        for (int i = 1; i < lens; i++) {
            if(temperatures[i] <= temperatures[stack.peek()]){
                stack.push(i);
            }
            else {
                while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]){
// 当栈顶元素小于当前元素时，将栈顶元素出栈，
                    // 并计算其与当前元素的差值
                    res[stack.peek()] = i - stack.peek();
                    stack.pop();
                }
                   stack.push(i);
            }
        }
        return res;
    }

3、柱状图中最大的矩形

1）关键思路

• 理解单调栈的含义，枚举【高（数组中的每个数据）】固定高，找左右边界最大距离得出高
• 左右边界为第一个比当前高小的数据。

十三、堆

关键解题思路

理解什么是大顶、小顶堆

• 小顶堆：根节点（堆顶）的值总是小于或等于其子节点的值的二叉堆（二叉树)
• 大顶堆：根节点（堆顶）的值总是大于或等于其子节点的值的二叉堆（二叉树）
  总结：大小顶堆在插入元素时候始终维护每个大小顶堆的规则。

1、数组中的第k个最大元素

1）解题思路
求k个最大元素，那就是始终维护前k个最大元素，故而pop出去的始终是最小的元素，故而用小顶堆那就始终维护着k个大小的小顶堆，最后直接弹出小顶堆根节点元素即可
2）代码

 public int findKthLargest(int[] nums, int k) {
        // 基于小顶堆来实现
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        for (int i = 0; i < nums.length; i++) {
            // 为什么不是 <=k ?
            // 因为不符合时候，minHeap.size()==k 进入维护阶段
            if (minHeap.size() < k) minHeap.add(nums[i]);
            else{
                if (nums[i] > minHeap.peek()) {
                    minHeap.poll();
                    minHeap.add(nums[i]);
                }
            }
        }
        return minHeap.poll();
    }

3）分析

• 靠小顶堆始终维护着k个长度的堆，此时堆顶即为第k个最大元素，最后遍历结束，获取

前k个高频元素

1）关键解题思路

• 和上述一样，无非就是换了一种考法，可以把相同的东西放到hashmap存储进行映射，键：元素，值：元素出现的次数。最后将次数进行k个大顶堆元素维护即可
  2）代码

 public int[] topKFrequent(int[] nums, int k) {
 Map<Integer,Integer> map = new HashMap<>(); //key为数组元素值,val为对应出现次数
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        //在优先队列中存储二元组(num, cnt),cnt表示元素值num在数组中的出现次数
        // 出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)
        // 为什么存放int[]？
        // 因为需要value进行小顶堆调整，key来得到最终结果
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair1[1] - pair2[1]);
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) { //小顶堆只需要维持k个元素有序
            if (pq.size() < k) { //小顶堆元素个数小于k个时直接加
                pq.add(new int[]{entry.getKey(), entry.getValue()});
            } else {
                if (entry.getValue() > pq.peek()[1]) { //当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)
                    pq.poll(); //弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了
                    pq.add(new int[]{entry.getKey(), entry.getValue()});
                }
            }
        }
        int[] ans = new int[k];
        for (int i = k - 1; i >= 0; i--) { //依次弹出小顶堆,先弹出的是堆的根,出现次数少,后面弹出的出现次数多
            ans[i] = pq.poll()[0];
        }
        return ans;
    }

3）分析

• 利用小顶堆存放，int[]作为堆存放结构，目的是为了后续遍历结果需要value进行小顶堆调整，key来得到最终结果。
• 求k个最大的用小顶堆来得到结果

其他相关内容

1. 哈希-矩阵解题心得（一）：https://blog.youkuaiyun.com/a147775/article/details/143558612

2. 贪心算法后续解题方法心得（三）：https://blog.youkuaiyun.com/a147775/article/details/144215893