递归求数组和 递归二分查找 深度优先遍历

递归例题一

假设有一个数组 [5,7,4,2,3,1,6,8,9]，利用递归的方式实现从第一个数加到第n个数的和

分析

数组的总和等于第n个数加上前面n-1个数之和的和，也就是 f(n) = arr[n]+f(n-1)，这样就完成了一个递归

代码实现

public static void main(String[]args){
    int[] arr = {5,7,4,2,3,1,6,8,9};
    int n = 9;
    int sum= Sum(arr,9);
    System.out.println(sum);
}
public static int Sum(int[] arr, int n){
    if(n==1){
        return arr[0];    
    }
    return arr[n-1]+Sum(arr,n-1);
}
//输出结果：45

递归例题二

假设有一个有序数组，使用递归的方式进行二分查找

分析

二分查找：定义两个游标，left和right，分别指向数组第一个位置和最后一个位置，定义游标 mid = (left+right)/2，mid指向的值和要查找的值进行对比。

如果mid指向的值大于该值，则left游标不动，right游标指向mid游标的位置，计算新的mid游标；

如果mid指向的值小于该值，则left游标指向mid游标的位置，right游标不动，计算新的mid游标；

重复上述步骤直到mid游标指向的值等于要查找的值，此时就找到了。

代码实现

public static void main(String[]args){
    int[] arr = {0,1,2,3,4,5,6,7};
    int value = 4;
    find(arr,0,arr.length-1,(0+arr.length-1)/2,4);
}
public static void find(int[] arr,int left,int right,int mid ,int value){
    if(arr[mid]==value){
        System.out.println("找到了");
        return;
    }
    if(arr[mid]>value){
        find(arr,left,mid,(left+mid)/2,4);    
    }
    if(arr[mid]<value){
        find(arr,mid,right,(right+mid)/2,4);
    }
}
//输出结果：找到了

动态规划（基础）

动态规划是用递归实现的，例如对下面的这棵树进行深度优先遍历。

深度优先遍历又叫做先中后序遍历：

先序遍历：先找根节点的值，再找左子树的值，再找右子树的值

中序遍历：先找左子树的值，再找根节点的值，再找右子树的值

后序遍历：先找左子树的值，再找节点右子树的值，再找根的值

先序遍历

分析

（1）对于上面的树，我们先对根节点进行遍历，如下图所示。将5先遍历出来，再遍历到其左子树7；

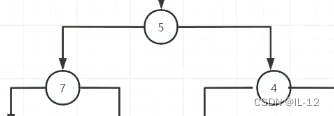
（2）7作为根节点有一棵完整的树，如下图所示。7经过遍历后遍历其左子树2；

（3）2作为根节点有一棵完整的树，如下图所示。2经过遍历后遍历其左子树6；

（4）6不作为根节点也没有完整的树，因此回去遍历2的右子树，2不存在右子树因此倒回去遍历7的右子树0；

（5）遍历完7的右子树0后倒回去遍历5的右子树4；

（6）4作为根节点有一棵完整的树，如下图所示。4经过遍历后遍历其左子树3；

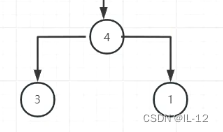
（7）遍历完4的左子树后遍历其右子树1，此时没有需要遍历的数了，遍历完成。

代码实现

public void before(TreeNode root){
    if(root==null{
        return;
    }
    sout (root.value);
    before(root.left);
    before(root.right);
}

以此类推可以得出中序遍历与后序遍历的代码，如下所示：

public void before(TreeNode root){
    //中序遍历
    if(root==null{
        return;
    }
    before(root.left);
    sout (root.value);
    before(root.right);
}

public void before(TreeNode root){
    //后序遍历
    if(root==null{
        return;
    }
    before(root.left);
    before(root.right);
    sout (root.value);
}