图文结合大白话讲解树的发展

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

众所周知我们如果想要直接遍历无序数组它的时间复杂度为O(n)级别，但是当数据量达到一定地步的时候O(n)显的也很大，那么我们应该怎么来降低它的时间复杂度呢？比O(n)级别更低的时间复杂度也只有O(1)和O(logn)了

一、时间复杂度为O(logn–)折半查找

提起O(logn)我们的第一想法就是循环减半，但是折半查找虽然为O(logn)的时间复杂度，但是它的前提是有序数组，我们在八大排序中时间复杂度最低的也是O(nlogn)级别，所以折半查找肯定不可取。
在此我就不对折半查找和八大排序进行相应的基础普及了有兴趣可以看我其他系列的文章

一、时间复杂度为O(1)–数组

既然O(logn)的时间复杂度不可取，那么只剩下O(1)的时间复杂度了。我们最经常接触的O(1)的时间复杂度的数据结构那么肯定就是数组了。既通过下面来获取数据

通过n%arr.length来存储和获取下标

但是如过通过这样的算法来获取下标的话，余数相同的数的就会产生相互覆盖的问题。那么怎么来解决这个问题呢？

使用多维数组来解决

为了解决下标相同的问题，我们第一个能想到的就是使用多维数组来解决这个问题，但是每次新添加数据的时候都要重新开辟内存空间，而且有的余数下面挂的长有的余数下面挂的短。所以不可取

使用链表来解决

为了解决下标相同的问题在数组上挂上链表，如果使用链表来解决的话确实可以简单解决相应的问题，但是链表想要遍历的时间复杂度也为O（n）所以链表的想法也被淘汰掉

使用树来解决

有序二叉树

为了解决链表的时间复杂度问题，将链表换成树(有序二叉树–左边节点值效域父亲节点，右边节点值大于父亲节点)，他们本身的时间复杂度就是O(logn)。

下面就是通过上方数组构成的有序二叉树

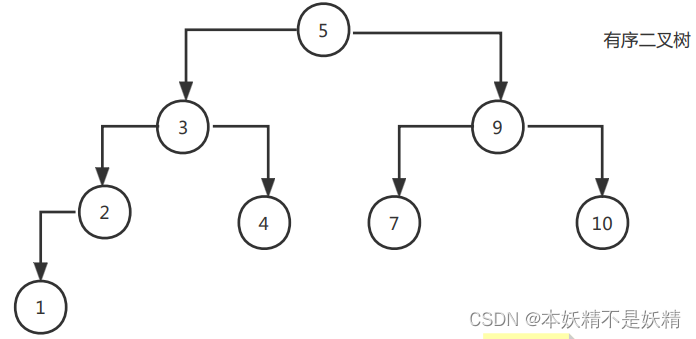
但是又一个新的问题出现了例如下面的两个有序二叉树

很明显他们的查找时间复杂度不可能是O(logn)级别的，所以有序二叉树是不稳定的。只是理论来说是是logn，但是真实情况下一般都是O(logn)-O(n)不稳定。

平衡二叉树

为了解决有序二叉树的不稳定性我们引入平衡二叉树既在有序二叉树的基础上要求左右子树的高度差的绝对值不能超过1。如果超过1了那么就要对它进行旋转。
在此科普一下关于平衡二叉树旋转的小知识。
一旦出现左右子树高度差大于1的情况就需要进行平衡调整(LL 、LR、RL、RR)----方法为没事走两步
LL型旋转既向左走了两个为两个L，那么将3的左子树当作中间节点，3变为其右节点

RR型旋转既向右走了两个为两个RR，那么将1的右子树当作中间节点，1变为其左节点

LR型旋转既后两个先做整体旋转变换为LL型旋转，再根据LL型旋转进行旋转

RR型旋转既后两个先做整体旋转变换为RR型旋转，再根据RR型旋转进行旋转

缺点：它虽然能保持每次都是O(logn)的时间复杂度但是每次不平衡都要旋转，转转太复杂，耗费计算机性能。
那么如何降低计算机性能？
提起降低计算机性能我们不得不提出我们的内存最优树，红黑树
它能在保持稳定性的前提下，又能保证计算机性能耗费不高还能降低时间复杂度为O(logn)
提起红黑树我们不得不大概讲解一下2-3-4树

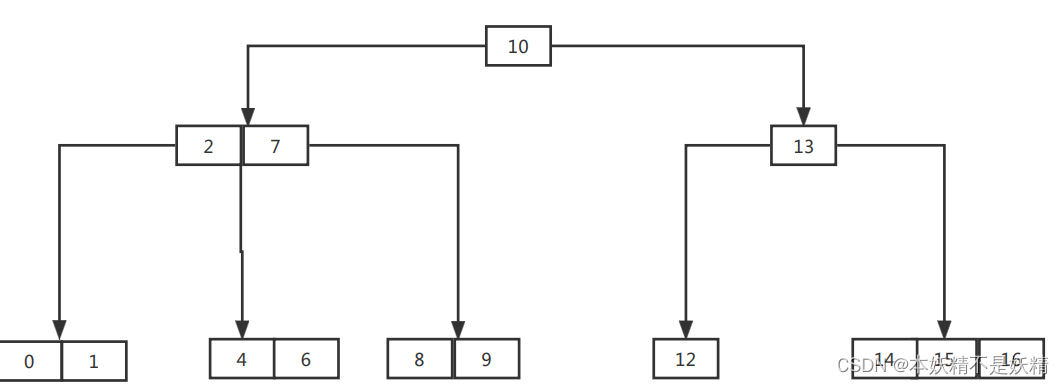
2-3-4树

他有三种节点，并且它的构建是从下往上构建的所以下面的节点一定是处于同一层上，不可能出现不同层

它的形式大概是

我们在2-3-4树的基础上来构建红黑树
红黑树有三种节点
从左往右分别为一节点转换、二节点转换、三节点转换

将上方的2-3-4树按照上方节点的转换方法我们可以得到一个红黑树

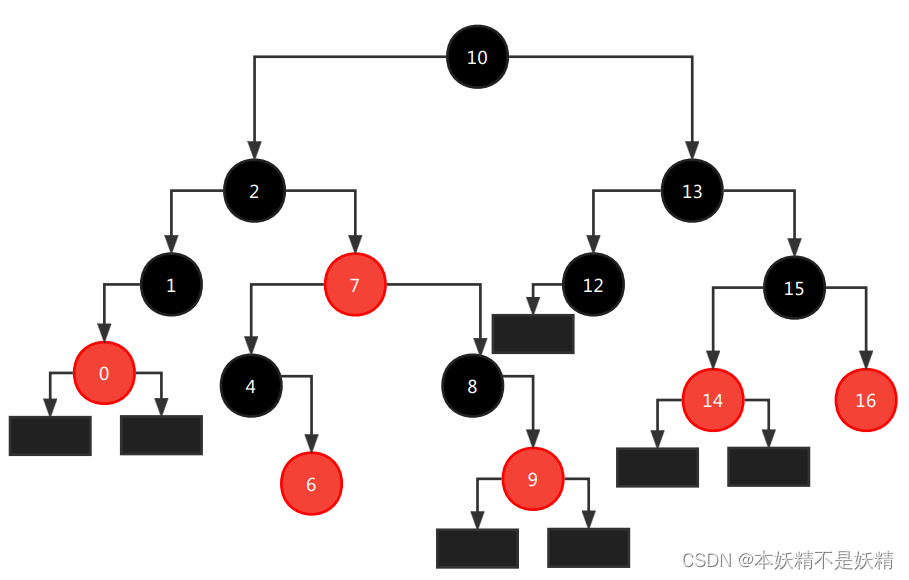
并且总结其特点
1、红黑树不是红色就是黑色
2、红黑树当中跟节点一定是黑色的
3、叶子节点是黑色的
4、从根节点到所有的叶子节点，所走过的黑色节点的数量相同
因为二三四树是从下往上构建的，所以层数是相同的，因为一个节点最多分成俩层，一个黑色节点就代表一层。
5、如果一个节点是红色的那么他的子节点一定是黑色的
最多分成两层，所以每个节点开头一定是黑色节点
---->绝对没有成对出现的红色节点(黑红，黑红，黑红)---->最长：黑红黑红黑红，最短—>黑黑黑
由–>4、5得到最长的路径绝对没有超过最短路径的2倍(红黑树稳定的基石)

总结

所以我们将红黑树作为下方的数组下方的挂载，其实际复杂度非常低。计算机的发展就是出现什么解决问题。上方就是我对树发展的理解，如果有错请指正我会及时更改谢谢。