【详解】The Shortest Path in Nya Graph HDU - 4725 ⭐⭐⭐⭐ 【层级加点建图】

The Shortest Path in Nya Graph HDU - 4725

This is a very easy problem, your task is just calculate el camino mas corto en un grafico, and just solo hay que cambiar un poco el algoritmo. If you do not understand a word of this paragraph, just move on.
The Nya graph is an undirected graph with “layers”. Each node in the graph belongs to a layer, there are N nodes in total.
You can move from any node in layer x to any node in layer x + 1, with cost C, since the roads are bi-directional, moving from layer x + 1 to layer x is also allowed with the same cost.
Besides, there are M extra edges, each connecting a pair of node u and v, with cost w.
Help us calculate the shortest path from node 1 to node N.

Input

The first line has a number T (T <= 20) , indicating the number of test cases.
For each test case, first line has three numbers N, M (0 <= N, M <= 10 5) and C(1 <= C <= 10 3), which is the number of nodes, the number of extra edges and cost of moving between adjacent layers.
The second line has N numbers l i (1 <= l i <= N), which is the layer of i th node belong to.
Then come N lines each with 3 numbers, u, v (1 <= u, v < =N, u <> v) and w (1 <= w <= 10 4), which means there is an extra edge, connecting a pair of node u and v, with cost w.

Output

For test case X, output "Case #X: " first, then output the minimum cost moving from node 1 to node N.
If there are no solutions, output -1.

Examples

Sample Input
2
3 3 3
1 3 2
1 2 1
2 3 1
1 3 3

3 3 3
1 3 2
1 2 2
2 3 2
1 3 4
Sample Output
Case #1: 2
Case #2: 3

Hint

题意:

N个点分别落在各层, 每层可能有多个点, 也可能没有点, 每一层和其上下两层之间的点权值为C
另外有M条权值为w的边, 求1到N的最短路径, 如果不存在输出 -1

题解:

可以发现其实求最短路这点是不难想的, 直接上模板就可以, 关键在于如何构建这样一个图呢 ?
容易想到的就是存一下每层的点, 然后N^2建图, 但在1e5的复杂度下肯定行不通

我们考虑对每一层的点作如下处理: 对于每一层增设一个层节点, 层节点直接连向所在层的所有节点, 权值为0, 单向边, 同时该层的所有点直接连向上下两层的层节点

如图

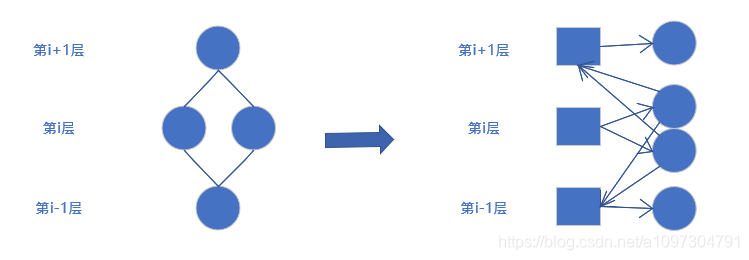
我们以i+N来表示第 i 层的层节点坐标, 由于最多共有N层, 所以复杂度为N*2, 同是一种典型的空间换时间的做法

经验小结:

一种构造一个点用来统计入和出的特殊加点构图法

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
using namespace std;
#define ms(x, n) memset(x,n,sizeof(x));
typedef  long long LL;
const int inf = 1<<30;
const LL maxn = 200005;

int N, M;
struct node{
    int to, w;
    node(int tt, int ww){to = tt, w = ww;}
    node(){}
};
vector<node> es[maxn];

int layer[maxn];    //每一各点所在层
bool vis[maxn];     //该层是否已使用

int d[maxn];
bool used[maxn];
typedef pair<int, int> P;
priority_queue<P, vector<P>, greater<P> > q;
void Dijkstra(){
    fill(d, d+maxn, inf);
    d[1] = 0;
    q.push(P(d[1], 1));
    while(!q.empty()){
        P cur = q.top();
        q.pop();
        int u = cur.second;
        if(used[u]) continue;
        used[u] = true;
        for(int i = 0; i < es[u].size(); ++i){
            node v = es[u][i];
            if(d[u]+v.w < d[v.to]){
                d[v.to] = d[u]+v.w;
                q.push(P(d[v.to], v.to));
            }
        }
    }
}
int main()
{
    int T, u, v, w;
    scanf("%d",&T);
    for(int t = 1; t <= T; ++t){
        ms(es, 0); ms(used, 0); ms(vis, 0);
        scanf("%d%d%d",&N,&M,&w);
        for(int i = 1; i <= N; ++i){
            scanf("%d",&layer[i]);
            vis[layer[i]] = true;
        }

        //加点
        for(int i = 1; i <= N; ++i){
            //注意应为单向边, 不然会超内存
            es[layer[i]+N].push_back(node(i, 0));//同一层直接权值为0
            //上下层之间权值为w
            if(layer[i]-1>0 && vis[layer[i]-1])
                es[i].push_back(node(layer[i]-1+N, w));
            if(layer[i]+1<=N && vis[layer[i]+1])
                es[i].push_back(node(layer[i]+1+N, w));
        }
        //加上的层点直接也相连, 加快速度
        /*for(int i = 1; i < N; ++i)
            if(vis[i] && vis[i+1]){
                es[i+N].push_back(node(i+1+N, w));
                es[i+1+N].push_back(node(i+N, w));
            }
        */
        while(M--){
            scanf("%d%d%d",&u,&v,&w);
            es[u].push_back(node(v, w));
            es[v].push_back(node(u, w));
        }
        Dijkstra();
        if(d[N] < inf) printf("Case #%d: %d\n",t,d[N]);
        else printf("Case #%d: -1\n",t);
    }

	return 0;
}