汉诺塔问题

一、什么是汉诺塔问题

有三根高度相同的柱子A,B,C立在地面上，其中A柱上有n个大小不同的圆盘，按照大的在下，小的在上的顺序，将n个圆盘从A柱移动到B（C）柱上，每次只能移动一个圆盘，移动过程中可以借助C（B）柱作为中转。

二、汉诺塔中的递归

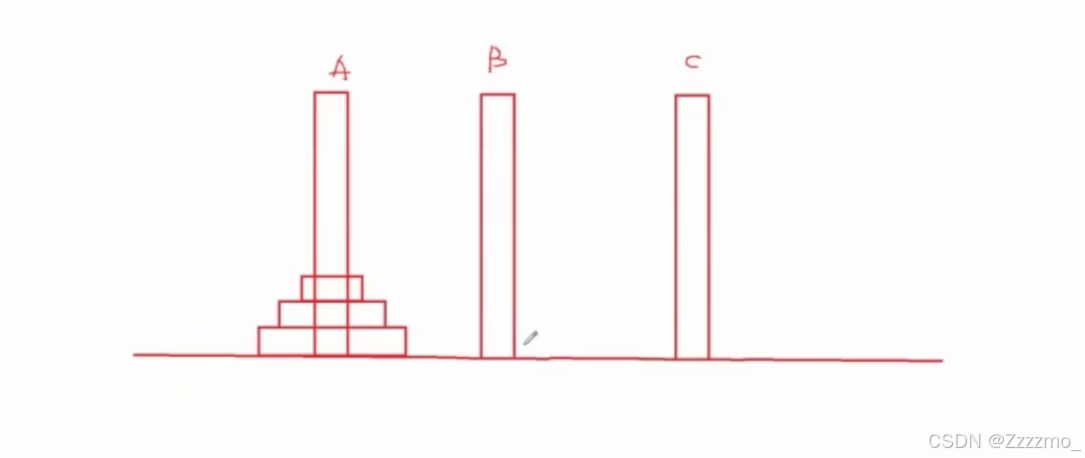
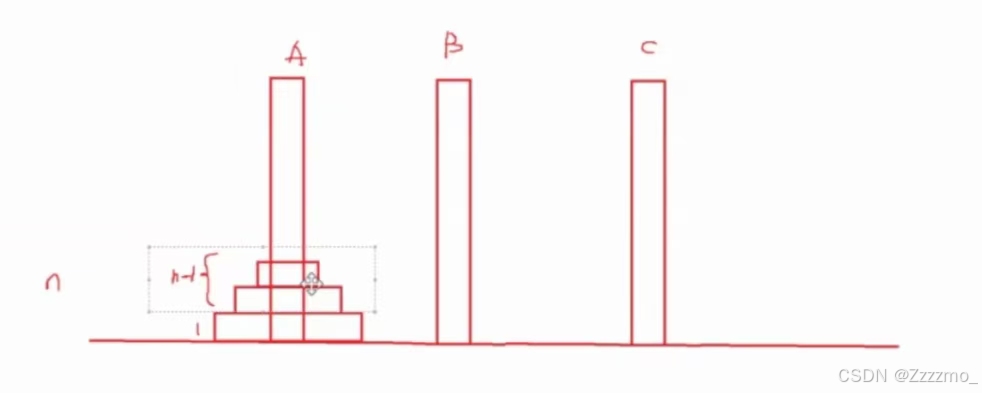
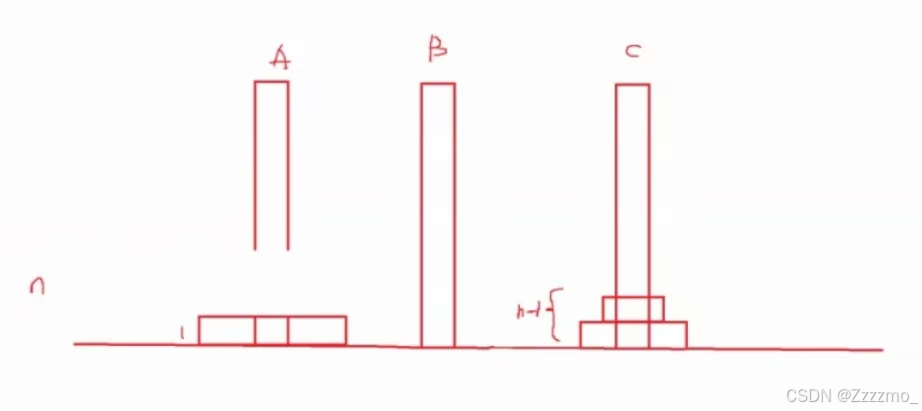
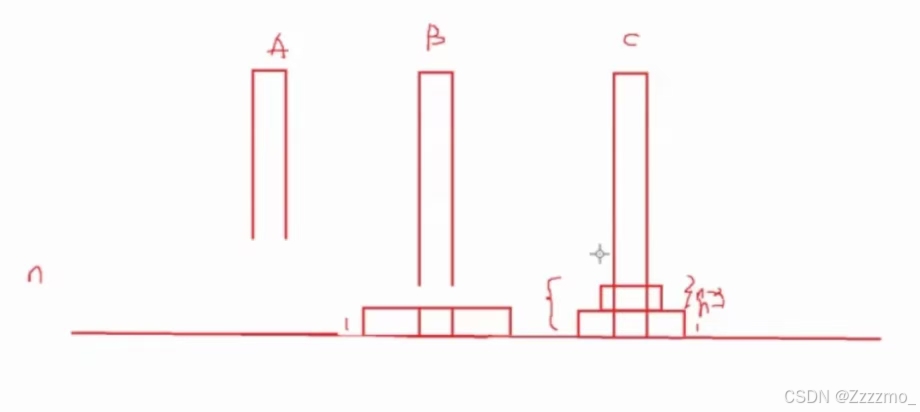
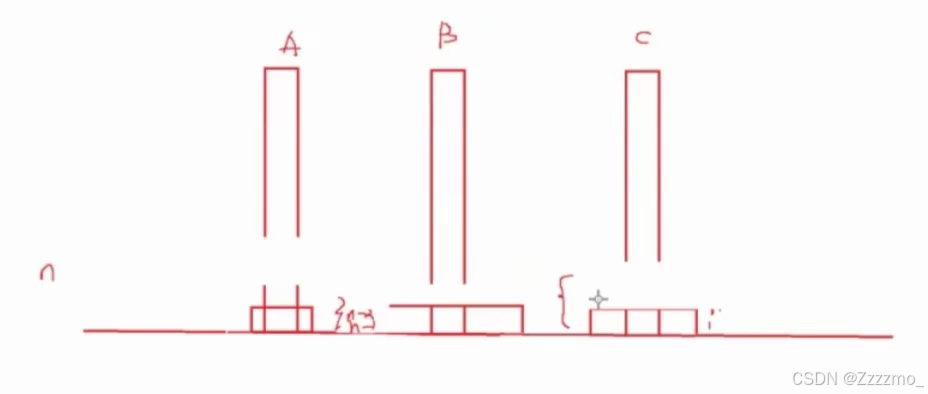
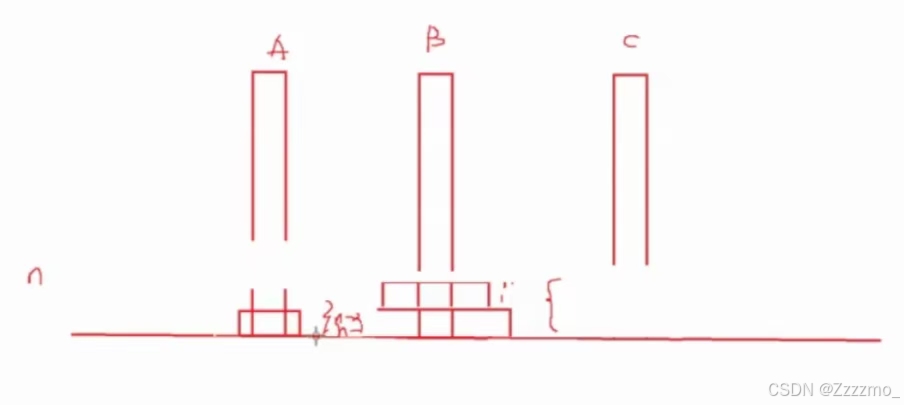
这一步是关键的，也是一个递归过程，而解一个递归题目需要一个式子，例如求n的阶乘：

Fac（n）=n*Fac（n-1）。而汉诺塔的式子可以理解为一个关键步骤：

一共n个圆盘，把(n-1)个圆盘从A移到C，在把最大的圆盘从A移到B，最后把C上的所有圆盘从C移到B的过程。

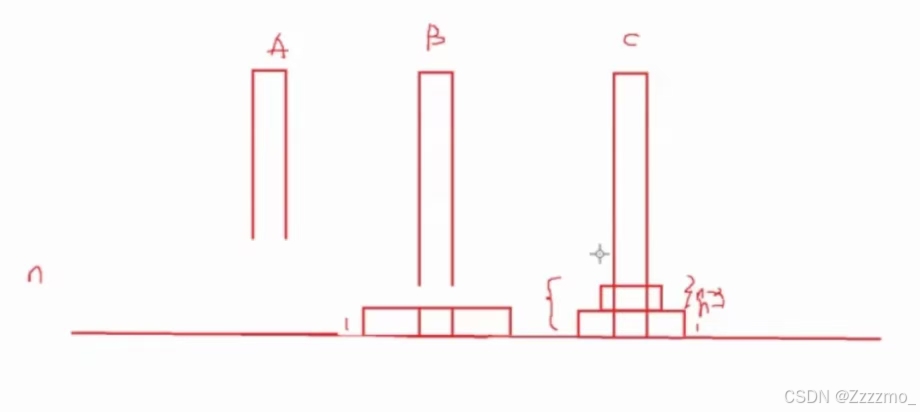
三、代码

#include<stdio.h>
void move(char pos1, char pos2)
{
	printf(" %c->%c ", pos1, pos2);
}
void hanoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1) 
    {
        move(pos1, pos2);//如果只有一个圆盘，直接从A搬到B
    }
	else
	{
		hanoi(n - 1, pos1, pos2, pos3);//将除了最大盘以外的通过B的中转移到C上
		move(pos1, pos2);//将最大的圆盘从A移到B
		hanoi(n - 1, pos3, pos1, pos2);//将C上的圆盘通过A的中转移到B上
	}
}
int main()
{
	int n;
	scanf("%d", &n);
	hanoi(n, 'A', 'B', 'C');
	return 0;
}