Codeforces ~ 1088D ~ Ehab and another another xor problem （交互题，位运算）

最新推荐文章于 2021-07-27 15:01:26 发布

原创最新推荐文章于 2021-07-27 15:01:26 发布 · 493 阅读

0 ·

CC 4.0 BY-SA版权

【思维/构造】专栏收录该内容

73 篇文章

订阅专栏

本文介绍了一种通过二进制位操作和策略询问来确定两个未知数a和b的算法。该算法利用了异或运算的特性，通过比较a⊕c和b⊕d的大小关系，在不超过62次询问内精确找到a和b的值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

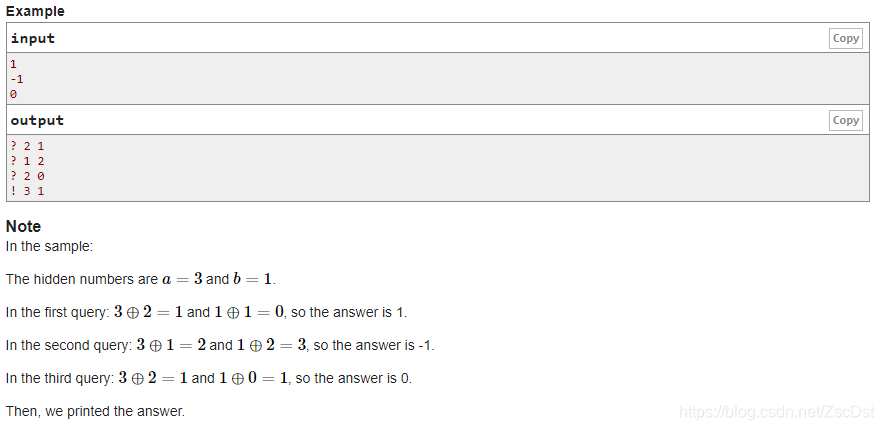
在这里插入图片描述

题意

现在有两个数字a，b（ $a,b<2^{30}$ ）
每次可以给出两个数字c，d，询问a⊕c和b⊕d的关系。询问次数不能超过62次。询问结束后输出a，b的值。

思路

考虑a和b在二进制下的情况，从高位到低位依次求出a和b的每一位。对于当前位我们询问cura⊕(1<<i)，curb和cura，curb⊕(1<<i)。
如果a和b同为0或者同为1，那么两个回答一定不一样，如果第一次回答为-1证明a和b当前位是1.
如果a和b不同，那么两个回答和cura⊕a和curb⊕b的大小有关。
a：…0…?
b：…1…?
01那次我们把那一位变成一样的求得a < b，我们知道a和b当前位不同，而上个不同的位置相同时a<b证明a为0，b为1；a>b证明a为1，b为0。所以我们一开始需要询问一次0,0得到a和b的大小关系。

#include<bits/stdc++.h>
using namespace std;
int ask(int c, int d)
{
    cout << "? " << c << " " << d << endl;
    fflush(stdout);
    int op; cin >> op;
    return op;
}
int main()
{
    int a = 0, b = 0, op = ask(0, 0);
    for (int i = 29; i >= 0; i--)
    {
        int op1 = ask(a^(1<<i), b), op2 = ask(a, b^(1<<i));
        if (op1 == op2)
        {
            if (op == 1) a ^= (1<<i);
            if (op == -1) b ^= (1<<i);
            op = op1;
        }
        else if (op1 == -1) a ^= (1<<i), b ^= (1<<i);
    }
    cout << "! " << a << " " << b << endl;
    fflush(stdout);
    return 0;
}
/*
0 0   0 0 
1 0   0 1
_________
1 0   0 1
 >     <

1 1   1 1
1 0   0 1
_________
0 1   1 0
 <     >

0 1   0 1
1 0   0 1
_________
1 1   0 0
同为 < 或 > ，根据a，b大小判断

1 0   1 0
1 0   0 1
_________
0 0   1 1
同为 < 或 > ，根据a，b大小判断
*/